Lcm Of 16 And 22
saludintensiva
Sep 20, 2025 · 6 min read
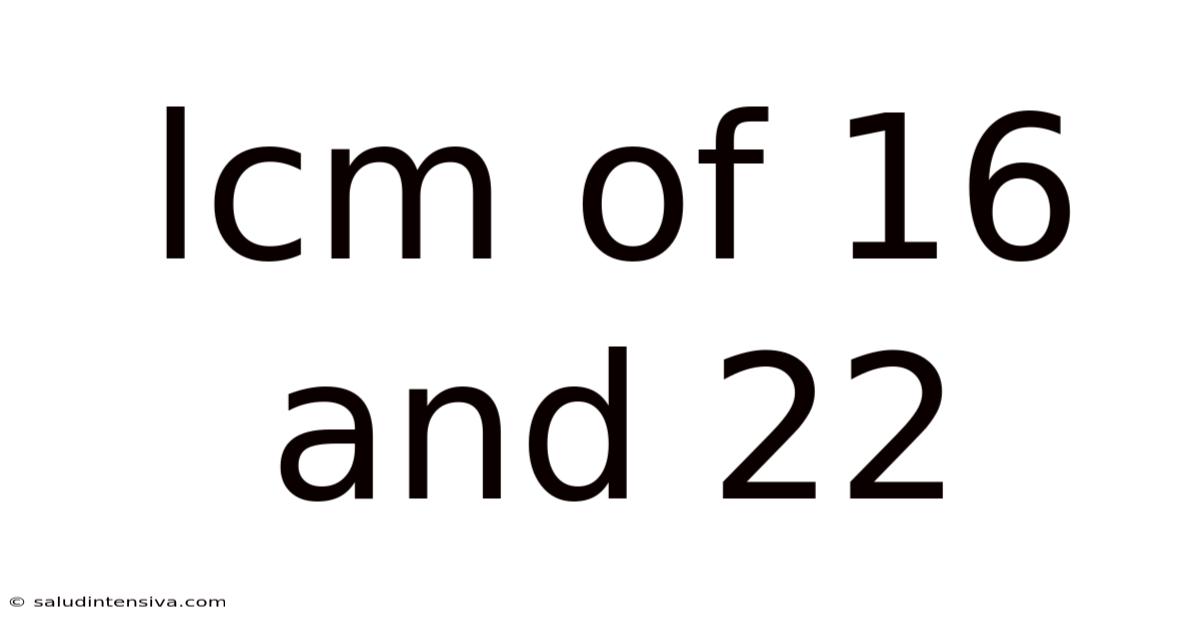
Table of Contents
Finding the Least Common Multiple (LCM) of 16 and 22: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can significantly enhance your mathematical understanding. This comprehensive guide will delve into the process of calculating the LCM of 16 and 22, exploring various approaches and providing a deeper insight into the concept of LCMs. We'll also address frequently asked questions to solidify your grasp of this fundamental mathematical concept.
Understanding Least Common Multiples (LCMs)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the prime factors of the original numbers. Understanding LCMs is crucial in various mathematical applications, including simplifying fractions, solving problems involving time intervals, and working with periodic phenomena.
Methods for Finding the LCM of 16 and 22
Several methods can be used to determine the LCM of 16 and 22. We'll examine three common approaches: the listing method, the prime factorization method, and the greatest common divisor (GCD) method.
1. The Listing Method:
This method involves listing the multiples of each number until a common multiple is found. While straightforward, it can be time-consuming for larger numbers.
-
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320, 336, 352, 368, 384, 400, 416, 432, 448, 464, 480, 496, 512, 528, 544, 560, 576, 592, 608, 624, 640, 656, 672, 688, 704...
-
Multiples of 22: 22, 44, 66, 88, 110, 132, 154, 176, 198, 220, 242, 264, 286, 308, 330, 352, 374, 396, 418, 440...
Notice that 176 is the smallest multiple common to both lists. Therefore, using the listing method, the LCM(16, 22) = 176. As you can see, this method becomes increasingly cumbersome with larger numbers.
2. The Prime Factorization Method:
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all the prime factors present.
-
Prime factorization of 16: 16 = 2 x 2 x 2 x 2 = 2<sup>4</sup>
-
Prime factorization of 22: 22 = 2 x 11
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2<sup>4</sup> = 16
- The highest power of 11 is 11<sup>1</sup> = 11
Therefore, LCM(16, 22) = 2<sup>4</sup> x 11 = 16 x 11 = 176
3. The Greatest Common Divisor (GCD) Method:
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula relating LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 16 and 22. We can use the Euclidean algorithm for this:
- Divide the larger number (22) by the smaller number (16): 22 = 16 x 1 + 6
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (6): 16 = 6 x 2 + 4
- Repeat: 6 = 4 x 1 + 2
- Repeat: 4 = 2 x 2 + 0
The last non-zero remainder is the GCD, which is 2.
Now, we can use the formula:
LCM(16, 22) x GCD(16, 22) = 16 x 22 LCM(16, 22) x 2 = 352 LCM(16, 22) = 352 / 2 = 176
Therefore, using the GCD method, the LCM(16, 22) = 176.
Choosing the Best Method:
The prime factorization method is generally preferred for its efficiency and clarity, particularly when dealing with larger numbers or multiple numbers. The listing method is suitable only for smaller numbers where the common multiple is easily identifiable. The GCD method is efficient when you already know the GCD or need to calculate both the GCD and LCM simultaneously.
Applications of LCMs:
Understanding LCMs has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses that depart from the same station at different intervals. The LCM helps determine when the buses will depart simultaneously again.
-
Fraction Operations: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
-
Cyclic Processes: LCMs are used in problems involving repetitive events, such as the cycles of planets or machinery operations.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, simply include all prime factors from all the numbers, taking the highest power of each. For the GCD method, you would need to iteratively calculate the GCD of pairs of numbers and then use the formula to find the LCM.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The least common multiple (LCM) is the smallest number that is a multiple of all the given numbers. The greatest common divisor (GCD) is the largest number that divides all the given numbers without leaving a remainder.
-
Q: Can the LCM of two numbers be smaller than one of the numbers?
- A: No, the LCM of two numbers will always be greater than or equal to the larger of the two numbers.
-
Q: What if the two numbers are co-prime (their GCD is 1)?
- A: If the GCD of two numbers is 1, then their LCM is simply the product of the two numbers.
-
Q: How do I calculate the LCM of three or more numbers?
- A: You can extend the prime factorization method by considering all prime factors from all numbers, taking the highest power of each. Alternatively, you can calculate the LCM of two numbers first, and then find the LCM of the result and the third number, and so on.
-
Q: Are there online calculators to find the LCM?
- A: Yes, many online calculators are available that can calculate the LCM of any set of numbers. However, understanding the underlying principles and methods is far more valuable than simply using a calculator.
Conclusion:
Calculating the least common multiple is a fundamental concept in mathematics with numerous practical applications. Mastering different methods, like prime factorization and the GCD method, will not only help you solve problems efficiently but also deepen your understanding of number theory. While calculators can provide quick answers, grasping the underlying principles is crucial for applying this concept effectively in various mathematical and real-world contexts. Remember that practice is key to mastering LCM calculations and to appreciating the elegance and power of this mathematical concept. By understanding the different approaches, you’ll be well-equipped to tackle more complex problems involving LCMs and related concepts.
Latest Posts
Latest Posts
-
X Sqrt 1 X 2
Sep 20, 2025
-
What Is 1 5 Of 10
Sep 20, 2025
-
What Are Factors Of 76
Sep 20, 2025
-
What Times What Equals 42
Sep 20, 2025
-
Ml To Gallons Conversion Calculator
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 16 And 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.