1 3 4 X 3
saludintensiva
Sep 10, 2025 · 5 min read
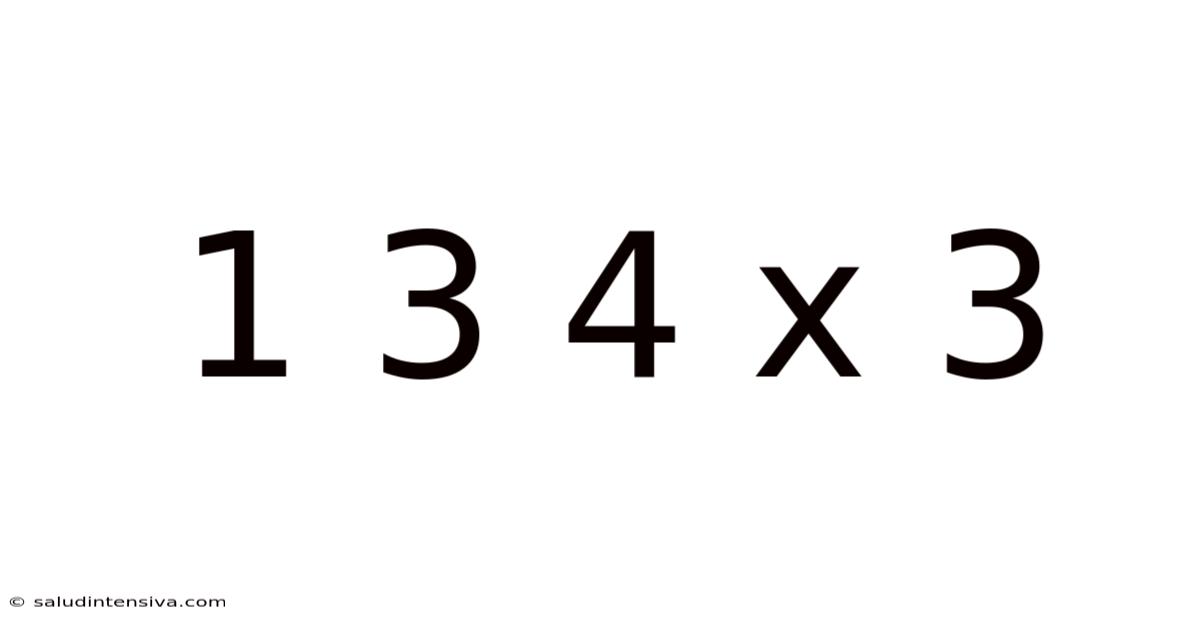
Table of Contents
Decoding 1 3 4 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical problem "1 3 4 x 3," delving far beyond the immediate answer to uncover the underlying principles of multiplication, its various applications, and its significance in broader mathematical concepts. We'll explore different approaches to solving this problem, discuss the properties of multiplication, and examine its role in diverse fields, from everyday calculations to advanced scientific modeling. This exploration will be accessible to a wide range of readers, from elementary school students to those seeking a refresher on fundamental mathematical concepts.
Understanding the Basics: What is Multiplication?
Multiplication is a fundamental arithmetic operation representing repeated addition. When we say "1 3 4 x 3," we're essentially asking: "What is the sum of three 134s?" This can be visualized as three groups of 134 objects each. The number 134 is the multiplicand, and the number 3 is the multiplier. The result, obtained by multiplying the multiplicand by the multiplier, is the product.
Different Ways to Solve 134 x 3:
There are several ways to approach this multiplication problem:
-
Repeated Addition: The most basic method is to add 134 three times: 134 + 134 + 134 = 402. This method directly reflects the definition of multiplication as repeated addition.
-
Standard Algorithm (Column Method): This is the most common method taught in schools. We arrange the numbers vertically and multiply each digit of the multiplicand (134) by the multiplier (3), carrying over any tens or hundreds to the next column.
134
x 3
-----
402
- Distributive Property: The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this to break down 134 into 100 + 30 + 4, and then multiply each part by 3:
(100 + 30 + 4) x 3 = (100 x 3) + (30 x 3) + (4 x 3) = 300 + 90 + 12 = 402
- Lattice Multiplication: This visually appealing method involves creating a grid and performing individual multiplications within the grid before summing the results diagonally. While less commonly used, it can be a helpful alternative for understanding the process.
Exploring Properties of Multiplication:
Understanding the properties of multiplication allows us to solve problems more efficiently and to develop a deeper understanding of the operation itself. Key properties include:
-
Commutative Property: The order of the numbers doesn't affect the product. 134 x 3 = 3 x 134 = 402.
-
Associative Property: When multiplying more than two numbers, the grouping doesn't matter. (a x b) x c = a x (b x c).
-
Identity Property: Multiplying any number by 1 results in the same number. 134 x 1 = 134.
-
Zero Property: Multiplying any number by 0 results in 0. 134 x 0 = 0.
-
Distributive Property (as explained above): This property allows us to break down complex multiplications into simpler ones.
Applications of Multiplication:
Multiplication is far more than just a schoolroom exercise; it’s a fundamental tool applied across countless fields:
-
Everyday Life: Calculating the total cost of multiple items, determining the area of a room, converting units of measurement, sharing items equally, and many more everyday situations rely heavily on multiplication. For example, if you buy 3 apples at $1.34 each, the total cost is 134 x 3 = $4.02.
-
Engineering and Physics: Multiplication is crucial in calculations involving forces, velocities, and acceleration. Designers and engineers use multiplication to scale blueprints, calculate material requirements, and simulate physical phenomena.
-
Finance and Business: Calculating profits, losses, interest rates, taxes, and investment returns all involve multiplication. Understanding compound interest, for example, requires a solid grasp of multiplication and exponential growth.
-
Computer Science: Multiplication is at the heart of computer algorithms and data processing. Matrix multiplication, a more complex form of multiplication, is fundamental to computer graphics, machine learning, and scientific computing.
-
Chemistry and Biology: Stoichiometry, the study of the quantitative relationships between reactants and products in chemical reactions, relies extensively on multiplication. Similarly, population growth models in biology often involve multiplicative factors.
Multiplication in Advanced Mathematics:
The simple act of multiplying 134 by 3 opens doors to a vast world of more complex mathematical concepts:
-
Algebra: Multiplication is a core component of algebraic expressions and equations. Solving for unknown variables often requires manipulating multiplicative relationships.
-
Calculus: Derivatives and integrals, fundamental concepts in calculus, involve multiplication and its inverse, division. Understanding the rate of change and accumulation requires a thorough understanding of multiplication.
-
Linear Algebra: Matrix multiplication, as mentioned earlier, is a cornerstone of linear algebra, a branch of mathematics with wide-ranging applications in computer science, physics, and engineering.
Frequently Asked Questions (FAQ):
-
What if I made a mistake in my multiplication? Carefully check your work using a different method, such as repeated addition or the distributive property. If you're still unsure, ask a teacher or tutor for help.
-
Are there other ways to visualize multiplication? Yes! Using manipulatives like counters or blocks can provide a concrete representation of the operation, particularly helpful for younger learners. Area models, where the numbers are represented as dimensions of a rectangle, are another useful visualization technique.
-
How can I improve my multiplication skills? Practice is key! Work through various problems, use different methods, and seek out resources like worksheets, online games, and educational apps to reinforce your understanding.
-
Why is multiplication important? Multiplication is a fundamental building block for many other mathematical concepts and is essential for solving problems in numerous fields. A strong understanding of multiplication is crucial for academic success and everyday life.
Conclusion: Beyond 134 x 3
The seemingly straightforward problem of "1 3 4 x 3" serves as a gateway to a much broader understanding of mathematics. From its basic definition as repeated addition to its sophisticated applications in advanced fields, multiplication underpins a significant portion of our mathematical knowledge and its practical application in the world. By exploring the different methods of solving this problem and understanding its underlying properties and applications, we gain a deeper appreciation for the power and versatility of this fundamental arithmetic operation. Mastering multiplication is not just about getting the right answer; it's about cultivating a deeper understanding of numbers, patterns, and the interconnectedness of mathematical concepts. The journey from a simple calculation to a comprehensive understanding of its implications highlights the beauty and practicality of mathematics in our daily lives and beyond.
Latest Posts
Latest Posts
-
150 Percent As A Decimal
Sep 10, 2025
-
Flipping A Coin 1000 Times
Sep 10, 2025
-
How To Multiply Divide Fractions
Sep 10, 2025
-
20 Percent As A Decimal
Sep 10, 2025
-
Estimating Sums And Differences Fractions
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 3 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.