20 Percent As A Decimal
saludintensiva
Sep 10, 2025 · 6 min read
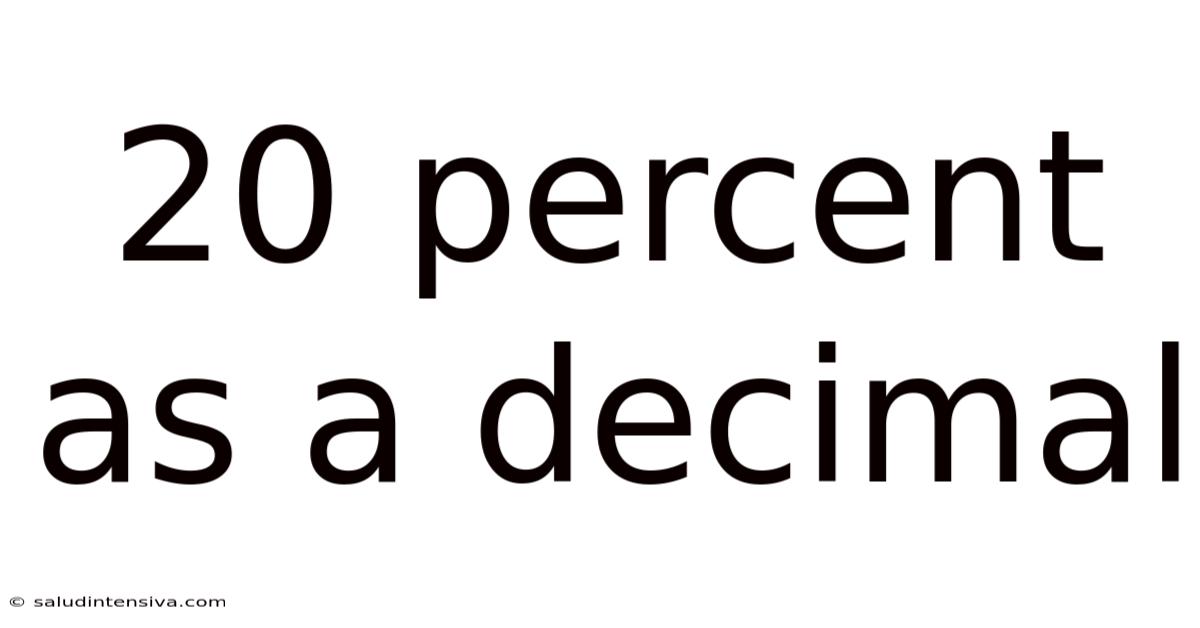
Table of Contents
Understanding 20 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and has wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial statements and statistical data. This comprehensive guide delves into the concept of 20 percent as a decimal, explaining the conversion process, its practical applications, and addressing frequently asked questions. We'll explore the underlying principles to ensure a thorough grasp of this crucial mathematical concept.
What is a Percentage?
Before diving into the specifics of 20 percent as a decimal, let's establish a clear understanding of what a percentage is. A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). Therefore, 20 percent means 20 out of 100, or 20/100.
Converting Percentages to Decimals: The Fundamental Process
The conversion of a percentage to a decimal involves a straightforward process. To convert any percentage to its decimal equivalent, simply divide the percentage by 100. This is because a percentage is a fraction with a denominator of 100. Dividing by 100 is equivalent to moving the decimal point two places to the left.
Let's illustrate this with the example of 20 percent:
- 20% / 100 = 0.20
Therefore, 20 percent as a decimal is 0.20, or simply 0.2. The trailing zero in 0.20 is often omitted, as it doesn't change the numerical value.
Why is Understanding this Conversion Important?
The ability to convert percentages to decimals is crucial for several reasons:
-
Mathematical Calculations: Many mathematical operations, particularly those involving multiplication and division, are significantly easier to perform using decimals rather than percentages. For instance, calculating 20% of a number is much simpler when you use the decimal equivalent (0.2) instead of the percentage.
-
Financial Applications: Percentages are ubiquitous in finance. Understanding the decimal equivalent allows for easier calculation of interest rates, discounts, taxes, and profit margins. For example, calculating the interest earned on a savings account or the discount on a sale item is simplified using decimals.
-
Data Analysis and Statistics: In data analysis and statistics, percentages are often converted to decimals for use in various calculations and statistical tests. This allows for smoother integration into statistical software and simplifies interpretations of results.
-
Scientific Applications: Many scientific fields utilize percentages, often converted to decimals, in their data representation and calculations. This ensures consistent data handling and facilitates accurate scientific analysis.
Practical Applications of 20 Percent as a Decimal (0.2)
Let's explore some real-world scenarios where understanding 20% as 0.2 is beneficial:
-
Calculating Sales Discounts: A store offers a 20% discount on all items. To calculate the discount on an item priced at $50, you would multiply the price by 0.2: $50 * 0.2 = $10. The discount is $10, and the final price is $40.
-
Determining Sales Tax: If the sales tax in a region is 20%, the tax on a $100 purchase can be calculated as: $100 * 0.2 = $20.
-
Calculating Interest Earned: If a savings account offers an annual interest rate of 20%, and you deposit $1000, the interest earned after one year would be: $1000 * 0.2 = $200.
-
Analyzing Statistical Data: Imagine a survey shows that 20% of respondents prefer a particular product. The decimal equivalent, 0.2, is often used in statistical analysis to calculate confidence intervals and other statistical measures.
-
Portioning Ingredients: In cooking, a recipe might call for 20% of a certain ingredient. Converting 20% to 0.2 simplifies the calculation to determine the correct amount.
Beyond the Basics: Working with More Complex Percentages
While we've focused on 20 percent, the principles of converting percentages to decimals remain the same for any percentage. For example:
- 50% = 0.50 or 0.5
- 75% = 0.75
- 15% = 0.15
- 2.5% = 0.025 (Note the extra zero before the 2)
Remember to always divide the percentage by 100 or move the decimal point two places to the left. For percentages less than 1%, you'll need to add a leading zero before the decimal point.
Explaining the Conversion Scientifically
From a scientific perspective, the conversion from percentage to decimal is based on the fundamental concept of representing a part of a whole. The percentage represents the part, and the whole is always considered 100 units. Converting to a decimal expresses this part as a fraction of 1 (the whole).
The mathematical operation of dividing by 100 is essentially scaling down the percentage to a representation where the whole is 1. This decimal representation is more convenient for algebraic manipulations and various calculations in various scientific disciplines.
Frequently Asked Questions (FAQs)
Q: Can I convert a decimal back to a percentage?
A: Yes, absolutely! To convert a decimal back to a percentage, simply multiply the decimal by 100 and add the percent sign (%). For example, 0.2 * 100 = 20%, 0.75 * 100 = 75%.
Q: What if the percentage is a decimal itself, like 20.5%?
A: Follow the same process: divide by 100. 20.5% / 100 = 0.205.
Q: Is there a shortcut for converting percentages to decimals?
A: Yes, as mentioned earlier, you can simply move the decimal point two places to the left. If there's no visible decimal point (as in 20%), it's understood to be at the end of the number.
Q: Why is using decimals often preferred over percentages in calculations?
A: Decimals are generally preferred for mathematical calculations because they directly represent a fraction of one, which simplifies arithmetic operations like multiplication, division, and integration within more complex equations. Percentages, while intuitively understandable, require an extra step of conversion before being used in most calculations.
Q: Are there any instances where using percentages is better than decimals?
A: While decimals are usually preferred for calculations, percentages are often better for representing proportions in a way that is more easily understood by a general audience. They provide a more intuitive way to communicate relative proportions or changes.
Conclusion
Understanding how to convert 20 percent to its decimal equivalent, 0.2, is a crucial skill with wide-ranging applications in various fields. This conversion, based on the fundamental principle of representing a part of a whole, streamlines numerous mathematical operations, from calculating discounts and taxes to analyzing statistical data. Mastering this concept empowers you to confidently navigate various numerical scenarios in everyday life and across diverse academic and professional pursuits. By grasping the principles outlined in this guide, you'll be well-equipped to handle percentage-to-decimal conversions with ease and accuracy. Remember the simple process: divide by 100 (or move the decimal point two places to the left), and you'll have a strong foundation for tackling a wide array of numerical challenges involving percentages.
Latest Posts
Latest Posts
-
5 To The 4th Power
Sep 10, 2025
-
1 15 Random Number Generator
Sep 10, 2025
-
Lcm For 8 And 3
Sep 10, 2025
-
3 5 As A Mixed Number
Sep 10, 2025
-
What Is Equivalent To 10 12
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.