1 3/5 As A Percent
saludintensiva
Sep 19, 2025 · 5 min read
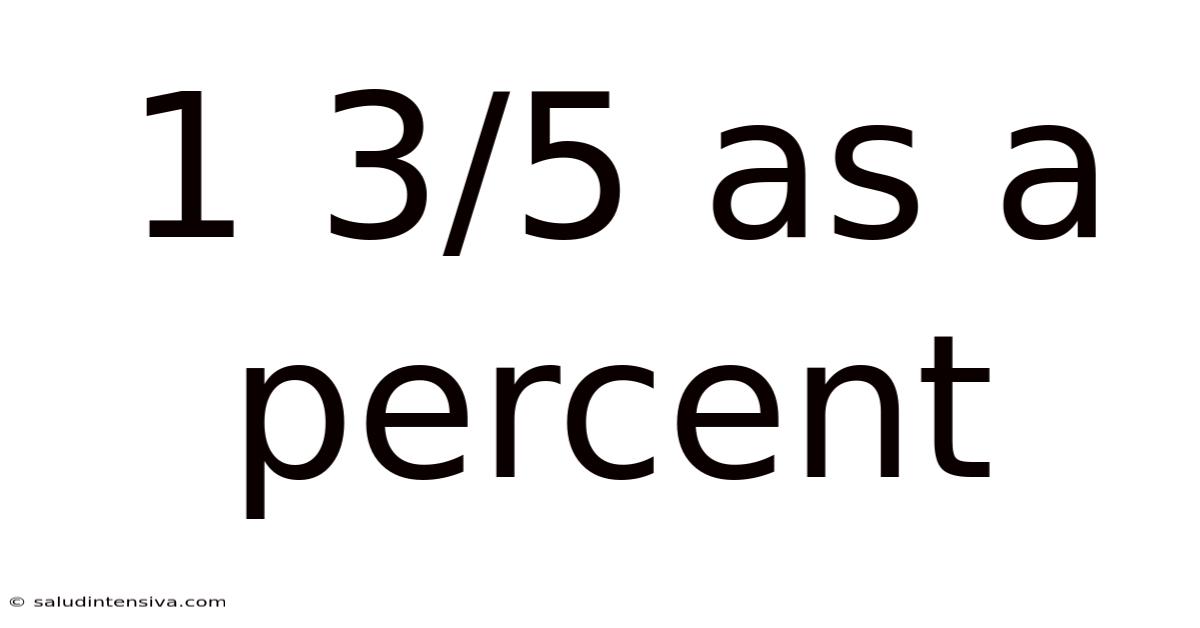
Table of Contents
1 3/5 as a Percent: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will walk you through the process of converting the mixed number 1 3/5 into a percentage, explaining the underlying concepts and providing examples to solidify your understanding. We will also explore related concepts and answer frequently asked questions.
Understanding Fractions, Decimals, and Percentages
Before diving into the conversion, let's refresh our understanding of these three interconnected concepts:
-
Fractions: Represent parts of a whole. They consist of a numerator (top number) and a denominator (bottom number). For example, in the fraction 3/5, 3 is the numerator and 5 is the denominator. This signifies three out of five equal parts.
-
Decimals: Represent fractions using a base-ten system. The decimal point separates the whole number part from the fractional part. For example, 0.6 represents six-tenths, equivalent to 6/10.
-
Percentages: Represent fractions or decimals as parts of a hundred. The symbol "%" indicates "per hundred". For instance, 60% means 60 out of 100, equivalent to 60/100 or 0.6.
These three concepts are interchangeable, and understanding their relationships is key to performing conversions.
Converting 1 3/5 to a Percentage: A Step-by-Step Guide
To convert 1 3/5 to a percentage, we'll follow a series of straightforward steps:
Step 1: Convert the Mixed Number to an Improper Fraction
A mixed number combines a whole number and a fraction (e.g., 1 3/5). To convert it to an improper fraction (where the numerator is larger than the denominator), we multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same.
1 3/5 = (1 * 5 + 3) / 5 = 8/5
Step 2: Convert the Improper Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator.
8/5 = 1.6
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol.
1.6 * 100 = 160%
Therefore, 1 3/5 is equivalent to 160%.
Alternative Method: Direct Conversion
While the above method is systematic and easy to understand, you can also approach this conversion more directly. Remember that a percentage is a fraction with a denominator of 100. We can manipulate the fraction 8/5 to achieve this:
-
Find an equivalent fraction with a denominator of 100: To do this, we need to find a number that, when multiplied by 5, equals 100. That number is 20.
-
Multiply both the numerator and the denominator by 20:
(8 * 20) / (5 * 20) = 160/100
-
Express the fraction as a percentage: Since the denominator is 100, the numerator directly represents the percentage. Therefore, 160/100 = 160%.
This method highlights the fundamental concept of percentages as fractions out of 100.
Understanding the Significance of 160%
It's crucial to understand what 160% signifies. A percentage greater than 100% indicates a value exceeding the original whole. In this context, 160% means that the quantity represented by 1 3/5 is 1.6 times the original whole or 60% more than the original whole. This is a common occurrence in various scenarios, such as calculating percentage increases, growth rates, or comparing values.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is essential in numerous real-world situations:
-
Financial Calculations: Calculating interest rates, discounts, profit margins, and tax rates all require a firm grasp of percentage conversions. For example, a 160% increase in profits signifies a significantly positive financial outcome.
-
Data Analysis: Representing data in percentage form often simplifies interpretation and comparison. Imagine analyzing survey results: converting the fraction of respondents choosing a particular option into a percentage makes the data easier to visualize and understand.
-
Scientific Calculations: Many scientific calculations involve expressing results as percentages, such as calculating the percentage error in an experiment or expressing the concentration of a solution.
-
Everyday Life: Understanding percentages is helpful for calculating tips in restaurants, figuring out sales discounts, or understanding the nutritional information on food labels.
Frequently Asked Questions (FAQ)
Q1: Can I convert a percentage back to a fraction or decimal?
Yes, absolutely! To convert a percentage to a decimal, divide by 100. To convert a decimal to a fraction, write the decimal as a fraction over 1, and then simplify the fraction by finding the greatest common factor between the numerator and denominator. For example, 160% as a decimal is 1.6 (160/100), and 1.6 as a fraction is 8/5.
Q2: What if I have a complex fraction?
Complex fractions involve fractions within fractions. To convert them to a percentage, simplify the complex fraction first by performing the necessary operations of multiplication and division. Once you have a simple fraction, you can follow the steps outlined earlier to convert it to a percentage.
Q3: How do I calculate percentage increase or decrease?
Percentage increase or decrease is calculated using the formula: [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase, while a negative result indicates a decrease. Understanding the conversion of fractions and decimals to percentages is critical for interpreting these results.
Q4: Are there any online tools or calculators to assist with percentage conversions?
Yes, numerous online calculators are available that can perform percentage conversions automatically. These can be a helpful tool for double-checking your work or for quickly converting complex fractions. However, understanding the underlying principles remains crucial for building a strong mathematical foundation.
Conclusion
Converting 1 3/5 to a percentage, resulting in 160%, is a straightforward process involving several steps: converting the mixed number to an improper fraction, then to a decimal, and finally to a percentage. Understanding this conversion, along with the underlying concepts of fractions, decimals, and percentages, is essential for tackling a wide range of mathematical problems and real-world applications. The ability to confidently perform these conversions is a valuable skill that will serve you well in various academic, professional, and personal contexts. Mastering this skill empowers you to analyze data, interpret financial information, and make informed decisions in various facets of your life.
Latest Posts
Latest Posts
-
13000 Square Feet In Acres
Sep 19, 2025
-
34 Percent As A Decimal
Sep 19, 2025
-
15 35 Is What Time
Sep 19, 2025
-
How Long Is 56 Minutes
Sep 19, 2025
-
21 Percent As A Decimal
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 3/5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.