1.3 As A Mixed Number
saludintensiva
Sep 16, 2025 · 6 min read
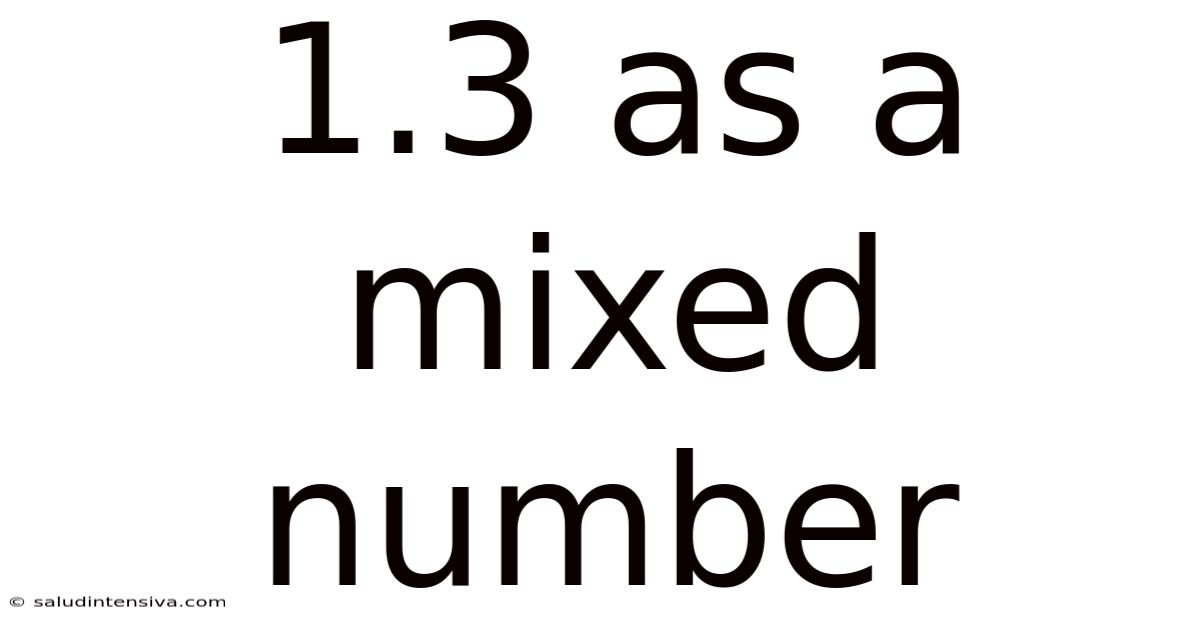
Table of Contents
Understanding 1.3 as a Mixed Number: A Comprehensive Guide
The decimal 1.3 might seem simple at first glance, but understanding its representation as a mixed number opens doors to a deeper understanding of fractions and their relationship to decimals. This article provides a comprehensive guide to converting 1.3 into a mixed number, exploring the underlying mathematical principles, and addressing common questions and misconceptions. We will delve into the practical applications and demonstrate how this seemingly basic conversion can be a foundational step in more advanced mathematical concepts.
Introduction: Decimals and Mixed Numbers
Before diving into the conversion, let's clarify the terms. A decimal is a way of expressing a number using a base-ten system, where the digits to the right of the decimal point represent fractions with denominators of powers of 10 (tenths, hundredths, thousandths, etc.). A mixed number, on the other hand, is a combination of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). Converting between decimals and mixed numbers is a crucial skill in mathematics, bridging the gap between these two common number representations.
Converting 1.3 to a Mixed Number: A Step-by-Step Approach
The conversion of 1.3 to a mixed number involves recognizing the whole number part and the fractional part.
-
Identify the Whole Number: The digit to the left of the decimal point represents the whole number. In 1.3, the whole number is 1.
-
Identify the Fractional Part: The digits to the right of the decimal point represent the fractional part. In 1.3, the fractional part is 0.3.
-
Convert the Decimal Fraction to a Common Fraction: To express 0.3 as a fraction, we recognize that it represents three-tenths. Therefore, 0.3 can be written as 3/10.
-
Combine the Whole Number and the Fraction: Now we combine the whole number (1) and the fraction (3/10) to form the mixed number. The result is 1 3/10.
Therefore, 1.3 expressed as a mixed number is 1 3/10.
Understanding the Mathematical Principles
The conversion process relies on the fundamental understanding of place value in the decimal system and the relationship between decimals and fractions. The decimal point acts as a separator between the whole number and the fractional part. Each digit to the right of the decimal point represents a progressively smaller fraction of a whole.
-
Place Value: In the decimal 1.3, the digit '1' is in the ones place, representing one whole unit. The digit '3' is in the tenths place, representing three-tenths of a unit (3/10).
-
Fraction Representation: Every decimal can be expressed as a fraction. The number of digits to the right of the decimal point determines the denominator of the fraction. For example, 0.3 has one digit after the decimal, making the denominator 10. 0.03 would have a denominator of 100, and so on. The numerator is simply the digits to the right of the decimal point, without the decimal point.
Further Exploration: Equivalent Fractions and Simplification
While 1 3/10 is a perfectly valid mixed number representation of 1.3, it's always worth considering whether the fraction part can be simplified. In this case, 3 and 10 share no common factors other than 1, meaning the fraction is already in its simplest form. However, if we had a decimal like 1.25 (which is equivalent to 1 1/4), we could simplify the fraction to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Practical Applications of Mixed Numbers
Understanding the conversion between decimals and mixed numbers is essential in various contexts:
-
Measurement: Many real-world measurements use mixed numbers, such as 1 3/4 cups of flour or 2 1/2 inches of fabric. Converting decimals to mixed numbers facilitates easier understanding and practical application in these situations.
-
Cooking and Baking: Recipes often use fractions and mixed numbers for ingredient quantities. Being able to convert between decimals and mixed numbers ensures accurate measurements and successful cooking or baking.
-
Construction and Engineering: Precision in construction and engineering requires accurate measurements. Converting decimals to mixed numbers provides a clearer visual representation of the precise measurements needed.
-
Finance: Calculations involving money often require converting between decimals and mixed numbers for clarity and ease of understanding.
-
Data Analysis: In data analysis, understanding both decimal and mixed number representations can be useful for interpreting data and making sense of various measurements or quantities.
Frequently Asked Questions (FAQ)
Q: Can all decimals be expressed as mixed numbers?
A: No. Only decimals that are greater than or equal to 1 can be expressed as mixed numbers. Decimals less than 1 are represented as proper fractions.
Q: What if the decimal has more than one digit after the decimal point?
A: If the decimal has more than one digit after the decimal point (e.g., 1.25), follow the same steps: Identify the whole number, convert the decimal fraction to a common fraction (in this case, 25/100), and then combine the whole number and the fraction to form the mixed number (1 25/100, which simplifies to 1 1/4). The denominator will be a power of 10 (10, 100, 1000, etc.), depending on the number of digits after the decimal point.
Q: Why is it important to learn this conversion?
A: Understanding the conversion between decimals and mixed numbers helps build a strong foundation in fractions and decimals, which are fundamental concepts in mathematics used across various fields. It improves mathematical fluency and problem-solving skills.
Q: Are there any online tools or calculators that can help with this conversion?
A: While many online calculators can perform decimal-to-fraction conversions, understanding the underlying mathematical process is crucial for true mastery. Using a calculator should be a supplementary tool, not a replacement for learning the conversion method.
Conclusion: Mastering the Conversion
Converting 1.3 to the mixed number 1 3/10 might seem like a small step, but it embodies a significant understanding of fundamental mathematical principles. This conversion showcases the interconnectedness of decimals and fractions, highlighting the flexibility and power of different numerical representations. Mastering this conversion lays the groundwork for tackling more complex mathematical challenges involving fractions and decimals. By understanding the underlying process and practicing regularly, you'll build a solid foundation for success in mathematics and related fields. Remember, the key is to practice regularly and apply this knowledge in various contexts to solidify your understanding. The seemingly simple act of converting 1.3 to 1 3/10 opens a world of possibilities in mathematical understanding and application.
Latest Posts
Latest Posts
-
26 Acres To Sq Ft
Sep 16, 2025
-
4 5 X 1 6
Sep 16, 2025
-
Absolute Value Of 4 2
Sep 16, 2025
-
5 2 As A Percentage
Sep 16, 2025
-
Gcf Of 14 And 56
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1.3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.