1 3 Of 2 3
saludintensiva
Sep 15, 2025 · 5 min read
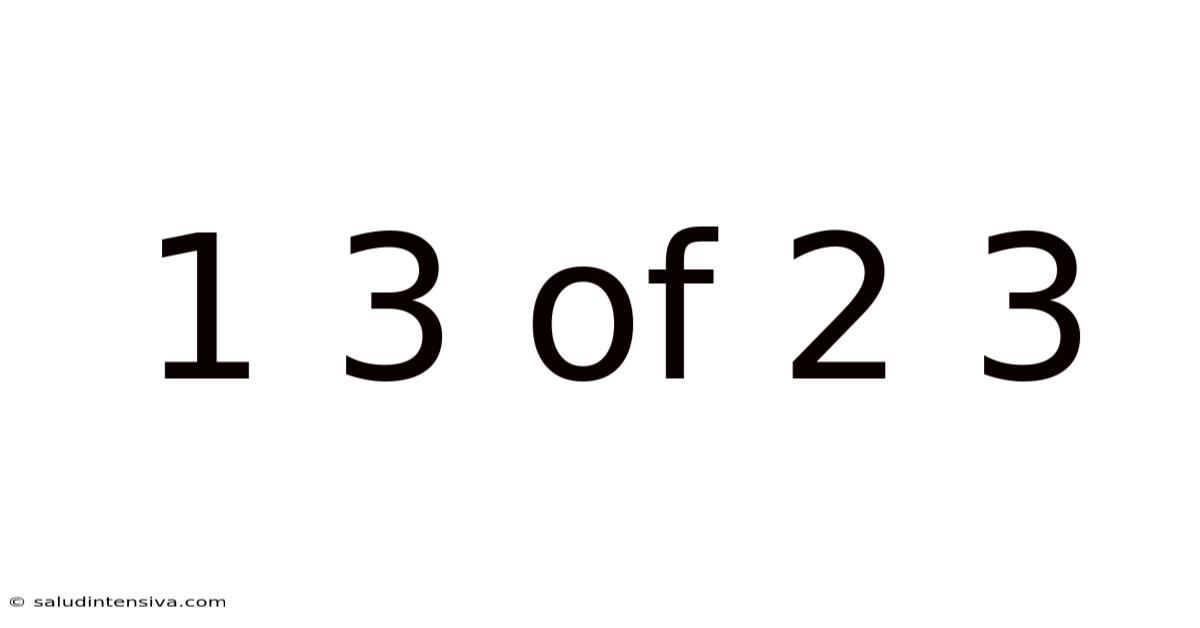
Table of Contents
Decoding the Enigma: Understanding 1/3 of 2/3
The seemingly simple fraction "1/3 of 2/3" often trips up students and even adults. It's a fundamental concept in mathematics, touching upon the core principles of fractions, multiplication, and simplification. This article will delve deep into understanding this calculation, explaining the process step-by-step, providing the scientific reasoning behind it, and addressing frequently asked questions. By the end, you'll not only know the answer but also possess a stronger grasp of fractional arithmetic. This comprehensive guide aims to break down the concept into easily digestible parts, making it accessible to learners of all backgrounds.
Understanding the Fundamentals: Fractions and Multiplication
Before tackling "1/3 of 2/3," let's refresh our understanding of fractions and how they interact with multiplication. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, 1/3 represents one part out of three equal parts. Similarly, 2/3 represents two parts out of three equal parts.
When we multiply fractions, we multiply the numerators together and the denominators together. This is a fundamental rule that governs fractional arithmetic. Let's illustrate:
- (a/b) * (c/d) = (ac) / (bd)
Calculating 1/3 of 2/3: A Step-by-Step Guide
Now, let's apply this knowledge to solve "1/3 of 2/3." The word "of" in mathematics signifies multiplication. Therefore, the expression can be rewritten as:
(1/3) * (2/3)
Following the rule of multiplying fractions:
- Multiply the numerators: 1 * 2 = 2
- Multiply the denominators: 3 * 3 = 9
This gives us the result: 2/9
Therefore, 1/3 of 2/3 is 2/9.
Visualizing the Solution: A Geometric Approach
Understanding fractions can be significantly enhanced through visual representation. Imagine a square representing the whole.
-
Divide the square into three equal vertical strips. Each strip represents 1/3.
-
Shade two of these strips to represent 2/3.
-
Now, divide the entire square into three equal horizontal strips. This further subdivides the square into a 3x3 grid.
-
Focus on the area representing 1/3 of the 2/3 that was already shaded. You'll observe that this encompasses 2 out of the 9 smaller squares. This visually confirms that 1/3 of 2/3 equals 2/9.
The Scientific Rationale: Mathematical Justification
The process we followed is grounded in the principles of fractional arithmetic and the distributive property of multiplication over addition. We can also approach the problem using the concept of repeated addition:
Imagine we have 2/3 of something. To find 1/3 of that 2/3, we can divide 2/3 into three equal parts and take one part. Dividing a fraction by a number is equivalent to multiplying it by the reciprocal of that number. So, we can express it as:
(2/3) / 3 = (2/3) * (1/3) = 2/9
This demonstrates that our earlier calculation using direct multiplication arrives at the same correct answer.
Simplifying Fractions: Reducing to the Lowest Terms
In many cases, the resulting fraction can be simplified by reducing it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In the case of 2/9, the GCD of 2 and 9 is 1. Since dividing by 1 doesn't change the fraction's value, 2/9 is already in its simplest form.
Frequently Asked Questions (FAQ)
Here are some common questions related to understanding 1/3 of 2/3:
Q1: Can I solve this problem using decimals instead of fractions?
A1: Yes, you can convert the fractions to decimals before performing the calculation. 1/3 ≈ 0.333... and 2/3 ≈ 0.666... Multiplying these gives approximately 0.222..., which is approximately equal to 2/9. However, using decimals can introduce rounding errors, particularly with repeating decimals like 1/3 and 2/3, making the fractional method more precise.
Q2: What if the question was "2/3 of 1/3"? Would the answer be the same?
A2: No, the order of multiplication matters. While 2/3 * 1/3 also equals 2/9, it represents a different scenario. It asks for two-thirds of one-third, a conceptually distinct situation from taking one-third of two-thirds. The numerical result is identical, but the visual representation would be different.
Q3: Are there any real-world applications for this type of calculation?
A3: Yes! Fractional arithmetic is essential in numerous real-world situations, such as:
- Baking: Adjusting recipes that require fractional quantities of ingredients.
- Construction: Calculating the amount of materials needed for a project based on fractional measurements.
- Finance: Determining fractional ownership in a business or investment.
- Science: Numerous scientific calculations and measurements involve fractions and proportional reasoning.
Q4: How can I improve my understanding of fractions?
A4: Consistent practice is key. Work through various fraction problems, focusing on understanding the underlying concepts rather than just memorizing formulas. Visual aids, such as diagrams and manipulatives, can also help solidify your understanding. Try working through different types of fraction problems, including addition, subtraction, multiplication, and division.
Conclusion: Mastering Fractional Arithmetic
Understanding "1/3 of 2/3" is not just about getting the answer (2/9); it's about grasping the fundamental principles of fractional arithmetic. This article has explored this concept from various perspectives, providing step-by-step calculations, visual representations, and a detailed mathematical justification. By understanding the underlying principles and practicing regularly, you can confidently tackle similar problems and strengthen your foundation in mathematics. Remember that consistent practice and a willingness to explore the underlying concepts are essential for mastering this and other essential mathematical skills. Don't hesitate to revisit the steps and visual examples to solidify your comprehension and continue building your mathematical confidence.
Latest Posts
Latest Posts
-
5 2 5 As A Decimal
Sep 15, 2025
-
3 1 10 As A Decimal
Sep 15, 2025
-
5 2 6 2 5 6
Sep 15, 2025
-
What Are Factors Of 19
Sep 15, 2025
-
First 6 Multiples Of 10
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.