5 2/5 As A Decimal
saludintensiva
Sep 15, 2025 · 5 min read
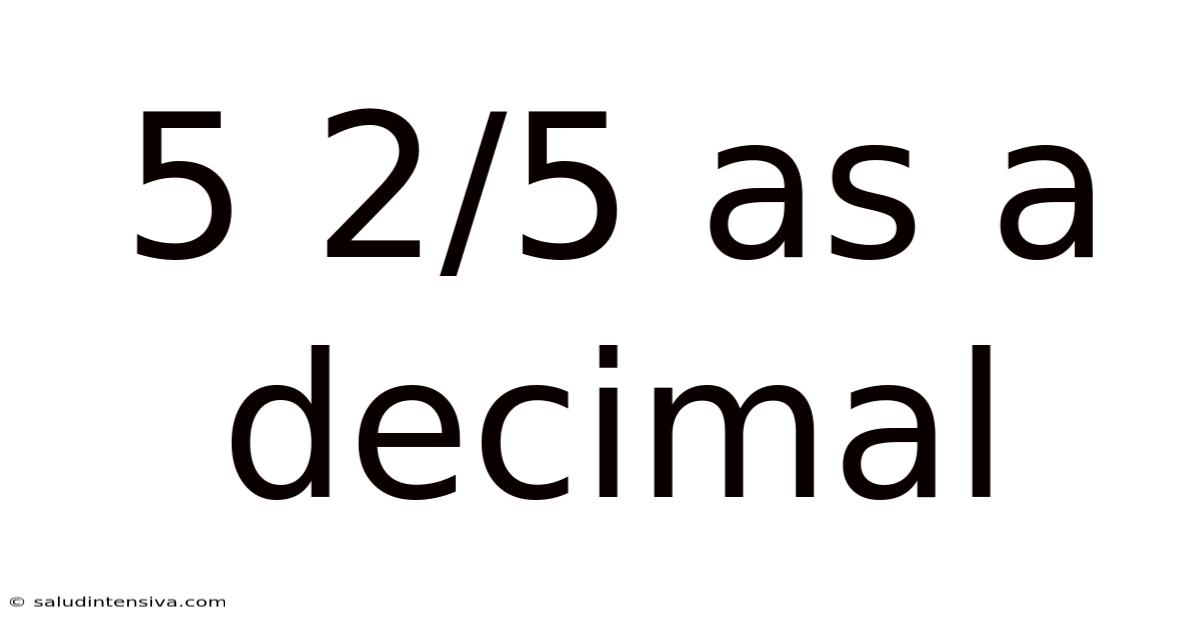
Table of Contents
5 2/5 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, essential for various applications from everyday calculations to complex scientific computations. This article will thoroughly explore how to convert the mixed number 5 2/5 into its decimal equivalent, providing a step-by-step guide suitable for all levels of understanding. We'll delve into the underlying principles, offer alternative approaches, and address frequently asked questions, ensuring a comprehensive understanding of this crucial concept.
Understanding Mixed Numbers and Decimals
Before we begin the conversion, let's clarify the terms involved. A mixed number combines a whole number and a fraction, like 5 2/5. A decimal is a way of expressing a number using a base-ten system, where digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.). Converting a mixed number to a decimal involves expressing the fractional part as a decimal and then adding it to the whole number part.
Step-by-Step Conversion of 5 2/5 to a Decimal
There are two primary methods to convert 5 2/5 into a decimal:
Method 1: Converting the Fraction to a Decimal Directly
This method involves focusing solely on the fractional part, 2/5, before combining it with the whole number.
-
Divide the numerator by the denominator: The fraction 2/5 represents 2 divided by 5. Perform this division: 2 ÷ 5 = 0.4
-
Add the whole number: Now, add the whole number part (5) to the decimal equivalent of the fraction (0.4): 5 + 0.4 = 5.4
Therefore, 5 2/5 as a decimal is 5.4.
Method 2: Converting the Mixed Number to an Improper Fraction First
This approach involves transforming the mixed number into an improper fraction before converting it to a decimal. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert to an improper fraction: To convert 5 2/5 to an improper fraction, multiply the whole number (5) by the denominator (5), add the numerator (2), and keep the same denominator (5): (5 x 5) + 2 = 27. The improper fraction becomes 27/5.
-
Divide the numerator by the denominator: Now, divide the numerator (27) by the denominator (5): 27 ÷ 5 = 5.4
Again, we arrive at the same result: 5 2/5 as a decimal is 5.4.
The Underlying Principle: Decimal Representation of Fractions
The fundamental principle behind converting fractions to decimals lies in understanding that a fraction represents a division. The fraction a/b is equivalent to a divided by b. When we perform this division, the result is a decimal representation of the fraction. This works for both proper fractions (numerator < denominator) and improper fractions (numerator ≥ denominator). In the case of 5 2/5, we are essentially dividing 2 by 5, which yields 0.4, representing two-fifths. Adding the whole number 5 gives us the final decimal of 5.4.
Alternative Methods and Considerations
While the above methods are the most straightforward, there are other approaches, particularly useful for more complex fractions:
-
Using a calculator: Modern calculators effortlessly handle fraction-to-decimal conversions. Simply input the fraction (2/5 or 27/5) and press the equals button. The calculator will directly display the decimal equivalent.
-
Long division: For those who prefer a manual approach and are comfortable with long division, this method allows for a step-by-step calculation of the division of the numerator by the denominator.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is invaluable in various contexts:
-
Financial calculations: Dealing with percentages, interest rates, and monetary amounts frequently requires converting fractions to decimals for accurate calculations.
-
Measurement and engineering: Precision in measurements necessitates decimal representations for accuracy in calculations and designs.
-
Scientific computations: Many scientific formulas and calculations require decimal inputs for precise results.
-
Data analysis: Converting fractions to decimals simplifies data analysis and allows for easier comparisons and interpretations.
-
Everyday life: From calculating tips at restaurants to measuring ingredients for baking, decimal understanding is frequently utilized in everyday situations.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be expressed as terminating decimals?
A1: No. Fractions with denominators that have prime factors other than 2 and 5 will result in non-terminating, repeating decimals. For example, 1/3 results in 0.333... (a repeating decimal).
Q2: What is the difference between a terminating and repeating decimal?
A2: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.25). A repeating decimal has a pattern of digits that repeats infinitely (e.g., 0.333...).
Q3: How do I convert a decimal back to a fraction?
A3: To convert a decimal back to a fraction, consider the place value of the last digit. For example, 0.4 is four-tenths, or 4/10. Simplify the fraction if possible. For repeating decimals, a more complex method is required.
Q4: What if the fraction is negative?
A4: If the fraction is negative (e.g., -5 2/5), perform the conversion as described above, and then add the negative sign to the final result. In this case, -5 2/5 = -5.4.
Conclusion
Converting the mixed number 5 2/5 to its decimal equivalent, 5.4, is a straightforward process achieved through dividing the numerator of the fractional part by the denominator and adding the result to the whole number. Understanding this fundamental conversion is crucial for various mathematical applications. This article has provided a comprehensive guide, covering different methods, clarifying underlying principles, and addressing frequently asked questions. Mastering this skill will enhance your mathematical abilities and prove invaluable across various fields of study and everyday life. By practicing these methods and exploring further related topics, you can build a solid foundation in fraction and decimal conversions. Remember, consistent practice is key to developing proficiency in mathematical concepts.
Latest Posts
Latest Posts
-
Is 1 2 Bigger Than 3 5
Sep 15, 2025
-
What Is 5 10 Simplified
Sep 15, 2025
-
3 5 5 As A Percent
Sep 15, 2025
-
19 3 As A Decimal
Sep 15, 2025
-
Present Value Of 1 Table
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 2/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.