1 5 Divided By 4
saludintensiva
Sep 15, 2025 · 6 min read
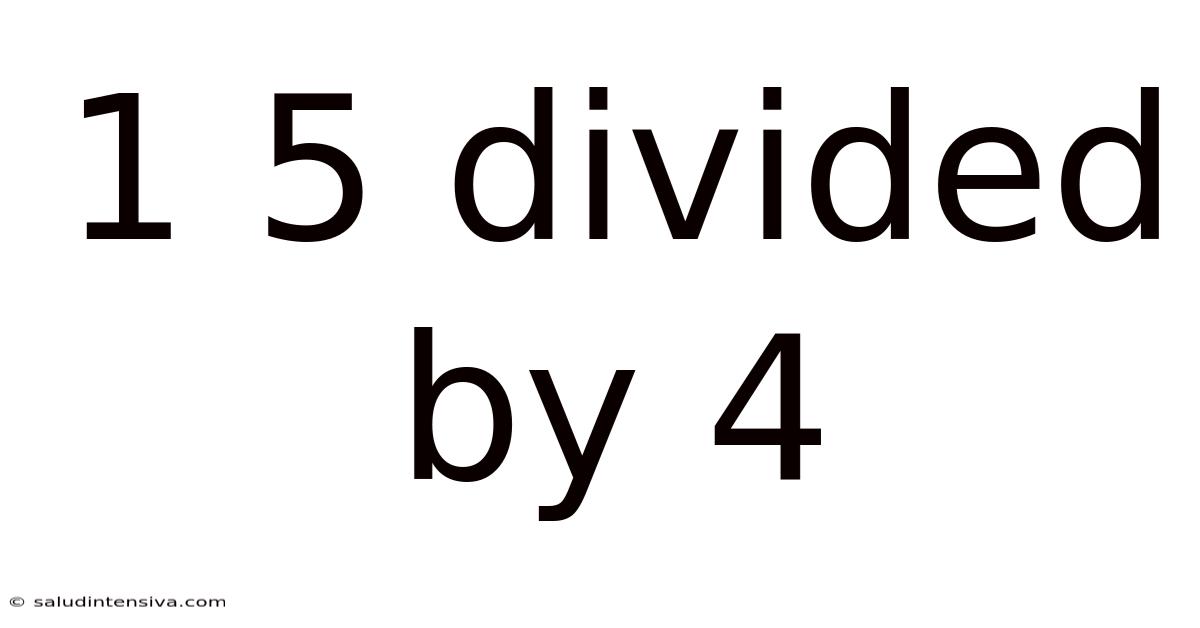
Table of Contents
Unveiling the Mystery: A Deep Dive into 15 Divided by 4
Many of us encounter division problems in our daily lives, from splitting bills with friends to calculating ingredient quantities for a recipe. Understanding division, especially with numbers that don't divide evenly, is crucial for navigating these everyday situations. This article delves into the seemingly simple problem of 15 divided by 4, exploring not just the answer but the underlying mathematical concepts and practical applications. We'll uncover the beauty of division, its various interpretations, and the valuable lessons it teaches us about numbers and problem-solving. This comprehensive guide is perfect for anyone looking to refresh their understanding of basic arithmetic or delve deeper into the fascinating world of mathematics.
Introduction: Understanding Division
Division, at its core, is the inverse operation of multiplication. While multiplication combines groups of equal size, division separates a quantity into equal parts. The problem 15 divided by 4 (often written as 15 ÷ 4 or 15/4) asks: "If we have 15 items, and we want to divide them equally among 4 groups, how many items will be in each group?"
The answer isn't a neat whole number; this is where the richness of division reveals itself. We'll explore the different ways to represent the solution, emphasizing the meaning behind each representation.
Calculating 15 Divided by 4: The Process
The traditional long division method offers a systematic way to solve 15 ÷ 4.
- Divide: How many times does 4 go into 15? It goes in 3 times (4 x 3 = 12).
- Multiply: Multiply the quotient (3) by the divisor (4): 3 x 4 = 12.
- Subtract: Subtract the product (12) from the dividend (15): 15 - 12 = 3.
- Bring Down: There are no more digits to bring down. The 3 is our remainder.
Therefore, 15 divided by 4 is 3 with a remainder of 3. We can represent this as:
- Mixed Number: 3 ¾ (three and three-quarters)
- Decimal: 3.75 (three point seventy-five)
- Improper Fraction: 15/4 (fifteen fourths)
Interpreting the Results: Different Perspectives
Each representation of the answer provides a slightly different perspective on the division problem:
-
Mixed Number (3 ¾): This format is intuitive and easy to visualize. We have 3 complete groups of 4 items each, and a remaining 3 items which can't form a full group.
-
Decimal (3.75): The decimal representation offers precision. Each group contains 3.75 items, showing the fractional part more explicitly. This representation is particularly useful in contexts where fractional quantities are meaningful, such as measuring liquids or weights.
-
Improper Fraction (15/4): This format emphasizes the total number of items divided into the number of groups. It's a concise mathematical representation and a foundation for more advanced algebraic manipulations.
The Remainder: Understanding its Significance
The remainder (3 in this case) is a crucial part of the solution. It indicates the number of items left over after dividing equally. The significance of the remainder depends on the context:
- Sharing items: If you're sharing 15 candies among 4 friends, each friend gets 3 candies, and you have 3 candies left.
- Measurement: If you're cutting a 15-meter rope into 4-meter lengths, you'll get 3 pieces of 4 meters each, with a 3-meter piece remaining.
- Division with Decimals: Converting the remainder into a decimal fraction provides a more precise result, useful in scientific or engineering calculations.
Understanding the remainder helps avoid misinterpretations and provides a complete picture of the division process.
Real-World Applications: Beyond the Classroom
The seemingly simple problem of 15 ÷ 4 finds its way into numerous real-world situations:
-
Baking: A recipe calls for 15 ounces of flour, and you want to divide it equally among 4 cakes. Each cake needs 3.75 ounces of flour.
-
Finance: Splitting a $15 bill evenly among 4 people results in each person paying $3.75.
-
Construction: Dividing a 15-foot beam into 4 equal sections leads to sections measuring 3.75 feet each.
-
Resource Allocation: Distributing 15 resources equally among 4 projects results in each project receiving 3 full resources, with 3 resources left to be allocated differently.
These examples highlight the practical relevance of mastering division and understanding the different forms of expressing the answer (mixed number, decimal, improper fraction).
Beyond the Basics: Extending the Concept
The problem 15 ÷ 4 serves as a stepping stone to understanding more complex division problems:
-
Dividing larger numbers: The same long division method applies to larger numbers, allowing you to divide any number by any other number (excluding division by zero).
-
Dividing decimals: Dividing decimals requires careful handling of the decimal point, but the fundamental principles remain the same.
-
Division with negative numbers: The rules for signs in division are similar to those in multiplication. A positive number divided by a positive number is positive; a negative number divided by a positive number is negative, and so on.
Frequently Asked Questions (FAQ)
Q: Why can't we divide by zero?
A: Division by zero is undefined in mathematics. Imagine trying to divide 15 items into zero groups. It's impossible; the concept lacks meaning. Dividing by a number close to zero will result in an extremely large number, highlighting the impossibility of division by zero.
Q: Which representation of the answer (mixed number, decimal, or improper fraction) is best?
A: The optimal representation depends on the context. Mixed numbers are often easiest to visualize; decimals offer precision in measurement; improper fractions are useful in algebraic manipulations. The best choice is the one that best suits the specific application.
Q: What if I get a remainder that is not a whole number?
A: It's possible to get a decimal or fractional remainder. In such instances, you might choose to convert the remainder into a decimal fraction to achieve a more precise solution.
Q: How can I improve my understanding of division?
A: Practice is key! Work through various division problems, using different methods (long division, calculator, etc.), and try to solve real-world problems that involve division.
Conclusion: Mastering Division, One Step at a Time
The seemingly simple problem of 15 divided by 4 unveils a wealth of mathematical concepts and practical applications. Understanding the different ways to represent the solution (mixed number, decimal, improper fraction) and the significance of the remainder is essential for navigating various situations in life. By mastering division, we unlock a fundamental skill that enhances our problem-solving abilities and strengthens our numerical literacy, paving the way for tackling more complex mathematical challenges in the future. So, embrace the power of division and unlock a world of numerical possibilities! Remember, the journey of mathematical understanding is a continuous process of exploration, discovery, and application. Embrace the challenges, celebrate your successes, and enjoy the fascinating world of numbers!
Latest Posts
Latest Posts
-
Is 1 2 Bigger Than 3 5
Sep 15, 2025
-
What Is 5 10 Simplified
Sep 15, 2025
-
3 5 5 As A Percent
Sep 15, 2025
-
19 3 As A Decimal
Sep 15, 2025
-
Present Value Of 1 Table
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 5 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.