1 Divided By 1 3
saludintensiva
Sep 14, 2025 · 5 min read
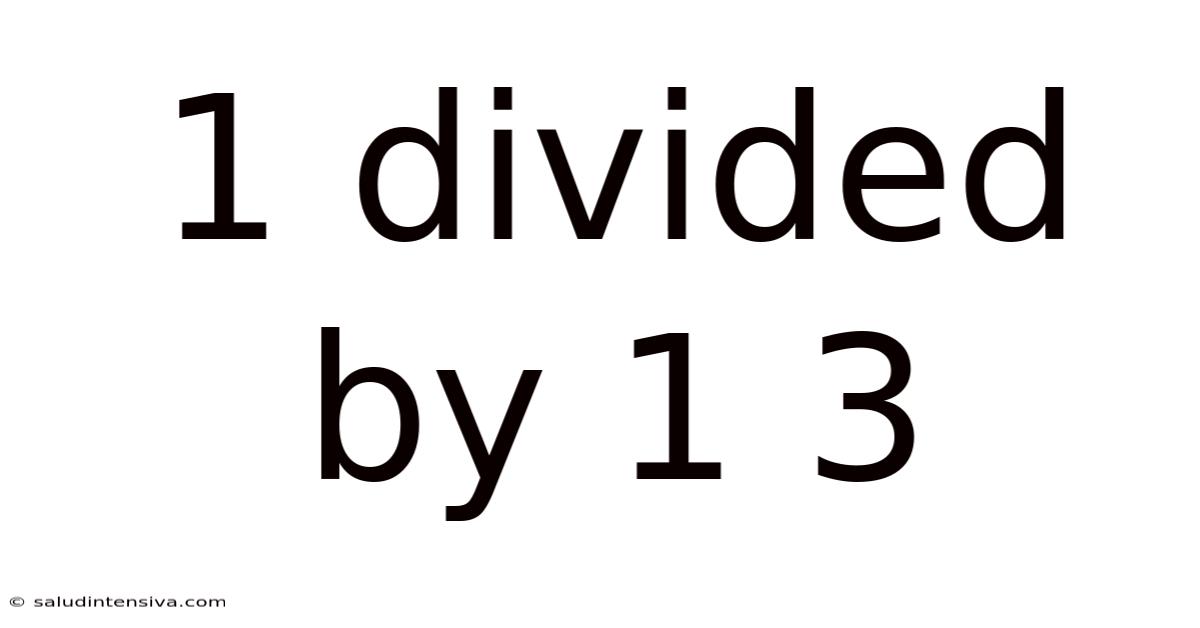
Table of Contents
Decoding 1 Divided by 1⅓: A Deep Dive into Fractions and Division
This article explores the seemingly simple yet conceptually rich problem of dividing 1 by 1⅓. We'll delve into the fundamental principles of fraction division, providing a step-by-step solution and exploring the underlying mathematical concepts. Understanding this problem unlocks a deeper appreciation of how fractions interact within arithmetic operations. This comprehensive guide will empower you to confidently tackle similar problems and solidify your understanding of fractional arithmetic.
Introduction: Understanding the Problem
The problem, 1 ÷ 1⅓, presents a common challenge for those working with fractions. At first glance, it might seem straightforward, but a solid understanding of fraction manipulation is crucial for a correct and insightful solution. This problem isn't just about finding the answer; it's about mastering the process and gaining a deeper intuition for how fractions behave. We'll break down the process meticulously, ensuring a thorough grasp of the principles involved.
Step-by-Step Solution: Converting to Improper Fractions
The first, and often most crucial, step is converting the mixed number 1⅓ into an improper fraction. A mixed number consists of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). To convert 1⅓ to an improper fraction, we multiply the whole number (1) by the denominator (3) and add the numerator (1). This sum (1 x 3 + 1 = 4) becomes the new numerator, while the denominator remains the same (3). Therefore, 1⅓ becomes ⁴⁄₃.
Our problem now transforms into 1 ÷ ⁴⁄₃. Remember that 1 can be represented as any fraction where the numerator and denominator are equal (e.g., ¹⁄₁, ²⁄₂, ³⁄₃, etc.). For consistency and ease of calculation, we'll represent 1 as ³⁄₃.
The revised problem is now ³⁄₃ ÷ ⁴⁄₃.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial step: inverting (finding the reciprocal of) the second fraction and then multiplying. The reciprocal of a fraction is simply switching the numerator and denominator. The reciprocal of ⁴⁄₃ is ³⁄₄.
So, ³⁄₃ ÷ ⁴⁄₃ becomes ³⁄₃ x ³⁄₄.
Now, we multiply the numerators together and the denominators together:
(3 x 3) / (3 x 4) = ⁹⁄₁₂
Simplifying the Fraction: Finding the Lowest Common Denominator
The resulting fraction, ⁹⁄₁₂, isn't in its simplest form. To simplify, we find the greatest common divisor (GCD) of the numerator and denominator. The GCD of 9 and 12 is 3. We then divide both the numerator and denominator by the GCD:
⁹⁄₁₂ ÷ ³⁄₃ = ³⁄₄
Therefore, 1 divided by 1⅓ equals ³⁄₄.
Visual Representation: Understanding the Concept
Imagine you have one whole pizza. You want to divide this pizza into servings of 1⅓ slices each. How many servings can you get? The answer, ³⁄₄, means you can get three-quarters of a serving from one whole pizza. This visual analogy helps to ground the abstract mathematical concept in a relatable context.
Explaining the Math: Why Does the Reciprocal Method Work?
The reciprocal method for dividing fractions might seem arbitrary, but it stems from the fundamental definition of division. Division is essentially the inverse operation of multiplication. When we divide a by b, we're asking, "What number, when multiplied by b, equals a?"
Let's consider our original problem: 1 ÷ 1⅓. Let's represent the unknown answer as x. The equation becomes:
1⅓ * x = 1
Converting 1⅓ to an improper fraction (⁴⁄₃), we have:
⁴⁄₃ * x = 1
To solve for x, we multiply both sides of the equation by the reciprocal of ⁴⁄₃, which is ³⁄₄:
³⁄₄ * ⁴⁄₃ * x = 1 * ³⁄₄
Notice that ³⁄₄ * ⁴⁄₃ simplifies to 1. This leaves:
x = ³⁄₄
This algebraic approach demonstrates why the reciprocal method works; it's a direct consequence of the inverse relationship between multiplication and division.
Beyond the Basics: Exploring Decimal Equivalents and Applications
The fraction ³⁄₄ is also easily converted to its decimal equivalent: 0.75. This equivalence highlights the flexibility of representing numbers in different forms (fractions, decimals, percentages). Understanding these interconversions is essential for applying mathematical concepts in various contexts.
This simple division problem finds applications in numerous real-world scenarios. Imagine dividing a quantity of materials, calculating proportions in recipes, or determining unit costs based on fractional measurements. The ability to efficiently and accurately handle fraction division is a valuable skill across numerous disciplines.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this problem? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for developing mathematical fluency and problem-solving skills. Calculators can verify your answer, but they don't provide the same depth of understanding.
-
Q: What if the numbers involved are more complex? A: The same principles apply. Convert all mixed numbers to improper fractions, find the reciprocal of the second fraction, multiply, and simplify the resulting fraction. The complexity increases with larger numbers, but the fundamental steps remain consistent.
-
Q: Why is simplifying fractions important? A: Simplifying fractions ensures the answer is presented in its most concise and easily understandable form. It also simplifies further calculations if the result is used in subsequent steps.
-
Q: Are there other methods to divide fractions? A: While the reciprocal method is generally the most efficient, you can also use common denominators to perform the division. However, the reciprocal method is typically faster and less prone to errors.
Conclusion: Mastering Fraction Division
The seemingly simple problem of 1 divided by 1⅓ provides a valuable learning opportunity. By working through the steps, understanding the underlying mathematical principles, and exploring different representations (fractional and decimal), we enhance our ability to confidently and accurately handle fraction division. This skill translates to success in numerous mathematical contexts and provides a strong foundation for more advanced mathematical concepts. Remember the key steps: convert to improper fractions, find the reciprocal, multiply, and simplify. With practice, you'll master this fundamental aspect of arithmetic.
Latest Posts
Latest Posts
-
What Time Is 14 55
Sep 14, 2025
-
Gcf Of 32 And 28
Sep 14, 2025
-
Gcf Of 8 And 36
Sep 14, 2025
-
4 16 As A Percent
Sep 14, 2025
-
Gcf Of 36 And 32
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.