110 Percent As A Decimal
saludintensiva
Sep 16, 2025 · 5 min read
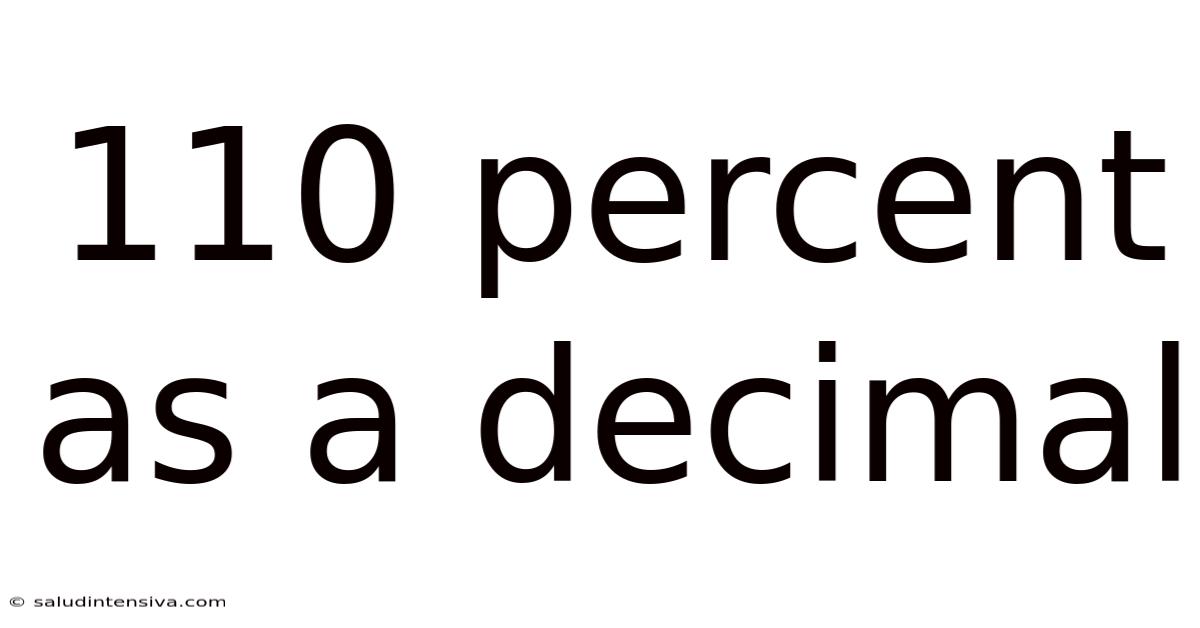
Table of Contents
110 Percent as a Decimal: Understanding Percentages and Their Decimal Equivalents
Percentages are a fundamental part of everyday life, used in everything from calculating sales tax and discounts to understanding financial reports and expressing probability. Understanding how to convert percentages to decimals, and vice versa, is a crucial skill for anyone navigating the numerical world. This article delves deep into the concept of 110% as a decimal, exploring the underlying principles and providing a comprehensive understanding of percentage-to-decimal conversions, including those exceeding 100%. We'll also explore practical applications and address common misconceptions.
Understanding Percentages and Decimals
Before diving into the specifics of 110%, let's solidify our understanding of percentages and their relationship to decimals. A percentage represents a fraction of 100. The word "percent" itself literally means "out of 100" (from the Latin per centum). Therefore, 50% means 50 out of 100, which can be written as the fraction 50/100.
Decimals, on the other hand, represent numbers based on powers of 10. They use a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents five-tenths (5/10).
The key connection between percentages and decimals lies in their shared representation of parts of a whole. To convert a percentage to a decimal, we simply divide the percentage by 100. This is because the percentage is already expressed as a fraction with a denominator of 100.
Converting Percentages to Decimals: The General Method
The process of converting any percentage to its decimal equivalent is straightforward:
-
Remove the percent sign (%): This simply leaves you with the numerical value of the percentage.
-
Divide by 100: Dividing by 100 is equivalent to moving the decimal point two places to the left.
Let's illustrate this with a few examples:
- 50%: Remove the % sign, leaving 50. Divide by 100: 50/100 = 0.50 or 0.5
- 15%: Remove the % sign, leaving 15. Divide by 100: 15/100 = 0.15
- 2.5%: Remove the % sign, leaving 2.5. Divide by 100: 2.5/100 = 0.025
110% as a Decimal: A Detailed Explanation
Now, let's apply this knowledge to the specific case of 110%. Following the steps outlined above:
-
Remove the % sign: This leaves us with 110.
-
Divide by 100: 110/100 = 1.10 or 1.1
Therefore, 110% as a decimal is 1.1. This might seem counterintuitive at first—a percentage greater than 100% resulting in a decimal greater than 1. However, this is perfectly logical. Remember, percentages represent parts of a whole, and the whole is represented by 100%. A percentage exceeding 100% signifies a quantity that is more than the whole.
Understanding Percentages Greater Than 100%
Percentages greater than 100% represent values exceeding the original whole. These percentages frequently appear in various contexts:
-
Growth and Increase: If a company's profits increase by 110%, it means its profits have more than doubled. The original profit level is considered 100%, and the additional 10% represents the increase beyond that.
-
Financial Investments: Investment returns can easily exceed 100%, signifying a significant increase in the investment's value.
-
Statistical Analysis: In some statistical measures, values exceeding 100% might indicate a significant deviation from the norm or a dramatic increase in a particular variable.
-
Overachievement: In project management or sales targets, exceeding 100% often signifies exceeding the initial goals and targets.
Practical Applications of 110% as a Decimal
The decimal equivalent of 110%, 1.1, finds application in various calculations:
-
Calculating Increases: If you need to increase a value by 110%, you multiply the original value by 1.1. For example, to increase $100 by 110%, you calculate: $100 * 1.1 = $110.
-
Finding the Total Value After an Increase: If something increased by 110%, its final value represents 210% of the original value (100% + 110%). To find the final value, you can multiply the original value by 2.1. Alternatively, you could multiply by 1.1 to find the increase and add it to the original value.
Common Misconceptions about Percentages and Decimals
Several misconceptions frequently arise regarding percentages and decimals:
-
Confusing percentages with decimals directly: Remember, you must always divide the percentage by 100 to convert it to a decimal. Simply removing the "%" sign doesn't suffice.
-
Misinterpreting percentages greater than 100%: Many people struggle to comprehend percentages exceeding 100%. Remember that these represent values greater than the whole.
-
Incorrect Calculations with Percentage Increases: It's crucial to understand that a 110% increase doesn't mean multiplying by 110. Instead, it implies multiplying by 2.1 (1 + 1.1). Simply multiplying by 1.1 correctly represents the increase added to the original amount.
Frequently Asked Questions (FAQ)
-
Q: Can a percentage be more than 100%? A: Yes, absolutely. Percentages exceeding 100% represent values larger than the original whole.
-
Q: How do I convert a decimal back to a percentage? A: Multiply the decimal by 100 and add the "%" sign.
-
Q: What is the difference between 110% and 1.10? A: They represent the same value, but in different forms. 110% is the percentage form, while 1.10 is its decimal equivalent.
-
Q: Why is it important to understand percentage-to-decimal conversion? A: This conversion is fundamental for various calculations, from simple financial transactions to complex statistical analyses. Mastering this skill is essential for numerical literacy.
-
Q: How do I calculate a percentage decrease? A: For a decrease of X%, you would multiply the original value by (1 - X/100). For example, a 20% decrease means multiplying by (1 - 0.20) = 0.80
Conclusion
Understanding the conversion between percentages and decimals is a cornerstone of numerical fluency. This article has explored the concept of 110% as a decimal, emphasizing its value as 1.1. We've also examined the broader context of percentages greater than 100%, dispelled common misconceptions, and addressed frequently asked questions. Mastering these concepts empowers you to confidently tackle various numerical challenges encountered in daily life, from personal finance to professional endeavors. Remember, the ability to seamlessly translate between percentages and decimals enhances your problem-solving skills significantly. Practice converting percentages to decimals and vice-versa regularly to solidify your understanding and build confidence in your numerical abilities.
Latest Posts
Latest Posts
-
9 Kg How Many Pounds
Sep 16, 2025
-
Negative 5 Minus Negative 7
Sep 16, 2025
-
2 3 Is Equivalent To What
Sep 16, 2025
-
Fraction From Smallest To Biggest
Sep 16, 2025
-
Is 43 Prime Or Composite
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 110 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.