13 15 As A Decimal
saludintensiva
Sep 14, 2025 · 5 min read
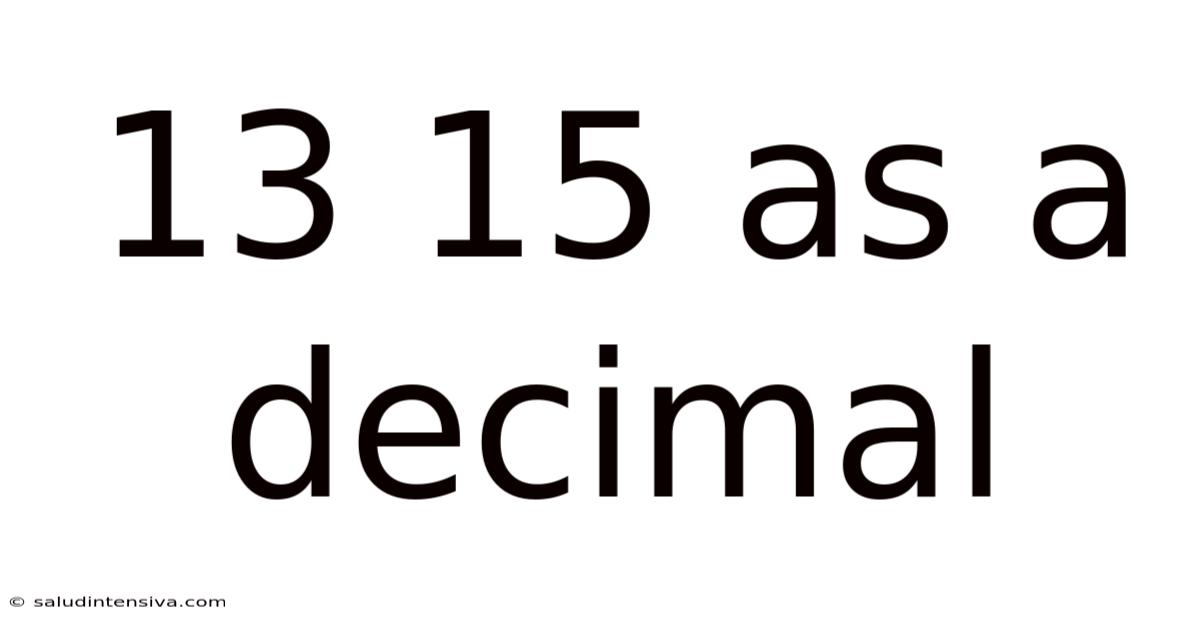
Table of Contents
Decoding 13/15 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article provides a comprehensive guide to converting the fraction 13/15 into its decimal form, exploring different methods, explaining the underlying principles, and addressing common questions. We'll delve into the process, offering a clear and step-by-step approach suitable for students and anyone looking to strengthen their understanding of fractional representation. By the end, you’ll not only know the decimal equivalent of 13/15 but also grasp the broader concepts behind decimal conversion.
Understanding Fractions and Decimals
Before diving into the conversion of 13/15, let's establish a foundational understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 13/15, 13 is the numerator and 15 is the denominator. This signifies 13 out of 15 equal parts.
A decimal, on the other hand, represents a number based on the powers of 10. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half (1/2), and 0.75 represents three-quarters (3/4). Decimals are a convenient way to express fractions, especially in calculations and measurements.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. This method involves dividing the numerator (13) by the denominator (15).
Steps:
-
Set up the division: Write 13 as the dividend (inside the division symbol) and 15 as the divisor (outside the division symbol).
-
Add a decimal point and zeros: Since 13 is smaller than 15, add a decimal point to the dividend (13) followed by as many zeros as needed to achieve the desired level of accuracy. We'll add a few zeros initially: 13.0000
-
Perform the long division: Begin dividing 15 into 130. 15 goes into 130 eight times (15 x 8 = 120). Write 8 above the first zero in the dividend.
-
Subtract: Subtract 120 from 130, leaving a remainder of 10.
-
Bring down the next zero: Bring down the next zero from the dividend, creating 100.
-
Continue dividing: 15 goes into 100 six times (15 x 6 = 90). Write 6 above the second zero in the dividend.
-
Subtract again: Subtract 90 from 100, leaving a remainder of 10.
-
Repeat the process: Notice a pattern emerging? We keep getting a remainder of 10. This indicates a repeating decimal.
-
Express the result: The decimal representation of 13/15 is 0.86666... The '6' repeats infinitely. This is often written as 0.86̅. The bar above the 6 indicates that it repeats.
Method 2: Using a Calculator
A simpler, albeit less instructive, method is to use a calculator. Simply enter 13 ÷ 15 and the calculator will display the decimal equivalent: 0.866666... or a rounded-off version depending on the calculator's settings. While convenient, this method doesn't illustrate the underlying mathematical principles involved in the conversion.
Understanding Repeating Decimals
The decimal representation of 13/15, 0.86̅, is a repeating decimal. This means the digits after the decimal point repeat in a specific pattern infinitely. Understanding why this occurs is crucial. It's because the denominator, 15, contains prime factors other than 2 and 5 (it's 3 x 5). When a fraction's denominator has prime factors other than 2 and 5, its decimal representation will be a repeating decimal. Fractions with denominators containing only 2 and/or 5 as prime factors will always result in terminating decimals (decimals that end).
Rounding the Decimal
For practical applications, we often need to round repeating decimals. The level of rounding depends on the required precision. For example:
- Rounded to two decimal places: 0.87
- Rounded to three decimal places: 0.867
- Rounded to four decimal places: 0.8667
The choice of rounding depends on the context. In engineering or scientific calculations, higher precision (more decimal places) might be necessary. In everyday situations, rounding to two decimal places is often sufficient.
Practical Applications of Decimal Conversions
Converting fractions to decimals is essential in various fields:
- Finance: Calculating percentages, interest rates, and financial ratios often requires converting fractions to decimals.
- Engineering: Precise measurements and calculations in engineering projects rely on accurate decimal representations.
- Science: Scientific data analysis often involves converting fractions to decimals for easier calculations and data visualization.
- Everyday Life: Calculating discounts, proportions, and many other daily tasks involve fraction-to-decimal conversions.
Frequently Asked Questions (FAQ)
Q1: Why does 13/15 result in a repeating decimal?
A1: Because the denominator, 15, has prime factors (3 and 5) that are not just 2 or 5. If the denominator contained only 2 and/or 5 as prime factors, the resulting decimal would terminate.
Q2: How accurate does the decimal representation need to be?
A2: The required accuracy depends entirely on the context. In some cases, rounding to two decimal places might be sufficient, while in others, several more decimal places are necessary for precision.
Q3: What if I need to convert a more complex fraction?
A3: The long division method works for any fraction. For very complex fractions, a calculator or specialized software might be more efficient.
Q4: Is there a shortcut to determine if a fraction will produce a repeating or terminating decimal?
A4: Yes, examine the denominator's prime factorization. If the denominator's only prime factors are 2 and/or 5, the decimal will terminate. Otherwise, it will repeat.
Q5: Can I convert a repeating decimal back to a fraction?
A5: Yes, there are methods to convert repeating decimals back into their fractional form. These methods typically involve algebraic manipulation.
Conclusion
Converting the fraction 13/15 to its decimal equivalent, 0.86̅, involves understanding both fractions and decimals. Long division provides a clear and understandable method, highlighting the underlying mathematical principles. While calculators offer a quicker route, understanding the process of long division is crucial for grasping the concept of repeating decimals and their significance. The accuracy needed for the decimal representation depends on the specific application. Remember, mastering this conversion skill is essential in various academic and professional fields. Hopefully, this comprehensive guide has not only provided you with the answer but also deepened your understanding of the broader mathematical concepts involved.
Latest Posts
Latest Posts
-
Area Of A Hollow Pipe
Sep 14, 2025
-
How To Get Common Factor
Sep 14, 2025
-
Whats Bigger 3 8 Or 7 16
Sep 14, 2025
-
Lcm Of 32 And 40
Sep 14, 2025
-
Lcm Of 17 And 13
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 13 15 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.