17 4 As A Decimal
saludintensiva
Sep 14, 2025 · 6 min read
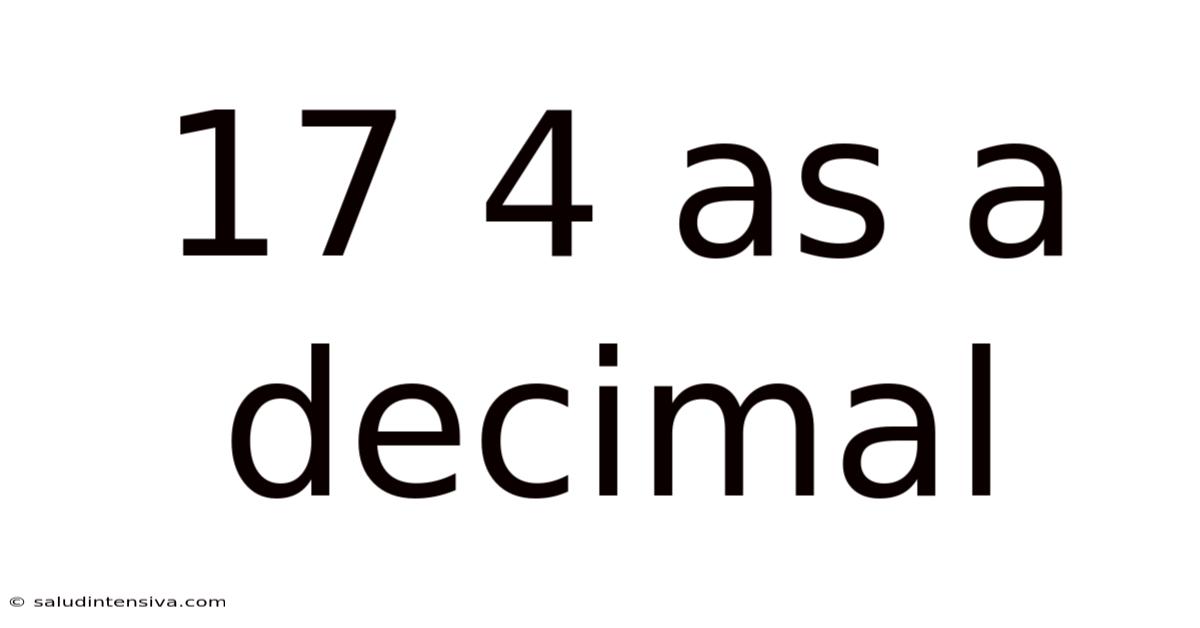
Table of Contents
Decoding 17/4 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the fraction 17/4 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying concepts. We'll delve into the practical applications of this conversion and address frequently asked questions. By the end, you'll not only know the answer but also possess the tools to tackle similar conversions with confidence.
Understanding Fractions and Decimals
Before we dive into the conversion of 17/4, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, is a way of representing a number using base-10, where the position of each digit represents a power of 10. The decimal point separates the whole number part from the fractional part. For example, in the decimal 12.34, 12 represents the whole number part, while .34 represents the fractional part (3/10 + 4/100).
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. In this method, we divide the numerator by the denominator.
Steps:
-
Set up the long division: Write the numerator (17) inside the long division symbol and the denominator (4) outside.
-
Divide: Ask yourself, "How many times does 4 go into 17?" The answer is 4 (because 4 x 4 = 16). Write the 4 above the 7 in the dividend (17).
-
Multiply: Multiply the quotient (4) by the divisor (4): 4 x 4 = 16. Write this below the 17.
-
Subtract: Subtract the result (16) from the dividend (17): 17 - 16 = 1.
-
Bring down: Since we have a remainder (1), we bring down a zero (adding a decimal point and a zero to the dividend). This becomes 10.
-
Repeat: Ask yourself, "How many times does 4 go into 10?" The answer is 2 (because 4 x 2 = 8). Write the 2 after the decimal point in the quotient.
-
Multiply and Subtract: Multiply the new digit (2) by the divisor (4): 2 x 4 = 8. Subtract this from 10: 10 - 8 = 2.
-
Continue the process: Bring down another zero to get 20. 4 goes into 20 five times (4 x 5 = 20). Subtract 20 from 20, resulting in a remainder of 0.
Therefore, 17/4 = 4.25
Method 2: Converting to an Improper Fraction (If Necessary)
If the fraction is an improper fraction (numerator is greater than the denominator), as in this case, you can directly proceed with long division as shown above. However, if you have a mixed number, you must first convert it into an improper fraction before performing long division. A mixed number is a combination of a whole number and a proper fraction (e.g., 4 1/4).
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Keep the same denominator.
For example, 4 1/4 would become (4 x 4) + 1 / 4 = 17/4. Then you proceed with long division as demonstrated above.
Method 3: Using Decimal Equivalents of Common Fractions
Knowing the decimal equivalents of some common fractions can help in quicker conversions. For instance:
- 1/4 = 0.25
- 1/2 = 0.5
- 3/4 = 0.75
While this method is less applicable directly to 17/4, understanding these equivalents assists in estimations and mental calculations. You can think of 17/4 as 4 + 1/4, making the conversion to 4.25 relatively intuitive if you are familiar with the decimal equivalent of 1/4.
The Scientific Explanation: Base-10 Representation
The conversion from a fraction to a decimal is fundamentally about changing the base of representation from a fractional base (where the denominator dictates the size of the parts) to a base-10 system (decimal). Long division effectively performs this conversion by repeatedly dividing the numerator by the denominator until we reach a remainder of zero or a repeating pattern. The decimal places represent the successive division of the remainder by the denominator, expressing the fraction in terms of tenths, hundredths, thousandths, and so on.
Practical Applications of Decimal Conversions
Converting fractions to decimals is a crucial skill in numerous real-world applications:
- Financial Calculations: Working with percentages, interest rates, and monetary values often requires decimal representations.
- Measurement and Engineering: Precise measurements in various fields, such as engineering and construction, use decimals extensively.
- Scientific Calculations: Many scientific formulas and calculations require decimal representations for accurate results.
- Data Analysis: In statistics and data analysis, decimals are used for representing probabilities, averages, and other statistical measures.
- Computer Programming: Computers internally work with binary (base-2) representation, but decimal representation is vital for user input and output.
Frequently Asked Questions (FAQ)
Q: What if the long division results in a repeating decimal?
A: Some fractions result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can represent the repeating part using a bar over the repeating digits (e.g., 0.3̅).
Q: Are there other methods to convert fractions to decimals?
A: While long division is the most common method, there are other less frequently used methods involving conversion to equivalent fractions with denominators as powers of 10 (10, 100, 1000, etc.). However, long division remains a robust and widely applicable approach.
Q: Can I use a calculator for this conversion?
A: Yes, calculators can quickly convert fractions to decimals. Simply enter the fraction (17/4) and press the equals (=) button. However, understanding the process of long division is crucial for building a strong mathematical foundation.
Q: Why is it important to learn this conversion method?
A: Mastering fraction-to-decimal conversion enhances your mathematical understanding, problem-solving abilities, and practical skills applicable across diverse fields. It improves your numerical fluency and allows you to confidently work with both fractions and decimals.
Conclusion
Converting 17/4 to its decimal equivalent, 4.25, is a fundamental exercise showcasing the interplay between fractions and decimals. By employing long division, you not only obtain the answer but also gain a deeper understanding of the underlying mathematical principles. This understanding extends beyond simple conversions, empowering you to confidently tackle more complex problems and navigate various numerical situations effectively. Remember that practicing different methods and exploring varied approaches strengthens your mathematical proficiency and enhances your problem-solving skills.
Latest Posts
Latest Posts
-
2 2 8 As A Decimal
Sep 14, 2025
-
90 Percent As A Decimal
Sep 14, 2025
-
Convert 7 To A Decimal
Sep 14, 2025
-
6 5 M 1 26
Sep 14, 2025
-
Whats Equivalent To 2 4
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 17 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.