18/5 As A Mixed Number
saludintensiva
Sep 20, 2025 · 6 min read
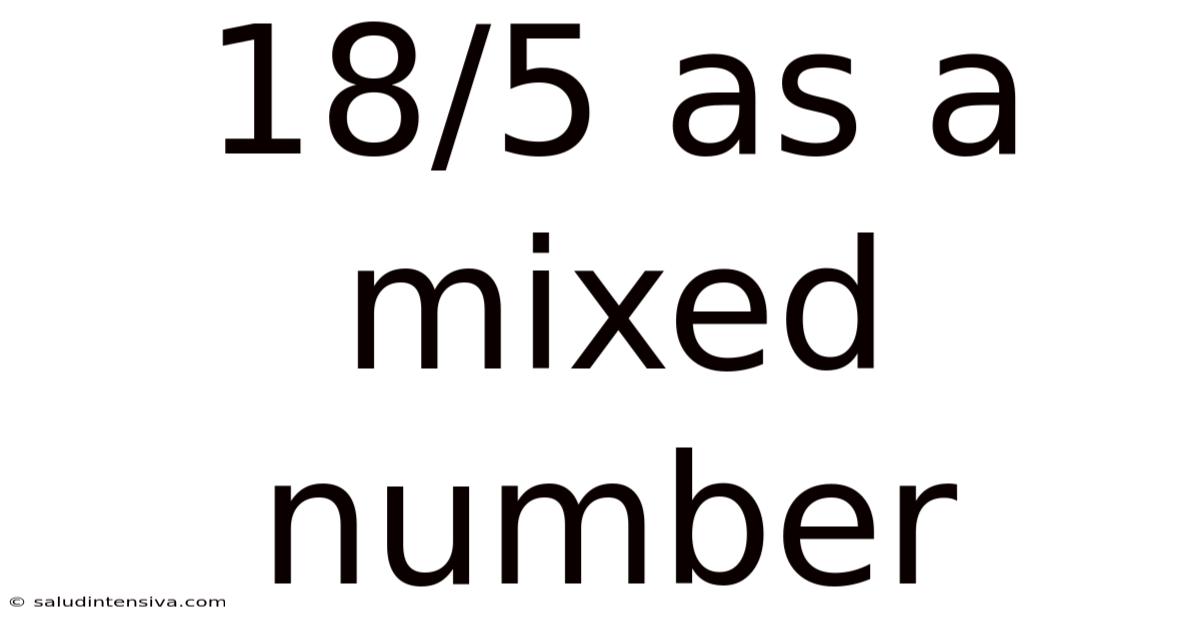
Table of Contents
Understanding 18/5 as a Mixed Number: A Comprehensive Guide
The concept of mixed numbers is fundamental in arithmetic and forms a crucial bridge between fractions and whole numbers. This article will delve deeply into understanding how to represent the improper fraction 18/5 as a mixed number, explaining the process in detail, exploring the underlying mathematical principles, and addressing common questions and misconceptions. We will cover various methods, ensuring a comprehensive understanding for learners of all levels. Mastering this concept is essential for success in further mathematical studies and real-world applications.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1/2, 3/4, and 5/8 are all proper fractions. A mixed number represents a value greater than one. For instance, 1 ½ (one and a half) is a mixed number; it represents one whole unit and half of another. Understanding mixed numbers is critical for solving many math problems involving measurements, quantities, and proportions.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 18/5 is an improper fraction because the numerator (18) is greater than the denominator (5). To convert an improper fraction like 18/5 into a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is.
Method 1: Long Division
The most straightforward method involves long division. We divide the numerator (18) by the denominator (5):
3
5 | 18
15
3
The quotient (the result of the division) is 3, and the remainder is 3. This means that 5 goes into 18 three times with a remainder of 3. Therefore, the mixed number representation of 18/5 is 3 3/5. The whole number part is the quotient (3), and the fractional part is the remainder (3) over the original denominator (5).
Method 2: Repeated Subtraction
This method is particularly helpful for visualizing the concept. We repeatedly subtract the denominator from the numerator until we reach a number less than the denominator.
- Start with the numerator: 18
- Subtract the denominator: 18 - 5 = 13
- Subtract the denominator again: 13 - 5 = 8
- Subtract the denominator again: 8 - 5 = 3
We subtracted the denominator (5) three times before reaching a remainder less than 5. The number of times we subtracted (3) is the whole number part of our mixed number. The remainder (3) becomes the numerator of the fraction, and the denominator remains 5. Therefore, 18/5 = 3 3/5.
Method 3: Understanding the Concept of "Groups"
Think of 18/5 as representing 18 items divided into groups of 5. How many full groups of 5 can we make from 18 items? We can make three full groups (3 x 5 = 15). This leaves us with 18 - 15 = 3 items remaining. These 3 remaining items represent the fraction part of our mixed number, still divided into groups of 5, resulting in 3/5. Therefore, 18/5 = 3 3/5.
Visual Representation
Imagine you have 18 pizzas, and you want to divide them among 5 friends equally. Each friend would receive 3 whole pizzas (3 x 5 = 15 pizzas). You'll have 3 pizzas left over. These 3 pizzas will be divided among the 5 friends, resulting in each friend getting an additional 3/5 of a pizza. Again, this visually demonstrates why 18/5 equals 3 3/5.
Converting Mixed Numbers Back to Improper Fractions
It's essential to understand the reverse process as well. To convert a mixed number (like 3 3/5) back to an improper fraction, follow these steps:
- Multiply: Multiply the whole number (3) by the denominator (5): 3 x 5 = 15
- Add: Add the result to the numerator (3): 15 + 3 = 18
- Keep the denominator: The denominator remains the same (5).
Therefore, 3 3/5 becomes 18/5. This confirms the accuracy of our earlier conversions.
The Importance of Understanding Mixed Numbers
Mixed numbers are crucial in various real-world scenarios:
- Measurement: Expressing lengths, weights, or volumes often involves mixed numbers. For example, 2 1/2 feet or 3 3/4 inches.
- Cooking/Baking: Recipes frequently use mixed numbers to specify ingredient quantities.
- Construction/Engineering: Accurate measurements are vital, and mixed numbers help in precise calculations.
- Finance: Dealing with fractional shares or portions of investments often involves mixed numbers.
Furthermore, a firm grasp of mixed numbers is essential for progressing to more advanced mathematical concepts, including:
- Algebra: Solving equations involving fractions and mixed numbers.
- Geometry: Calculations involving areas, volumes, and perimeters may involve mixed numbers.
- Calculus: The foundations of calculus build upon a strong understanding of fractions and mixed numbers.
Frequently Asked Questions (FAQs)
Q: Can all improper fractions be converted into mixed numbers?
A: Yes, every improper fraction can be converted into a mixed number, except for those where the numerator is a multiple of the denominator (e.g., 10/5, which simplifies to 2). In such cases, the result is a whole number.
Q: What if the remainder is zero after the division?
A: If the remainder is zero, it means the improper fraction is already a whole number. For instance, 20/5 = 4. There is no fractional part in the mixed number representation.
Q: Are there other ways to represent 18/5 besides 3 3/5?
A: No, 3 3/5 is the simplest and most common way to represent 18/5 as a mixed number. While you could technically express it as other equivalent fractions (e.g., converting 3/5 to 6/10, resulting in 3 6/10), it would not be the simplest form.
Q: Why is it important to learn this concept?
A: Understanding mixed numbers is fundamental for practical applications and building a strong mathematical foundation. It enables you to confidently solve problems involving fractions, measurements, and various real-world situations, paving the way for success in further mathematical studies.
Conclusion
Converting an improper fraction like 18/5 into a mixed number is a fundamental skill in mathematics. This article has provided various methods—long division, repeated subtraction, and the "groups" approach—each offering a unique perspective on this essential concept. Understanding these methods allows for flexibility and deeper comprehension, improving problem-solving abilities. The ability to seamlessly convert between improper fractions and mixed numbers is crucial for success in various mathematical contexts and real-world applications. Remember to practice these methods regularly to build confidence and proficiency. Mastering this skill will significantly enhance your mathematical abilities and open doors to more advanced concepts.
Latest Posts
Latest Posts
-
What Is 13 Degrees C
Sep 20, 2025
-
43 50 As A Percent
Sep 20, 2025
-
25 In Fraction Simplest Form
Sep 20, 2025
-
Pixels Per Inch For Print
Sep 20, 2025
-
X Sqrt 1 X 2
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 18/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.