2/1 As A Whole Number
saludintensiva
Sep 21, 2025 · 7 min read
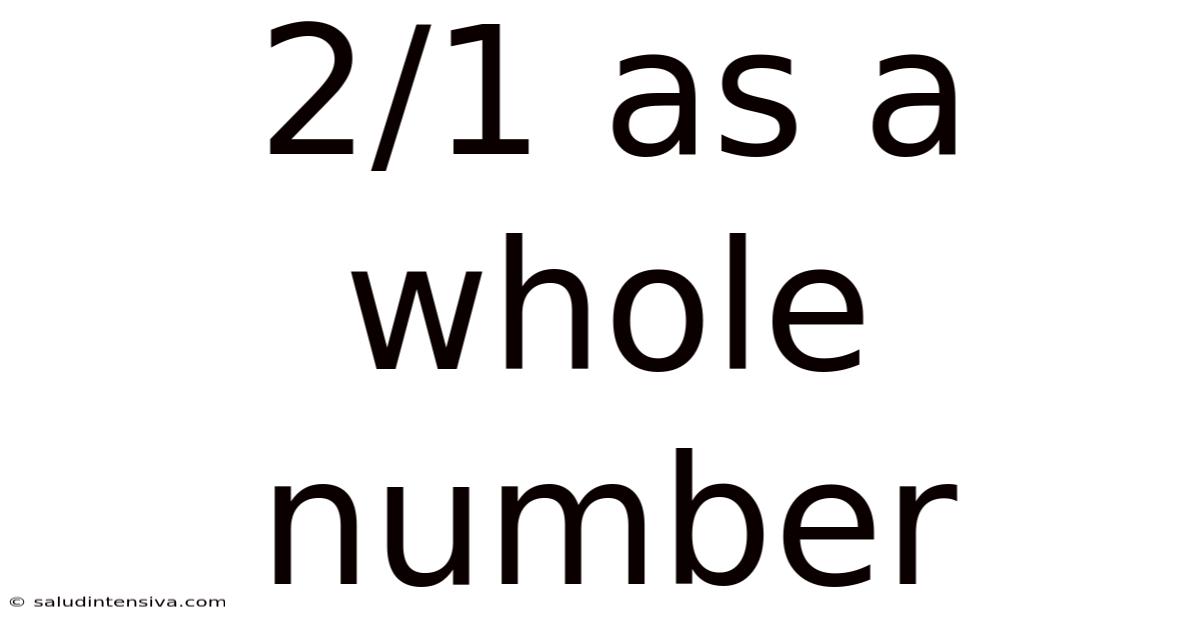
Table of Contents
Understanding 2/1 as a Whole Number: A Comprehensive Guide
The fraction 2/1 might seem deceptively simple at first glance. After all, it’s just two divided by one. However, understanding 2/1 and its representation as a whole number unlocks a deeper understanding of fractions, division, and their relationship to the number system as a whole. This comprehensive guide will explore 2/1, explain its equivalence to the whole number 2, and delve into the underlying mathematical principles. We'll cover various perspectives, addressing potential misconceptions and solidifying your grasp of this fundamental concept.
Introduction: What is a Fraction?
Before we dive into the specifics of 2/1, let's establish a solid understanding of fractions. A fraction represents a part of a whole. It’s written in the form a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For instance, 1/2 represents one out of two equal parts, while 3/4 represents three out of four equal parts.
Fractions can represent numbers less than one (proper fractions like 1/2), equal to one (improper fractions like 3/3), or greater than one (improper fractions like 5/4). Improper fractions, where the numerator is greater than or equal to the denominator, can always be converted into mixed numbers (a combination of a whole number and a proper fraction) or whole numbers.
2/1: Deconstructing the Fraction
Now, let's analyze 2/1. The numerator is 2, and the denominator is 1. This means we have two parts out of a total of one part. This might seem paradoxical at first. How can we have two parts when there's only one whole?
The key lies in understanding that the denominator represents how many equal parts the whole is divided into. In this case, the whole is not divided at all; it remains a single, undivided unit. We have two of these undivided units.
Converting 2/1 to a Whole Number: The Division Process
The process of converting 2/1 to a whole number involves performing the division indicated by the fraction. 2/1 is essentially 2 ÷ 1. Any number divided by 1 equals itself. Therefore:
2 ÷ 1 = 2
This clearly demonstrates that 2/1 is equivalent to the whole number 2. It represents two complete units, not a fraction of a unit.
Visual Representation: Understanding the Concept
Visual aids can greatly enhance understanding. Imagine you have two apples. You can represent this as a fraction by considering each apple as a whole unit. You have two whole units, which can be expressed as 2/1. The denominator, 1, indicates that we're dealing with whole units, and the numerator, 2, indicates that we have two of them. There's no division of the apples into smaller parts.
Similarly, consider a pizza. If you have two whole pizzas, you can represent this as 2/1. You have two whole units (pizzas) out of one possible whole unit (a single pizza being the reference).
Mathematical Proof and Properties
The equivalence of 2/1 and 2 can be mathematically proven using the fundamental properties of fractions and division.
-
Multiplicative Identity: Any number multiplied by 1 remains unchanged. This is the multiplicative identity property. So, 2 x 1 = 2.
-
Reciprocal: The reciprocal of a number is 1 divided by that number. The reciprocal of 1 is 1/1 = 1.
-
Division as Multiplication by the Reciprocal: Dividing by a number is equivalent to multiplying by its reciprocal. Therefore, 2 ÷ 1 is the same as 2 x (1/1) = 2 x 1 = 2.
These properties demonstrate the mathematical validity of the conversion of 2/1 to 2.
Expanding the Concept: Other Fractions with a Denominator of 1
The concept extends beyond 2/1. Any integer 'n' can be expressed as a fraction with a denominator of 1: n/1. This is because dividing any integer by 1 always results in the original integer. For example:
- 5/1 = 5
- 10/1 = 10
- 100/1 = 100
- -3/1 = -3
This reveals the fundamental relationship between integers and fractions, demonstrating how integers are a subset of the rational numbers (numbers that can be expressed as a fraction).
Practical Applications: Real-World Examples
The concept of 2/1 (and similar fractions with a denominator of 1) is not just an abstract mathematical idea. It has practical applications in various scenarios:
-
Counting Objects: If you have two books, you can represent this as 2/1. You have two complete units (books) out of one possible unit (a single book as a reference).
-
Measurement: If you measure 2 meters of fabric, you can express it as 2/1 meters. This represents two complete meters.
-
Data Representation: In computer science, data structures might involve representing quantities as fractions. 2/1 could represent two complete data packets.
-
Recipe Quantities: If a recipe calls for two cups of flour, this could conceptually be seen as 2/1 cups.
These examples highlight the relevance of understanding 2/1 as a whole number in various contexts beyond the classroom.
Addressing Common Misconceptions
Some learners might struggle with the concept of 2/1 initially, possibly due to the following misconceptions:
-
Confusion with Division: They might incorrectly think that the fraction represents dividing two into one equal parts, which is not the case. The denominator represents how many equal parts the whole is divided into; here, the whole is not divided.
-
Incorrect Visualization: They might struggle to visualize a situation where the denominator is 1. Using concrete examples like apples or pizzas, as described earlier, can help overcome this hurdle.
-
Overemphasis on Proper Fractions: A heavy focus on proper fractions (numerator < denominator) can sometimes make understanding improper fractions, including 2/1, more challenging.
Frequently Asked Questions (FAQ)
Q1: Is 2/1 the only way to represent the number 2 as a fraction?
No. There are infinitely many ways to represent 2 as a fraction. For example, 4/2, 6/3, 8/4, and so on. All these fractions are equivalent to 2 because they simplify to 2/1.
Q2: Why is the denominator important in a fraction?
The denominator tells us the total number of equal parts the whole is divided into. It is crucial in determining the size or value of the fraction. Without the denominator, we wouldn't know what the numerator refers to.
Q3: Can any whole number be represented as a fraction with a denominator of 1?
Yes, absolutely. Any whole number n can be expressed as n/1. This highlights the seamless transition from whole numbers to the broader set of rational numbers.
Q4: What is the difference between a proper fraction and an improper fraction?
A proper fraction has a numerator smaller than its denominator (e.g., 1/2, 3/4). An improper fraction has a numerator greater than or equal to its denominator (e.g., 5/4, 2/1). Improper fractions can be converted into mixed numbers or whole numbers.
Q5: Is it correct to say that 2/1 simplifies to 2?
Yes, it's perfectly correct to say that 2/1 simplifies to 2. Simplifying a fraction means expressing it in its lowest terms, and in this case, the simplest form of 2/1 is the whole number 2.
Conclusion: Mastering the Fundamentals
Understanding 2/1 as a whole number is a crucial stepping stone in mastering fundamental mathematical concepts. It bridges the gap between whole numbers and fractions, demonstrating their interconnectedness and highlighting the importance of the denominator in defining the value of a fraction. By grasping this concept, you build a stronger foundation for more advanced mathematical studies, from algebra to calculus. Remember the visual representations, the mathematical principles, and the practical applications. With consistent practice and a clear understanding of the underlying principles, you'll confidently navigate the world of fractions and beyond.
Latest Posts
Latest Posts
-
Factor X 2 4x 6
Sep 21, 2025
-
Is 3 4 Larger Than 3 8
Sep 21, 2025
-
46 Repeating As A Fraction
Sep 21, 2025
-
80 Degrees F To Celsius
Sep 21, 2025
-
X 5 X 7 Simplify
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2/1 As A Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.