2 3/8 As A Decimal
saludintensiva
Sep 13, 2025 · 6 min read
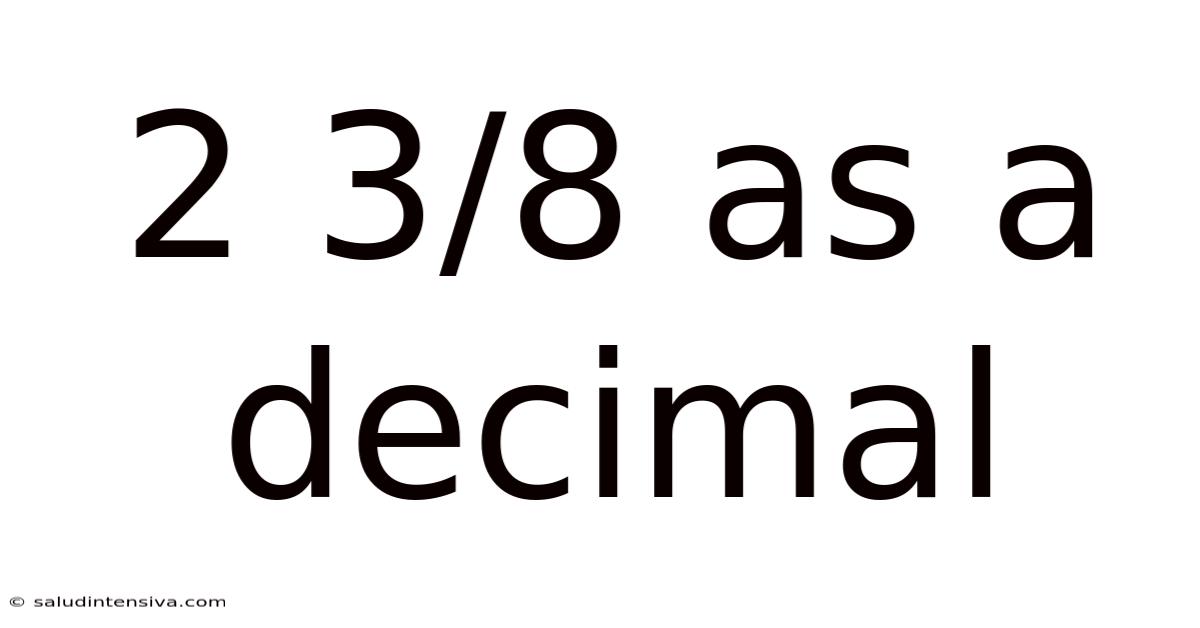
Table of Contents
2 3/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the mixed number 2 3/8 into its decimal equivalent, explaining the underlying principles and providing practical examples. We'll cover different methods, address common misconceptions, and delve into the practical significance of this conversion. By the end, you'll not only know the decimal equivalent of 2 3/8 but also understand the broader concept of fraction-to-decimal conversion.
Understanding Mixed Numbers and Fractions
Before we dive into the conversion, let's briefly review the terminology. A mixed number combines a whole number and a fraction, like 2 3/8. The whole number (2 in this case) represents whole units, while the fraction (3/8) represents a part of a whole unit. The fraction itself consists of a numerator (3) and a denominator (8). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward method. We'll first convert the fraction 3/8 into a decimal and then add the whole number 2.
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case:
3 ÷ 8 = 0.375
Now, we add the whole number:
2 + 0.375 = 2.375
Therefore, 2 3/8 as a decimal is 2.375.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed number into an improper fraction, then dividing the numerator by the denominator to obtain the decimal equivalent.
To convert a mixed number to an improper fraction, we multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same.
For 2 3/8:
(2 * 8) + 3 = 19
So, the improper fraction is 19/8.
Now, we divide the numerator by the denominator:
19 ÷ 8 = 2.375
Again, we arrive at the same answer: 2 3/8 as a decimal is 2.375.
Method 3: Using Long Division (for deeper understanding)
While the previous methods are quicker, performing long division provides a deeper understanding of the conversion process. Let's illustrate this method:
-
Set up the long division problem: 8 | 19 (19 divided by 8)
-
Since 8 goes into 19 two times (8 x 2 = 16), write a "2" above the 9.
-
Subtract 16 from 19, leaving a remainder of 3.
-
Add a decimal point and a zero to the remainder (3 becomes 30).
-
Now, 8 goes into 30 three times (8 x 3 = 24). Write a "3" after the decimal point in the quotient.
-
Subtract 24 from 30, leaving a remainder of 6.
-
Add another zero (6 becomes 60).
-
8 goes into 60 seven times (8 x 7 = 56). Write a "7" after the "3" in the quotient.
-
Subtract 56 from 60, leaving a remainder of 4.
-
Add another zero (4 becomes 40).
-
8 goes into 40 five times (8 x 5 = 40). Write a "5" after the "7" in the quotient.
-
The remainder is 0, indicating the division is complete.
Therefore, the decimal equivalent of 19/8 (and thus 2 3/8) is 2.375. This method, although more time-consuming, highlights the step-by-step process of converting a fraction into its decimal form.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is essential in many real-world scenarios:
-
Financial Calculations: Dealing with money often involves fractions (e.g., calculating discounts, interest rates, or splitting bills). Converting fractions to decimals simplifies these calculations.
-
Measurement and Engineering: Precise measurements in construction, engineering, and manufacturing often require decimal precision. Converting fractional measurements into decimals allows for accurate calculations and designs.
-
Scientific Computations: Many scientific formulas and calculations require decimal representation of numbers for accurate results.
-
Data Analysis and Statistics: Data analysis often involves working with numerical data, and converting fractions to decimals allows for easier manipulation and interpretation of the data using statistical software.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals (decimals that end)?
A: No. Fractions can be converted to either terminating decimals or repeating decimals. Terminating decimals have a finite number of digits after the decimal point, while repeating decimals have a sequence of digits that repeat infinitely. A fraction can be converted to a terminating decimal only if its denominator (in simplest form) contains only factors of 2 and/or 5. Since the denominator of 3/8 (which is 8 = 2 x 2 x 2) only contains factors of 2, it converts to a terminating decimal.
Q: What if I have a more complex mixed number?
A: The methods described above apply to any mixed number. Simply follow the steps, ensuring careful calculation. For example, to convert 5 17/25 to a decimal, you would first convert 17/25 to a decimal (17 ÷ 25 = 0.68) and then add the whole number 5 (5 + 0.68 = 5.68).
Q: Are there any online tools or calculators for fraction-to-decimal conversion?
A: Yes, many online calculators and tools are available to convert fractions to decimals quickly. However, understanding the underlying principles is crucial for solving problems independently and building a solid mathematical foundation.
Q: Why is it important to learn this skill?
A: Mastering fraction-to-decimal conversion enhances your overall mathematical proficiency. It’s a fundamental skill that enables you to tackle more complex mathematical problems across various fields of study and real-world applications. It’s a gateway to a deeper understanding of numbers and their representation.
Conclusion
Converting 2 3/8 to its decimal equivalent (2.375) is a straightforward process, easily achievable using several methods. This seemingly simple conversion demonstrates a crucial mathematical concept with broad applications. Understanding the underlying principles—and practicing different conversion techniques—will significantly enhance your mathematical skills and prepare you for more advanced mathematical concepts. By mastering this fundamental skill, you'll gain confidence in your mathematical abilities and equip yourself to tackle more complex numerical challenges with ease. Remember, the key is not just to get the answer but to understand why the answer is what it is. This understanding will serve as a foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
Lcm Of 18 And 8
Sep 13, 2025
-
What Percent Is 12 20
Sep 13, 2025
-
Is 13 Prime Or Composite
Sep 13, 2025
-
How Many Minutes Is 70
Sep 13, 2025
-
7 Percent Of 30 Hourrs
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.