What Percent Is 12 20
saludintensiva
Sep 13, 2025 · 5 min read
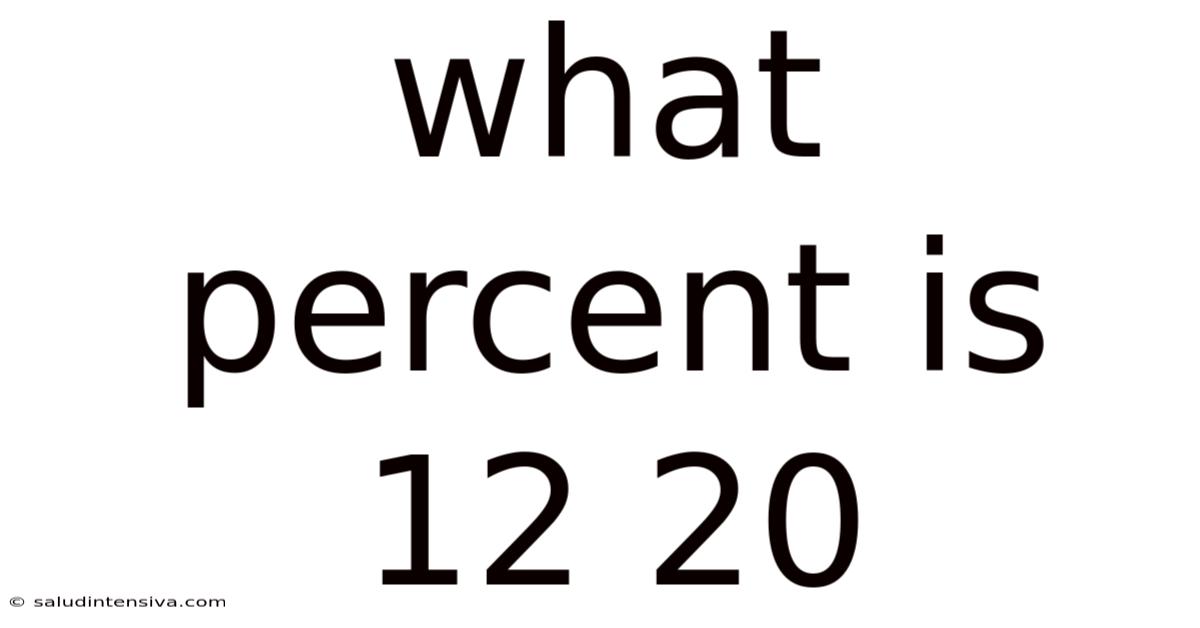
Table of Contents
What Percent is 12 of 20? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and taxes to interpreting statistics and analyzing data. This article will explore how to determine what percent 12 is of 20, providing a step-by-step guide, explaining the underlying mathematical principles, and showcasing practical examples to solidify your understanding. We'll also delve into the broader context of percentage calculations, addressing common misconceptions and frequently asked questions.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, ratios, and changes in quantities.
Calculating "What Percent is 12 of 20?"
To find what percent 12 is of 20, we need to follow a simple three-step process:
Step 1: Set up a Fraction
First, express the problem as a fraction: 12/20. This represents 12 out of 20.
Step 2: Convert the Fraction to a Decimal
Next, divide the numerator (12) by the denominator (20):
12 ÷ 20 = 0.6
Step 3: Convert the Decimal to a Percentage
Finally, multiply the decimal by 100 to convert it to a percentage:
0.6 x 100 = 60%
Therefore, 12 is 60% of 20.
Detailed Explanation: The Mathematical Principles
The process described above relies on the fundamental relationship between fractions, decimals, and percentages. Let's break it down further:
-
Fractions: A fraction represents a part of a whole. In our example, 12/20 represents 12 parts out of a total of 20 parts.
-
Decimals: A decimal is another way of expressing a fraction, where the denominator is a power of 10 (e.g., 10, 100, 1000). Converting a fraction to a decimal involves dividing the numerator by the denominator.
-
Percentages: A percentage is a fraction where the denominator is always 100. Converting a decimal to a percentage simply involves multiplying by 100 and adding the "%" symbol.
The conversion between these three forms is crucial for understanding and manipulating numerical data. Being fluent in these conversions allows for efficient problem-solving in various contexts.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is essential in many everyday situations:
-
Shopping: Calculating discounts, sales tax, and tips. For example, if a shirt costs $20 and is on sale for 20% off, you'd save $4 (20% of $20).
-
Finance: Understanding interest rates, loan repayments, and investment returns. A 5% interest rate on a savings account means your money grows by 5% annually.
-
Statistics: Interpreting data presented as percentages, such as survey results, demographic information, and economic indicators. Understanding that 60% of respondents preferred a particular product provides valuable market insights.
-
Science: Expressing concentrations, probabilities, and experimental results. For instance, a solution containing 12 grams of solute in 20 grams of solution has a concentration of 60% (w/w).
-
Education: Calculating grades, test scores, and progress reports. Achieving 12 out of 20 questions correct on an exam translates to a 60% score.
Beyond the Basics: More Complex Percentage Calculations
While the example of calculating what percent 12 is of 20 is straightforward, percentage calculations can become more complex. Here are a few variations:
-
Finding a Percentage of a Number: This involves multiplying a number by the percentage expressed as a decimal. For example, finding 60% of 50 is 50 x 0.60 = 30.
-
Finding the Original Number: If you know the percentage and the resulting value, you can find the original number. For example, if 60% of a number is 12, the number is 12 / 0.60 = 20.
-
Percentage Change: Calculating the percentage increase or decrease between two numbers. The formula is [(New Value - Old Value) / Old Value] x 100%.
Common Misconceptions about Percentages
Several misconceptions surrounding percentages can lead to errors in calculations and interpretations:
-
Adding Percentages Directly: You cannot simply add percentages directly unless they are applied to the same base value. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting Percentage Points: Percentage points refer to the absolute difference between two percentages, not the relative change. For instance, an increase from 10% to 20% is a 10-percentage-point increase, but a 100% relative increase.
-
Ignoring the Base Value: The base value to which the percentage is applied is crucial. A 10% increase on a larger number will result in a larger absolute increase than a 10% increase on a smaller number.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate percentages quickly without a calculator?
-
A: For simple percentages like 10%, 25%, and 50%, you can use mental math techniques such as dividing by 10, dividing by 4, or dividing by 2 respectively. For other percentages, you can use estimation techniques or break down the percentage into simpler components.
-
Q: What are the applications of percentages in data analysis?
-
A: Percentages are used extensively in data analysis to represent proportions, trends, and changes in data. They allow for comparisons between different datasets and provide insights into the distribution of variables.
-
Q: How do I convert a fraction to a percentage?
-
A: Divide the numerator by the denominator to get a decimal. Then, multiply the decimal by 100 and add the "%" symbol.
-
Q: How do I convert a percentage to a decimal?
-
A: Divide the percentage by 100. For example, 60% becomes 0.60.
-
Q: How do I convert a percentage to a fraction?
-
A: Write the percentage as a fraction with 100 as the denominator. Then simplify the fraction to its lowest terms. For example, 60% is 60/100, which simplifies to 3/5.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not just a mathematical skill; it's a life skill. From managing personal finances to making informed decisions in professional and academic settings, the ability to accurately calculate and interpret percentages empowers you to navigate the world more effectively. By mastering the fundamental concepts and practicing various applications, you can build confidence in your numerical abilities and unlock opportunities for growth and success. The simple calculation of "what percent is 12 of 20?" serves as a gateway to a deeper understanding of this essential mathematical concept and its far-reaching implications. Remember to practice regularly and explore different scenarios to solidify your understanding and become proficient in percentage calculations.
Latest Posts
Latest Posts
-
1 6 Is Equal To
Sep 13, 2025
-
Gcf Of 12 And 40
Sep 13, 2025
-
Equivalent Fraction Of 3 6
Sep 13, 2025
-
0 25 Acres In Square Feet
Sep 13, 2025
-
6 5 As A Percentage
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 12 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.