Lcm Of 18 And 8
saludintensiva
Sep 13, 2025 · 6 min read
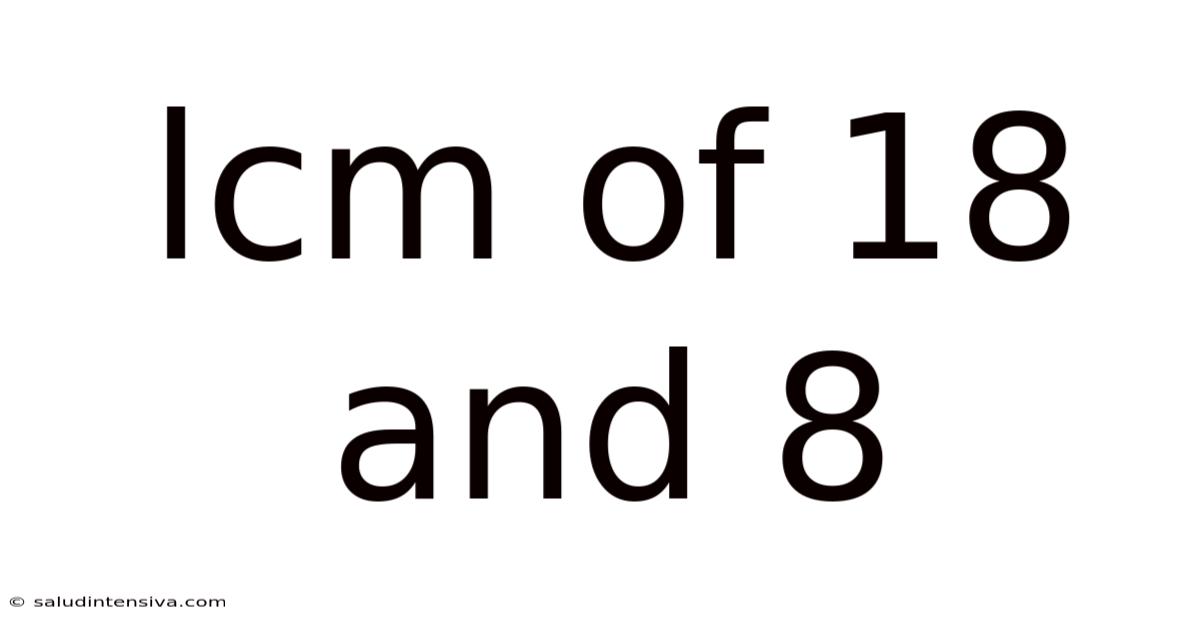
Table of Contents
Finding the LCM of 18 and 8: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical applications. This article will explore the LCM of 18 and 8 in detail, providing multiple methods for calculating it and explaining the broader significance of least common multiples in various mathematical contexts. We'll go beyond a simple answer and delve into why this calculation matters and how it applies to real-world problems.
Understanding Least Common Multiples (LCM)
Before we dive into the specifics of finding the LCM of 18 and 8, let's establish a clear understanding of what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both of your original numbers can divide into evenly. This concept is crucial in various areas, from simplifying fractions to solving problems involving cycles or periodic events.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The most straightforward approach, especially for smaller numbers like 18 and 8, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192...
Notice that 72 appears in both lists. While larger common multiples exist (144, 216, etc.), 72 is the smallest. Therefore, the LCM of 18 and 8 is 72. This method is easy to visualize but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic method, especially for larger numbers, involves using prime factorization. This method involves breaking down each number into its prime factors – the smallest prime numbers that multiply to give the original number.
- Prime Factorization of 18: 18 = 2 x 3 x 3 = 2 x 3²
- Prime Factorization of 8: 8 = 2 x 2 x 2 = 2³
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
To find the LCM, we multiply these highest powers together: 8 x 9 = 72. This method is more efficient than listing multiples, particularly when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b) = (|a * b|) / GCD(a, b)
where |a * b| represents the absolute value of the product of a and b.
- Finding the GCD of 18 and 8: We can use the Euclidean algorithm to find the GCD.
- 18 = 2 x 8 + 2
- 8 = 4 x 2 + 0
The last non-zero remainder is 2, so the GCD(18, 8) = 2.
- Applying the formula: LCM(18, 8) = (18 * 8) / 2 = 144 / 2 = 72
This method elegantly connects the concepts of LCM and GCD, offering another efficient way to calculate the LCM. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers.
Real-World Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine two buses leaving a terminal at different intervals. One bus leaves every 18 minutes, and another leaves every 8 minutes. The LCM (72 minutes) determines when both buses will depart simultaneously again. This principle is applicable to various scheduling problems, such as coordinating events or managing production cycles.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps in finding the least common denominator (LCD), making calculations easier and more efficient.
-
Cyclic Phenomena: LCM is relevant in situations involving periodic events like planetary orbits, wave patterns, or recurring natural phenomena. Finding the LCM can help predict when these events will coincide.
-
Modular Arithmetic: In cryptography and other areas of mathematics, LCM plays a crucial role in modular arithmetic, where operations are performed within a defined range of numbers.
-
Music Theory: The frequencies of musical notes are related to each other through ratios and LCM can be used to determine harmonious intervals between different notes.
Frequently Asked Questions (FAQ)
Q1: Is there only one LCM for two numbers?
A1: Yes, there is only one least common multiple for any pair of integers. While there are multiple common multiples, only one is the smallest.
Q2: What if one of the numbers is zero?
A2: The LCM of any number and zero is undefined. The concept of multiples doesn't apply to zero in this context.
Q3: Can I use a calculator to find the LCM?
A3: Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers.
Q4: Is there a difference between LCM and GCD?
A4: Yes, the LCM is the smallest common multiple, while the GCD is the largest common divisor. They are inversely related, as shown by the formula: LCM(a,b) = (|a*b|) / GCD(a,b).
Q5: How can I practice finding the LCM?
A5: Practice with various pairs of numbers using different methods. Start with small numbers and gradually increase the complexity. Online resources and textbooks offer many practice problems.
Conclusion
Finding the LCM of 18 and 8, which is 72, is a seemingly simple calculation, but understanding the methods and the underlying concepts opens the door to a deeper appreciation of number theory and its practical applications. Whether you use listing multiples, prime factorization, or the GCD method, the core principle remains the same: identifying the smallest positive integer that is divisible by both numbers. Mastering the calculation of LCM empowers you to tackle more complex mathematical problems and real-world scenarios involving cycles, scheduling, and fractions, highlighting the significance of this seemingly simple arithmetic operation. The journey to understanding LCM is not just about the answer but about the process and the broader mathematical connections it reveals.
Latest Posts
Latest Posts
-
1 6 Is Equal To
Sep 13, 2025
-
Gcf Of 12 And 40
Sep 13, 2025
-
Equivalent Fraction Of 3 6
Sep 13, 2025
-
0 25 Acres In Square Feet
Sep 13, 2025
-
6 5 As A Percentage
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 18 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.