2/9 -9/10 As A Fraction
saludintensiva
Sep 19, 2025 · 6 min read
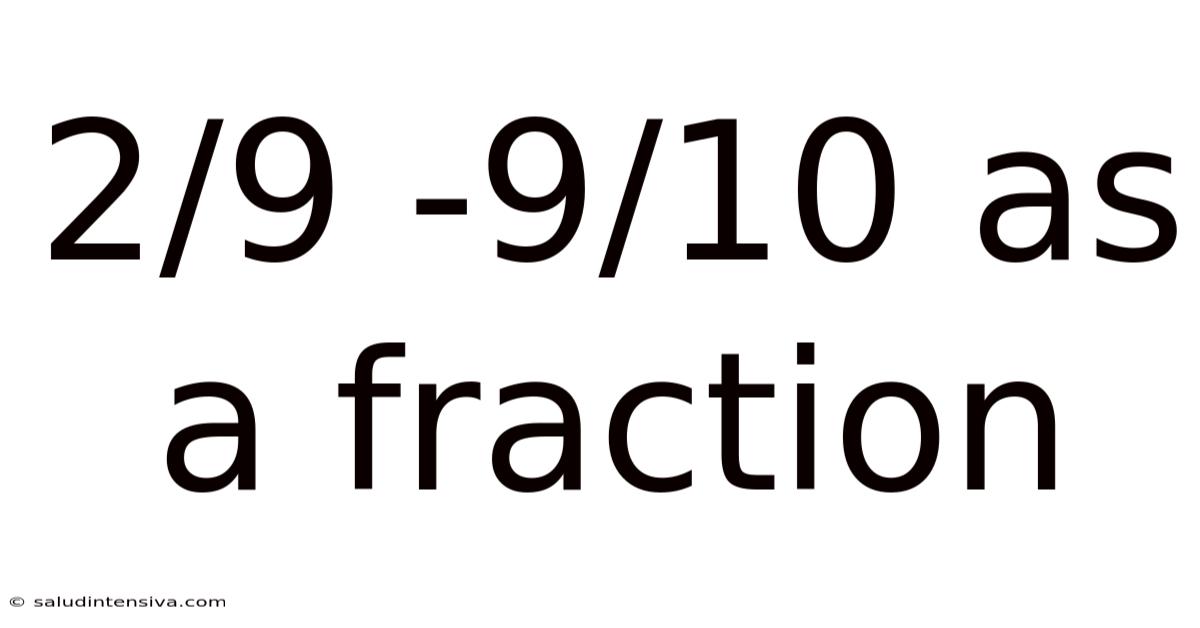
Table of Contents
Unveiling the Mystery: Understanding 2/9 - 9/10 as a Fraction
This article delves into the intricacies of subtracting fractions, specifically focusing on the seemingly complex problem of 2/9 - 9/10. We'll break down the process step-by-step, explaining the underlying mathematical principles in a clear and accessible way, suitable for learners of all levels. Understanding how to subtract fractions is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific concepts. We will not only solve this specific problem but also equip you with the knowledge to tackle similar fraction subtraction problems with confidence.
Introduction: A Primer on Fraction Subtraction
Before tackling the specific problem of 2/9 - 9/10, let's refresh our understanding of fraction subtraction. Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
Subtracting fractions involves finding the difference between two fractions. The fundamental rule is that you can only directly subtract fractions if they have the same denominator. If the denominators are different, we must find a common denominator before proceeding. This common denominator is usually the least common multiple (LCM) of the original denominators.
Finding the Least Common Multiple (LCM)
The LCM is the smallest number that is a multiple of both denominators. Finding the LCM is crucial for subtracting fractions with unlike denominators. Let's find the LCM of 9 and 10 for our problem:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
Notice that 90 is the smallest number present in both lists. Therefore, the LCM of 9 and 10 is 90.
Converting Fractions to a Common Denominator
Now that we have the LCM (90), we need to convert both fractions, 2/9 and 9/10, to equivalent fractions with a denominator of 90. To do this, we multiply both the numerator and the denominator of each fraction by the appropriate factor:
-
For 2/9: To get a denominator of 90, we multiply both the numerator and the denominator by 10 (since 9 x 10 = 90). This gives us (2 x 10) / (9 x 10) = 20/90.
-
For 9/10: To get a denominator of 90, we multiply both the numerator and the denominator by 9 (since 10 x 9 = 90). This gives us (9 x 9) / (10 x 9) = 81/90.
Performing the Subtraction
Now that both fractions have the same denominator (90), we can subtract them directly:
20/90 - 81/90 = (20 - 81) / 90 = -61/90
Therefore, the result of 2/9 - 9/10 is -61/90.
Understanding Negative Fractions
The result we obtained, -61/90, is a negative fraction. This simply means that the value of 9/10 is greater than the value of 2/9, resulting in a negative difference. Negative fractions represent values less than zero. They are handled in the same way as positive fractions, but the negative sign must be included in all calculations and representations.
Visual Representation: Understanding Fractions Geometrically
To further solidify understanding, let's visualize this subtraction. Imagine a circle divided into 90 equal parts. 2/9 represents 20 of these parts (as calculated earlier), while 9/10 represents 81 parts. Subtracting 81 parts from 20 parts leaves us with a deficit of 61 parts, hence the negative result. This visual representation helps to connect the abstract concept of fractions to a concrete geometrical model.
Step-by-Step Guide for Subtracting Fractions: A General Approach
Let's generalize the steps involved in subtracting fractions to handle any problem:
-
Find the Least Common Multiple (LCM) of the denominators: This is the key to converting the fractions to a common denominator. Methods for finding the LCM include listing multiples or using prime factorization.
-
Convert each fraction to an equivalent fraction with the LCM as the denominator: Multiply both the numerator and the denominator of each fraction by the appropriate factor to achieve the common denominator.
-
Subtract the numerators: Keep the common denominator the same.
-
Simplify the result (if possible): Reduce the resulting fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Frequently Asked Questions (FAQ)
-
Q: What if the fractions are mixed numbers?
- A: Convert the mixed numbers to improper fractions first. A mixed number (e.g., 1 2/3) is converted to an improper fraction by multiplying the whole number by the denominator and adding the numerator (1*3 + 2 = 5), then keeping the same denominator (5/3). After converting, follow the steps outlined above.
-
Q: Can I use a calculator to solve fraction subtraction problems?
- A: While calculators can perform the arithmetic, understanding the underlying principles is essential. Calculators can be a useful tool for checking your work, but they shouldn't replace the process of learning the method.
-
Q: Are there other methods to find the LCM?
- A: Yes, prime factorization is a powerful method to find the LCM. You break down each denominator into its prime factors, and then the LCM is found by taking the highest power of each prime factor present in either denominator. For example, for 9 (3²) and 10 (2 x 5), the LCM is 2 x 3² x 5 = 90.
-
Q: What if I get a fraction that can be simplified?
- A: Always simplify your final answer. Divide both the numerator and the denominator by their greatest common divisor (GCD) to express the fraction in its simplest form. For example, 12/18 simplifies to 2/3 because the GCD of 12 and 18 is 6.
Conclusion: Mastering Fraction Subtraction
Subtracting fractions, even seemingly complex ones like 2/9 - 9/10, becomes manageable with a systematic approach. By understanding the concepts of least common multiples, equivalent fractions, and the importance of a common denominator, you can confidently tackle any fraction subtraction problem. Remember the step-by-step guide and utilize the visual aids to enhance comprehension. Practice is key to mastering this fundamental mathematical skill. With consistent effort, you’ll develop a strong understanding of fractions and build a solid foundation for more advanced mathematical concepts. This article provides a comprehensive guide, aiming not only to solve the specific problem but also to equip you with the broader skill of fraction subtraction, enabling you to approach future challenges with increased confidence and understanding.
Latest Posts
Latest Posts
-
How Big 5000 Square Feet
Sep 19, 2025
-
12 45 As A Percentage
Sep 19, 2025
-
Simplify 1 I I 1
Sep 19, 2025
-
10 X 7 X 3
Sep 19, 2025
-
How To Off A Calculator
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2/9 -9/10 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.