2 Square Root Of 6
saludintensiva
Sep 24, 2025 · 5 min read
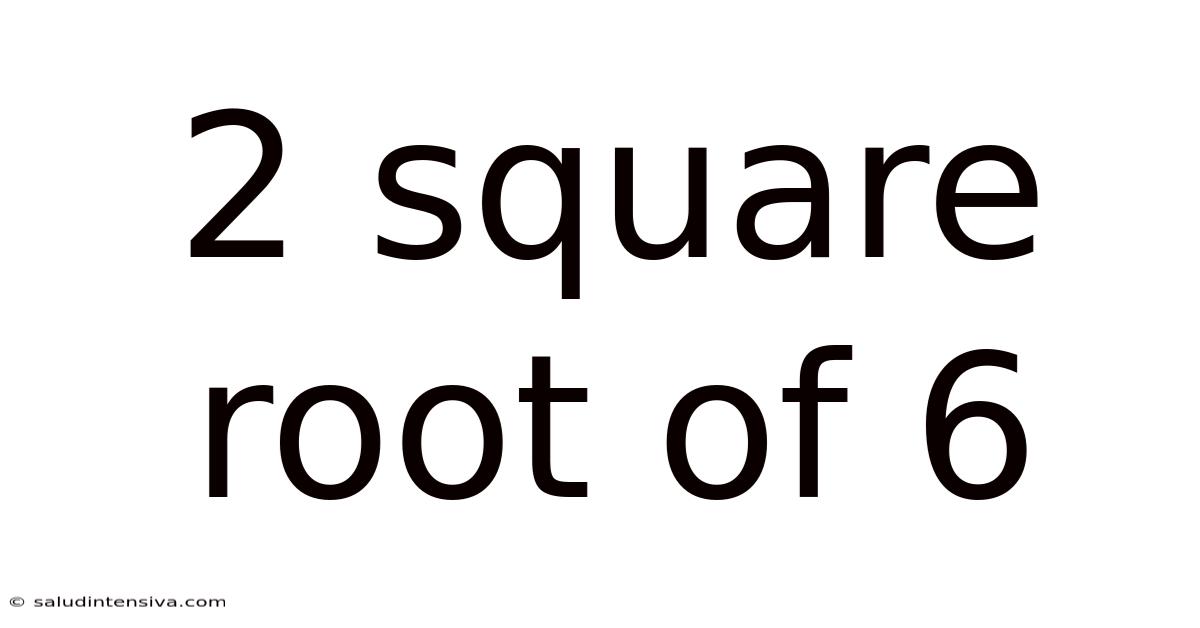
Table of Contents
Unveiling the Mysteries of 2√6: A Deep Dive into Irrational Numbers
Understanding the square root of a number is fundamental to mathematics, and 2√6, while seemingly simple, offers a rich opportunity to explore concepts like irrational numbers, simplification, approximations, and their applications in various fields. This comprehensive guide will delve into the intricacies of 2√6, demystifying its properties and exploring its significance within the broader mathematical landscape.
Introduction: What is 2√6?
The expression 2√6 represents twice the square root of 6. In simpler terms, it's the number that, when multiplied by itself, results in 24 (because (2√6)² = 4 * 6 = 24). This number is irrational, meaning it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, stretching infinitely without ever falling into a predictable pattern. This characteristic distinguishes it from rational numbers like 1/2 or 3/4, which can be expressed as finite decimals (0.5 and 0.75 respectively) or repeating decimals (1/3 = 0.333...). Understanding this fundamental difference is crucial to grasping the nature of 2√6. Throughout this article, we will explore methods for approximating its value, its significance in geometry, and its applications in more advanced mathematical concepts.
Understanding Square Roots and Irrational Numbers
Before we delve deeper into 2√6, let's revisit the concept of square roots. The square root of a number 'x' (denoted as √x) is a value that, when multiplied by itself, equals x. For example, √9 = 3 because 3 * 3 = 9. However, not all numbers have perfect square roots that are integers. For instance, √6 does not have a whole number solution. This is where irrational numbers come into play.
Irrational numbers are numbers that cannot be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. They are numbers with decimal representations that continue infinitely without repeating. Besides √6, other famous examples of irrational numbers include π (pi), approximately 3.14159..., and e (Euler's number), approximately 2.71828.... These numbers are fundamental in various branches of mathematics and science. 2√6 inherits the irrationality of √6, meaning it too has an infinite, non-repeating decimal representation.
Simplifying 2√6
While we can't simplify 2√6 into a rational number, we can check if the expression itself can be simplified. The number under the square root (the radicand) is 6. We look for perfect square factors of 6. Since 6 = 2 x 3, and neither 2 nor 3 are perfect squares, we cannot simplify √6 further. Therefore, 2√6 is already in its simplest radical form. This means the expression cannot be further reduced while maintaining its exact value.
Approximating the Value of 2√6
Since 2√6 is irrational, we cannot express its exact value as a decimal. However, we can approximate its value using various methods.
-
Using a Calculator: The simplest method is to use a calculator. Inputting "2√6" will give you an approximation, typically to several decimal places. This is a quick and convenient approach for everyday calculations.
-
Using Estimation: We know that √4 = 2 and √9 = 3. Since 6 lies between 4 and 9, √6 will lie between 2 and 3. A reasonable estimate might be around 2.4. Multiplying this by 2 gives us an approximation of 4.8 for 2√6. This method is useful for quick, rough estimations without access to a calculator.
-
Iterative Methods: More advanced methods, such as the Babylonian method (also known as Heron's method), can be used to iteratively refine the approximation of √6 and then multiply by 2. This method provides progressively more accurate approximations with each iteration.
Geometric Interpretation of 2√6
The number 2√6 has a concrete geometric interpretation. Consider a right-angled triangle with legs of length 2 and √6. Using the Pythagorean theorem (a² + b² = c²), the hypotenuse (c) of this triangle would have a length of √(2² + (√6)²) = √(4 + 6) = √10. Similarly, we can construct other geometric figures where 2√6 plays a role in determining lengths or areas. This connection between numbers and geometric shapes highlights the deep relationship between algebra and geometry.
Applications of 2√6 and Irrational Numbers
Irrational numbers, including 2√6, appear frequently in various fields:
-
Physics: Many physical constants and calculations involve irrational numbers. For example, the calculation of projectile motion, oscillations, and wave phenomena often leads to expressions involving irrational numbers.
-
Engineering: Engineering designs often require precise calculations, and irrational numbers are unavoidable in many geometric and structural calculations.
-
Computer Science: Representing irrational numbers in computer systems poses challenges due to their infinite decimal representation. Algorithms and techniques are needed to handle these numbers with a degree of accuracy depending on the application's requirements.
-
Financial Modeling: In certain financial models, irrational numbers might appear in calculations related to interest rates, compound growth, and probability distributions.
Frequently Asked Questions (FAQ)
-
Q: Is 2√6 a rational or irrational number?
- A: 2√6 is an irrational number. It cannot be expressed as a fraction of two integers.
-
Q: How can I simplify 2√6?
- A: 2√6 is already in its simplest form. The number 6 does not have any perfect square factors other than 1.
-
Q: What is the approximate value of 2√6?
- A: The approximate value of 2√6 is approximately 4.898979. This can be obtained using a calculator or through iterative methods.
-
Q: What are some real-world applications of irrational numbers?
- A: Irrational numbers appear in various fields, including physics (calculations involving π in circles and spheres), engineering (geometric calculations), and computer graphics (representing curves and shapes).
-
Q: Can 2√6 be expressed as a decimal?
- A: Yes, but it will be a non-terminating, non-repeating decimal. We can only approximate its value as a decimal.
Conclusion: The Significance of 2√6
While seemingly a simple mathematical expression, 2√6 serves as a potent example of an irrational number, highlighting the richness and complexity inherent in seemingly simple mathematical concepts. Understanding its properties, its approximations, and its geometric interpretation allows for a deeper appreciation of the intricacies of mathematics and its broad applications across various scientific and engineering fields. The exploration of 2√6 provides a stepping stone for further exploration of more complex mathematical ideas and their practical implications in the real world. Its inherent irrationality underscores the boundless nature of mathematical discovery and the beauty found in numbers that stretch beyond finite representation.
Latest Posts
Latest Posts
-
63 Acres To Sq Ft
Sep 24, 2025
-
60 Days From Nov 1
Sep 24, 2025
-
4 30 As A Percent
Sep 24, 2025
-
Negative 3 Minus Negative 6
Sep 24, 2025
-
6 2 1 2 Pemdas
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.