23/5 As A Mixed Number
saludintensiva
Sep 10, 2025 · 6 min read
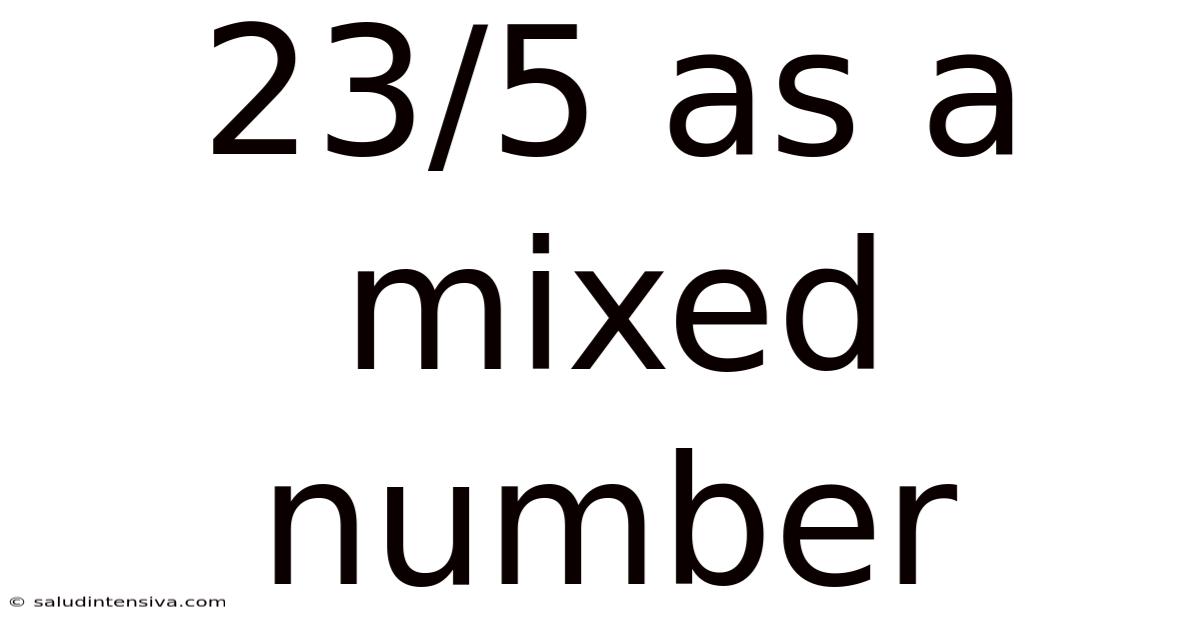
Table of Contents
Understanding 23/5 as a Mixed Number: A Comprehensive Guide
The concept of mixed numbers is fundamental in mathematics, bridging the gap between whole numbers and fractions. This article will delve deep into understanding how to represent the improper fraction 23/5 as a mixed number, explaining the process thoroughly and exploring related concepts. We'll cover the steps involved, the underlying mathematical principles, and answer frequently asked questions to solidify your understanding. This guide is perfect for students learning about fractions or anyone seeking a refresher on this essential mathematical skill.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number), like 1/2, 3/4, or 2/5. Mixed numbers are useful for representing quantities that are greater than one but not a whole number. For instance, 1 1/2 represents one whole unit and half of another. Improper fractions, on the other hand, have a numerator that is greater than or equal to the denominator, like 7/4 or 23/5. Converting improper fractions to mixed numbers makes it easier to visualize and understand the quantity.
Converting 23/5 to a Mixed Number: A Step-by-Step Guide
To convert the improper fraction 23/5 into a mixed number, we follow these simple steps:
-
Divide the numerator by the denominator: We divide 23 (the numerator) by 5 (the denominator).
23 ÷ 5 = 4 with a remainder of 3
-
Identify the whole number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 4.
-
Identify the new numerator: The remainder from the division becomes the numerator of the fraction part of the mixed number. Our remainder is 3.
-
Keep the original denominator: The denominator of the fraction in the mixed number remains the same as the denominator of the original improper fraction. Therefore, the denominator remains 5.
-
Combine the whole number and the fraction: We combine the whole number from step 2 and the fraction from steps 3 and 4 to create the mixed number.
Therefore, 23/5 as a mixed number is 4 3/5.
Visualizing the Conversion
Imagine you have 23 identical items, and you want to group them into sets of 5. You can form 4 complete sets of 5 (4 x 5 = 20), leaving 3 items remaining (23 - 20 = 3). This visually represents the mixed number 4 3/5. You have 4 complete sets and 3/5 of another set.
The Mathematical Principle Behind the Conversion
The process of converting an improper fraction to a mixed number is essentially the same as performing division with a remainder. We're dividing the quantity represented by the numerator into equal parts determined by the denominator. The quotient represents the number of complete groups, while the remainder represents the portion of a group that's left over. This is a fundamental concept linked to Euclidean division, a cornerstone of number theory.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. Let's use our example, 4 3/5:
-
Multiply the whole number by the denominator: 4 (whole number) x 5 (denominator) = 20
-
Add the numerator: Add the result from step 1 to the numerator of the fraction: 20 + 3 (numerator) = 23
-
Keep the denominator: The denominator remains the same: 5
-
Form the improper fraction: Combine the result from step 2 as the numerator and the denominator from step 3 to form the improper fraction: 23/5
This demonstrates the equivalence between the improper fraction 23/5 and the mixed number 4 3/5.
Applications of Mixed Numbers
Mixed numbers are frequently encountered in various real-world applications:
-
Measurement: Expressing measurements like length (e.g., 2 1/2 inches), weight (e.g., 1 3/4 pounds), or volume (e.g., 3 1/2 liters).
-
Cooking and Baking: Following recipes often involves using mixed numbers to specify ingredient quantities (e.g., 1 1/2 cups of flour).
-
Time: Representing durations that are not whole hours (e.g., 2 1/2 hours).
-
Construction and Engineering: Calculations involving dimensions and quantities often require the use of mixed numbers for precise measurements.
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires a bit more care than working solely with improper fractions or whole numbers. The key is to either convert the mixed numbers to improper fractions first, then perform the addition or subtraction, or to add/subtract the whole numbers and fractional parts separately. Let’s illustrate with an example:
Example: Add 2 1/3 and 1 2/3
Method 1: Converting to Improper Fractions
- 2 1/3 = (2 x 3 + 1)/3 = 7/3
- 1 2/3 = (1 x 3 + 2)/3 = 5/3
- 7/3 + 5/3 = 12/3 = 4
Method 2: Adding Whole and Fractional Parts Separately
- Add the whole numbers: 2 + 1 = 3
- Add the fractions: 1/3 + 2/3 = 3/3 = 1
- Combine the results: 3 + 1 = 4
Working with Mixed Numbers: Multiplication and Division
Multiplying and dividing mixed numbers also benefit from first converting them into improper fractions. This simplifies the calculations. Let's demonstrate multiplication:
Example: Multiply 2 1/2 by 3 1/3
- 2 1/2 = (2 x 2 + 1)/2 = 5/2
- 3 1/3 = (3 x 3 + 1)/3 = 10/3
- (5/2) x (10/3) = 50/6 = 25/3 = 8 1/3
Frequently Asked Questions (FAQs)
Q1: Why do we use mixed numbers?
A1: Mixed numbers provide a more intuitive and easily understandable representation of quantities that are greater than one but not whole numbers. They make calculations involving fractions less abstract.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, every improper fraction can be converted to a mixed number or a whole number.
Q3: What if the remainder is zero when converting an improper fraction to a mixed number?
A3: If the remainder is zero, it means the improper fraction is equivalent to a whole number. For example, 10/5 would be 2.
Q4: Are there any situations where improper fractions are preferred over mixed numbers?
A4: In some mathematical operations, such as multiplication and division, using improper fractions can simplify the calculations.
Conclusion
Understanding how to convert improper fractions to mixed numbers and vice versa is a critical skill in mathematics. This process is grounded in the fundamental principles of division and provides a powerful tool for working with fractional quantities in various real-world applications. This article has aimed to provide a comprehensive understanding of this concept, equipping you with the knowledge to confidently work with mixed numbers and navigate related mathematical problems. Remember to practice regularly to solidify your understanding and build proficiency with this essential skill. By mastering the conversion between improper fractions and mixed numbers, you'll enhance your overall mathematical capabilities and gain greater confidence in tackling more complex problems.
Latest Posts
Latest Posts
-
How To Multiply Divide Fractions
Sep 10, 2025
-
20 Percent As A Decimal
Sep 10, 2025
-
Estimating Sums And Differences Fractions
Sep 10, 2025
-
90 Days From 7 10
Sep 10, 2025
-
8 20 As A Decimal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 23/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.