8 20 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
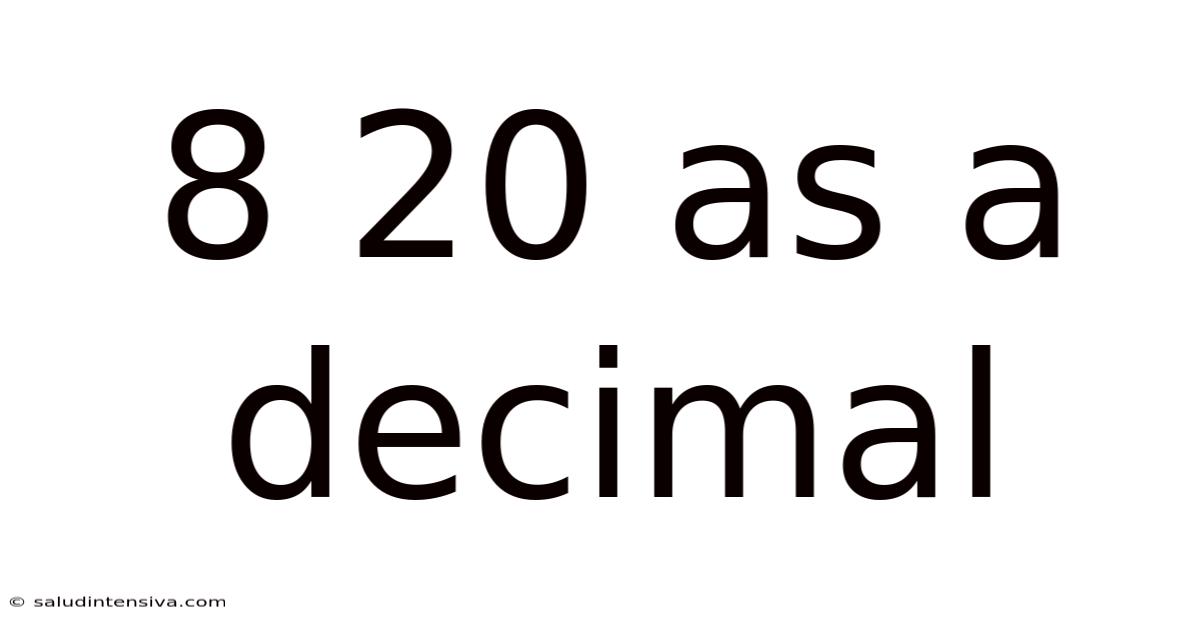
Table of Contents
Understanding 8/20 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the fraction 8/20 to its decimal equivalent, explaining the underlying principles and providing practical examples. We'll delve into different methods, address common misconceptions, and explore related concepts to solidify your understanding. This guide aims to provide a clear, step-by-step approach that's accessible to learners of all levels.
Introduction: Decimals and Fractions
Before diving into the conversion of 8/20, let's briefly review the concepts of decimals and fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is another way to represent a part of a whole, using the base-10 number system. Decimals use a decimal point to separate the whole number part from the fractional part. For instance, 0.5 represents one-half (1/2). The key is understanding that fractions and decimals are simply different ways of expressing the same numerical value.
Method 1: Simplifying the Fraction
The simplest and often most efficient method for converting a fraction to a decimal involves simplifying the fraction before performing the division. This is particularly useful when dealing with larger numbers.
Step 1: Find the Greatest Common Divisor (GCD)
The first step is to find the greatest common divisor (GCD) of the numerator (8) and the denominator (20). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 8 and 20 is 4.
Step 2: Simplify the Fraction
Divide both the numerator and the denominator by the GCD:
8 ÷ 4 = 2 20 ÷ 4 = 5
This simplifies the fraction 8/20 to 2/5.
Step 3: Perform the Division
Now, divide the simplified numerator (2) by the simplified denominator (5):
2 ÷ 5 = 0.4
Therefore, 8/20 is equal to 0.4 as a decimal.
Method 2: Direct Division
Alternatively, you can directly divide the numerator by the denominator without simplifying the fraction beforehand. This method is straightforward but can be more time-consuming if the numbers are large.
Step 1: Set up the Division
Write the division problem as 8 ÷ 20.
Step 2: Perform the Long Division
Perform the long division. Since 8 is smaller than 20, you'll need to add a decimal point and a zero to the dividend (8) to continue the division.
0.4
20 | 8.0
8.0
---
0
The result of the division is 0.4. Therefore, 8/20 equals 0.4.
Method 3: Using a Calculator
The most straightforward method, especially for complex fractions, is to use a calculator. Simply enter the fraction as 8/20 and press the equals sign (=). The calculator will directly provide the decimal equivalent, which is 0.4. While convenient, understanding the underlying mathematical processes remains essential for building a strong foundation in mathematics.
Understanding the Decimal Value: Place Value
The decimal 0.4 represents four-tenths. Understanding place value is crucial. The digit immediately to the right of the decimal point represents the tenths place, the next digit represents the hundredths place, and so on. In 0.4, the 4 is in the tenths place, meaning it represents 4/10.
This reinforces the equivalence between the fraction 2/5 and the decimal 0.4. Both represent the same numerical value: four-tenths or two-fifths of a whole.
Further Exploration: Percentages
The decimal 0.4 can also easily be converted to a percentage. To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%).
0.4 x 100 = 40%
Therefore, 8/20 is equivalent to 40%. This highlights the interconnectedness of fractions, decimals, and percentages, all different ways of expressing proportions.
Common Misconceptions
A common misconception is that simplifying a fraction is optional when converting to a decimal. While you can perform the division directly, simplifying often makes the calculation easier and less prone to errors, particularly with larger numbers. Always aim for efficiency and accuracy.
Practical Applications
Converting fractions to decimals is essential in numerous real-world applications:
- Financial calculations: Calculating percentages, discounts, interest rates, and profit margins often involves converting fractions to decimals.
- Scientific measurements: Many scientific measurements are expressed in decimal form, requiring conversion from fractional representations.
- Engineering and construction: Precise measurements and calculations are vital in these fields, demanding proficiency in decimal conversions.
- Everyday calculations: Dividing quantities, sharing items, or determining proportions frequently involve converting fractions to decimals for easier computation.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a decimal?
A1: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. However, some fractions will result in repeating decimals (e.g., 1/3 = 0.333...).
Q2: What if the decimal conversion is a repeating decimal?
A2: Repeating decimals are perfectly valid and represent a rational number (a number that can be expressed as a fraction). They are often represented using a bar over the repeating digits (e.g., 0.333... is written as 0.3̅).
Q3: Is there a difference between simplifying a fraction before or after converting it to a decimal?
A3: No, the final decimal value will be the same whether you simplify the fraction before or after performing the division. Simplifying beforehand makes the calculation simpler and less error-prone.
Q4: How can I improve my skills in converting fractions to decimals?
A4: Practice is key! Work through numerous examples, starting with simple fractions and gradually increasing the complexity. Use different methods to build your understanding and choose the approach most comfortable for you. Pay close attention to place value in decimal numbers.
Conclusion: Mastering Decimal Conversions
Converting the fraction 8/20 to its decimal equivalent (0.4) is a straightforward process, easily accomplished through simplification and division. Understanding the underlying principles of fractions, decimals, and place value is crucial for mastering this fundamental mathematical skill. This skill is widely applicable in various contexts, from everyday calculations to complex scientific and engineering tasks. Regular practice and a clear understanding of the methods described above will ensure proficiency in converting fractions to decimals and effectively utilizing this skill in a variety of situations. Remember, the key to success lies in consistent practice and a solid grasp of the underlying mathematical concepts.
Latest Posts
Latest Posts
-
5 To The 4th Power
Sep 10, 2025
-
1 15 Random Number Generator
Sep 10, 2025
-
Lcm For 8 And 3
Sep 10, 2025
-
3 5 As A Mixed Number
Sep 10, 2025
-
What Is Equivalent To 10 12
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 8 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.