23 50 As A Decimal
saludintensiva
Sep 17, 2025 · 5 min read
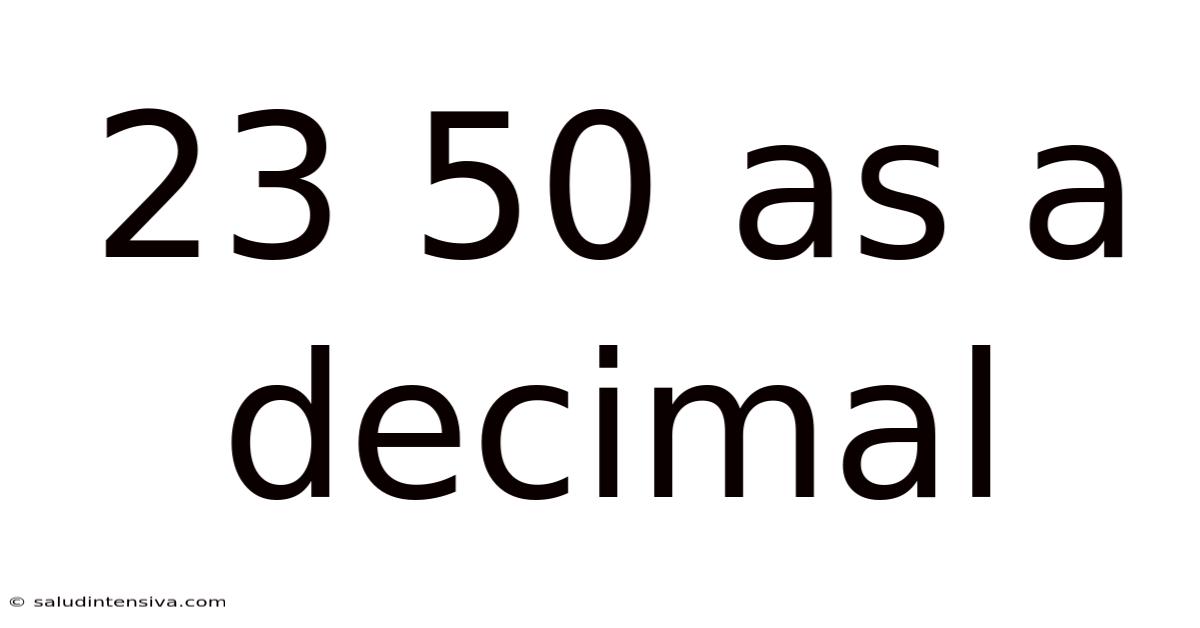
Table of Contents
23/50 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide delves into the conversion of the fraction 23/50 to its decimal equivalent, explaining the process step-by-step and exploring the underlying principles. We'll also examine related concepts and answer frequently asked questions to provide a complete understanding of this mathematical operation.
Introduction: Fractions and Decimals
Fractions and decimals are two different ways of representing parts of a whole. A fraction expresses a part as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, expresses a part using a base-ten system, with a decimal point separating the whole number part from the fractional part. Converting between fractions and decimals is often necessary for comparisons, calculations, and problem-solving.
The fraction 23/50 represents 23 parts out of a total of 50 parts. Our goal is to express this same quantity as a decimal number.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. We divide the numerator (23) by the denominator (50):
23 ÷ 50 = 0.46
Therefore, 23/50 as a decimal is 0.46.
This method is simple and readily applicable using a calculator or long division. Long division involves the following steps:
- Set up the division: Write 23 as the dividend (inside the division symbol) and 50 as the divisor (outside the division symbol).
- Add a decimal point and zeros: Add a decimal point to the right of 23 and add zeros as needed. Since 50 doesn't go into 23, we add a decimal point and continue dividing.
- Perform the division: Divide 230 by 50. 50 goes into 230 four times (50 x 4 = 200). Subtract 200 from 230, leaving a remainder of 30.
- Bring down zeros: Bring down a zero from the dividend, making it 300. Divide 300 by 50; this is 6 (50 x 6 = 300). There's no remainder.
- Write the decimal: The result is 0.46.
Method 2: Equivalent Fractions and Decimal Equivalents
Another approach involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This method is particularly useful when the denominator has factors that easily simplify to powers of 10.
In this case, we can multiply both the numerator and the denominator of 23/50 by 2:
(23 x 2) / (50 x 2) = 46/100
Since 100 is 10², we can easily express 46/100 as a decimal. Remember that the denominator represents the number of decimal places; 100 has two zeros, so the decimal will have two decimal places. Therefore:
46/100 = 0.46
This method demonstrates the relationship between fractions and decimals, highlighting how changing the denominator affects the decimal representation.
Understanding Decimal Place Value
The decimal system uses place value to represent the magnitude of each digit. In the decimal 0.46:
- 0: Represents the whole number part (in this case, zero whole units).
- 4: Represents four-tenths (4/10).
- 6: Represents six-hundredths (6/100).
Therefore, 0.46 is the sum of 4/10 and 6/100, which equals 46/100, equivalent to 23/50.
Applications of Decimal Conversions
The ability to convert fractions to decimals is crucial in various contexts:
- Financial Calculations: Calculating percentages, interest rates, and discounts often requires converting fractions to decimals.
- Scientific Measurements: Many scientific measurements are expressed in decimal form.
- Data Analysis: When working with data sets, converting fractions to decimals facilitates statistical analysis and comparisons.
- Engineering and Design: Precise measurements and calculations are vital in engineering and design, and decimals are frequently used.
Further Exploration: Repeating Decimals
While 23/50 converts to a terminating decimal (a decimal that ends), not all fractions do. Some fractions produce repeating decimals, which have a sequence of digits that repeat infinitely. For example, 1/3 equals 0.3333... (the 3 repeats indefinitely). Understanding the difference between terminating and repeating decimals is essential for accurate calculations.
Frequently Asked Questions (FAQ)
Q1: How do I convert any fraction to a decimal?
A: The primary method is to divide the numerator by the denominator. You can use a calculator or perform long division. Alternatively, try to find an equivalent fraction with a denominator that is a power of 10.
Q2: What if the decimal representation goes on forever?
A: Some fractions produce repeating decimals. In such cases, you can either round the decimal to a specific number of decimal places or use a bar notation to indicate the repeating sequence. For example, 1/3 is represented as 0.3̅, with the bar indicating that the 3 repeats infinitely.
Q3: Can I convert decimals back to fractions?
A: Yes, absolutely! The process involves writing the decimal as a fraction with a denominator that is a power of 10 (depending on the number of decimal places) and then simplifying the fraction if possible. For example, 0.46 can be written as 46/100, which simplifies to 23/50.
Q4: Are there any online tools to help with fraction-to-decimal conversions?
A: Yes, many online calculators and converters are available that can quickly perform fraction-to-decimal conversions.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill with wide-ranging applications. The process, whether through direct division or by finding equivalent fractions, is relatively straightforward and easily mastered with practice. Understanding decimal place value and the possibility of repeating decimals completes the picture. By mastering this skill, you'll enhance your mathematical proficiency and confidently tackle numerical problems across various fields. Remember that consistent practice is key to developing fluency in this crucial mathematical operation. The conversion of 23/50 to 0.46 is just one example illustrating a broader principle – a principle that underpins many calculations and applications in mathematics and beyond.
Latest Posts
Latest Posts
-
1 9 16 To Decimal
Sep 17, 2025
-
27 To The Power Of
Sep 17, 2025
-
Whats Equivalent To 1 4
Sep 17, 2025
-
23 6 As A Mixed Number
Sep 17, 2025
-
7 8 As A Percentage
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 23 50 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.