7 8 As A Percentage
saludintensiva
Sep 17, 2025 · 5 min read
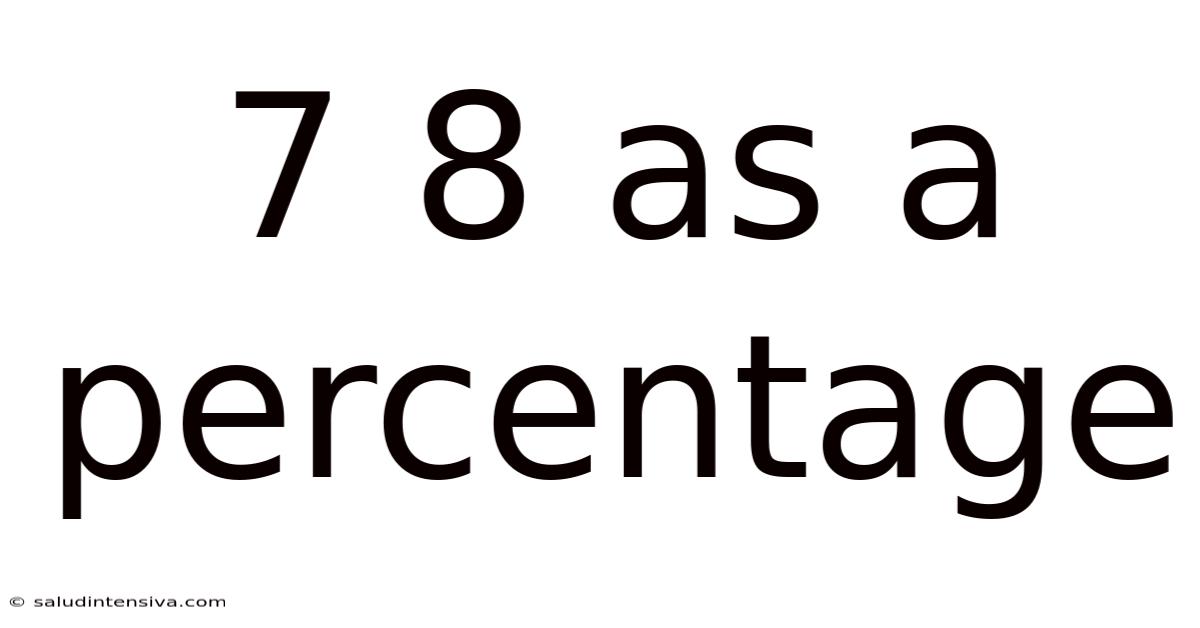
Table of Contents
Decoding 7/8 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article will comprehensively explore how to convert the fraction 7/8 into a percentage, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also cover common applications and answer frequently asked questions to ensure a thorough understanding of this essential concept.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specifics of converting 7/8 to a percentage, let's establish the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole. A fraction expresses a part of a whole as a ratio of two numbers (numerator and denominator). A decimal represents a part of a whole using base-10 notation. A percentage expresses a part of a whole as a fraction of 100. These three representations are interchangeable; you can convert one form into another without losing the original value.
Method 1: The Direct Conversion Method (Division and Multiplication)
This is the most straightforward method for converting a fraction to a percentage. It involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (7) by the denominator (8). 7 ÷ 8 = 0.875
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add a percentage sign (%). 0.875 × 100 = 87.5%
Therefore, 7/8 is equal to 87.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method relies on the understanding that a percentage is a fraction out of 100. To convert 7/8 to a percentage using this method, we need to find an equivalent fraction where the denominator is 100. This involves finding a number that, when multiplied by 8, results in 100. Unfortunately, this is not possible using whole numbers, since 100 is not divisible by 8. However, we can still use this principle to understand the concept. If we were dealing with a fraction that could be easily converted to a denominator of 100 (e.g., 25/50), we would simply simplify the fraction and express it as a percentage. This method is more useful for fractions where the denominator is a factor of 100 (e.g., 25, 50, 100).
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where one ratio is the given fraction (7/8) and the other is the unknown percentage (x/100). We then solve for x:
7/8 = x/100
Cross-multiply:
8x = 700
Solve for x:
x = 700/8 = 87.5
Therefore, x = 87.5%, confirming our previous results. This method provides a more algebraic approach to the conversion.
Understanding the Result: What Does 87.5% Mean?
87.5% means that 7 out of 8 parts represent 87.5% of the whole. Imagine a pizza cut into 8 equal slices. If you eat 7 slices, you have consumed 87.5% of the pizza. This percentage representation provides a clear and concise way to express the proportion of the whole that 7/8 represents.
Practical Applications of Percentage Conversions
Converting fractions to percentages has numerous real-world applications across various fields:
- Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns.
- Retail: Determining sale prices, calculating markups, and analyzing sales data.
- Science: Expressing experimental results, analyzing data, and calculating statistical probabilities.
- Education: Assessing student performance, analyzing test scores, and calculating grades.
- Everyday Life: Calculating tips, splitting bills, understanding unit pricing, and more.
Real-World Examples:
- Sales Discount: A store offers a 12.5% discount on an item. This is equivalent to 1/8 off. If the original price is $80, the discount is (1/8) * $80 = $10.
- Survey Results: In a survey of 800 people, 700 responded positively. The percentage of positive responses is (700/800) * 100 = 87.5%.
- Test Scores: A student answers 7 out of 8 questions correctly on a quiz. Their score is 87.5%.
Frequently Asked Questions (FAQ)
-
Q: Why do we multiply by 100 when converting a decimal to a percentage?
- A: A percentage is defined as a fraction out of 100. Multiplying by 100 scales the decimal value to express it as a fraction of 100.
-
Q: Can all fractions be easily converted to percentages with whole number percentages?
- A: No, some fractions will result in decimal percentages (like 87.5% in this case).
-
Q: What if the fraction is an improper fraction (numerator > denominator)?
- A: You still follow the same steps. Convert the improper fraction to a mixed number or decimal first, then convert the resulting decimal to a percentage. For example, 9/8 = 1.125 = 112.5%
-
Q: Are there any online calculators to help with these conversions?
- A: Yes, many online calculators are available to perform fraction-to-percentage conversions quickly and accurately. However, understanding the underlying mathematical process is crucial for applying this knowledge effectively.
-
Q: How can I improve my understanding of fractions and percentages?
- A: Practice is key! Work through various examples, solve problems, and use different methods to convert fractions and percentages. You can find plenty of practice exercises online and in textbooks.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting a fraction like 7/8 to a percentage is a fundamental mathematical skill with far-reaching implications. Through understanding the different conversion methods – direct conversion, equivalent fractions, and proportions – you gain a versatile tool for tackling various real-world problems involving proportions and ratios. By practicing these methods and exploring their applications, you can build a strong foundation in mathematical concepts and enhance your problem-solving abilities. Remember that the core concept is understanding the relationship between fractions, decimals, and percentages as interchangeable representations of parts of a whole. This knowledge empowers you to confidently navigate numerical challenges in various contexts, from everyday calculations to complex analytical tasks.
Latest Posts
Latest Posts
-
What Is 6 9 Equal To
Sep 17, 2025
-
15 Miles How Many Minutes
Sep 17, 2025
-
Is 6 8 Greater Than 3 4
Sep 17, 2025
-
1 3 2 2 3
Sep 17, 2025
-
16 3 As A Decimal
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 7 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.