3 10 As A Percent
saludintensiva
Sep 18, 2025 · 5 min read
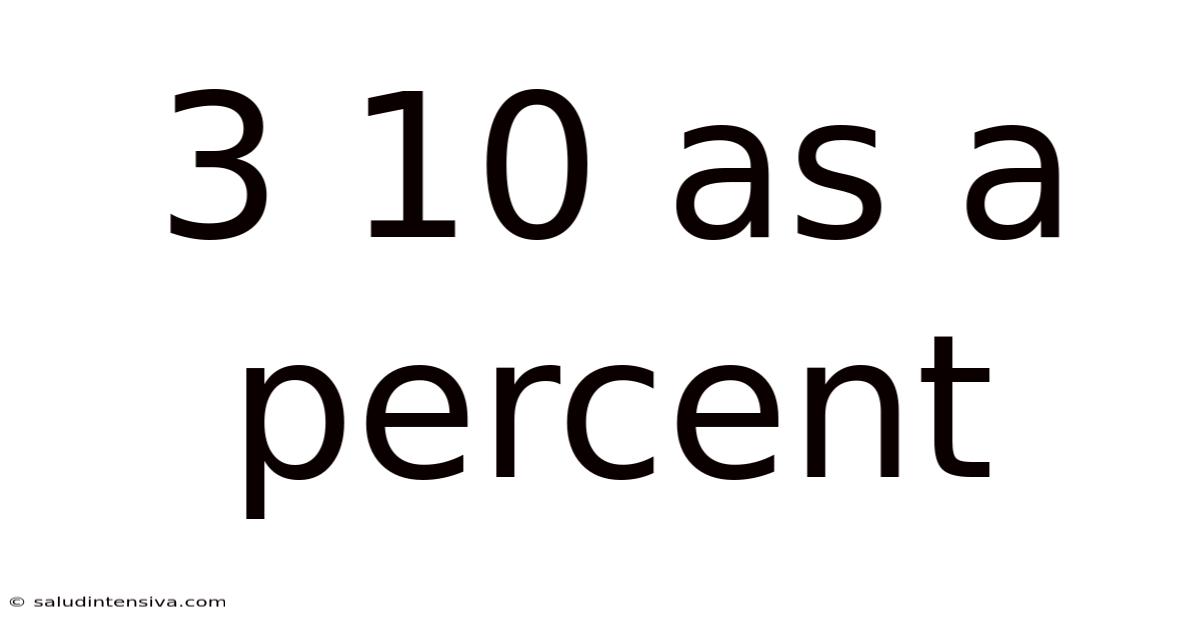
Table of Contents
3/10 as a Percent: A Comprehensive Guide to Understanding Fractions and Percentages
Understanding fractions and percentages is a fundamental skill in mathematics, crucial for everyday life, from calculating discounts to understanding financial reports. This article provides a comprehensive guide to converting fractions to percentages, focusing specifically on how to express 3/10 as a percent. We'll cover the underlying concepts, practical applications, and even delve into some advanced aspects to solidify your understanding. By the end, you'll not only know that 3/10 is 30%, but you'll also grasp the broader principles involved.
Understanding Fractions and Percentages
Before we tackle 3/10 specifically, let's review the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator. This means we have 3 parts out of a total of 10 parts.
A percentage is a way of expressing a fraction as a portion of 100. The word "percent" literally means "out of 100" (from the Latin "per centum"). Percentages are often used because they provide a standardized and easily comparable way to represent proportions. For instance, saying something is 30% is clearer and more intuitive than saying it's 3/10 for many people.
Converting 3/10 to a Percentage: The Step-by-Step Process
Converting a fraction to a percentage involves a straightforward two-step process:
Step 1: Convert the fraction to a decimal.
To do this, divide the numerator by the denominator. In our case:
3 ÷ 10 = 0.3
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.3 x 100 = 30
Therefore, 0.3 is equal to 30%.
Thus, 3/10 as a percent is 30%.
Visualizing 3/10 as 30%
Imagine a pizza cut into 10 equal slices. If you eat 3 slices, you've eaten 3 out of 10 slices, which is 3/10 of the pizza. This is equivalent to 30% of the pizza. Visual representations like this can greatly improve understanding, especially for beginners.
Real-World Applications of 3/10 (30%)
The concept of 3/10 or 30% appears in numerous real-world scenarios:
-
Sales and Discounts: A store might offer a 30% discount on an item. This means you'll pay only 70% of the original price (100% - 30% = 70%).
-
Statistics and Probability: In surveys or polls, 30% might represent the proportion of respondents who chose a particular option.
-
Financial Calculations: Interest rates, investment returns, and tax calculations often involve percentages, including instances where 30% plays a significant role.
-
Grades and Assessments: A score of 30% on a test indicates a poor performance, suggesting a need for improvement.
-
Data Representation: Charts and graphs frequently use percentages to illustrate proportions and trends. A bar chart might show that 30% of a company's revenue comes from a specific product line.
Further Exploration: Working with Different Fractions and Percentages
While we've focused on 3/10, the process of converting fractions to percentages remains the same for other fractions. Let's explore some examples:
-
1/4 as a percentage:
1 ÷ 4 = 0.25 0.25 x 100 = 25%
-
2/5 as a percentage:
2 ÷ 5 = 0.4 0.4 x 100 = 40%
-
7/8 as a percentage:
7 ÷ 8 = 0.875 0.875 x 100 = 87.5%
These examples illustrate the versatility of the conversion process. No matter the fraction, the fundamental steps remain consistent.
Advanced Concepts: Understanding Percentage Increase and Decrease
Beyond simple conversion, percentages are often used to represent changes in quantities. Consider these scenarios:
-
Percentage Increase: Suppose a company's profits increased from $100,000 to $130,000. The increase is $30,000. To find the percentage increase, divide the increase by the original amount and multiply by 100:
($30,000 / $100,000) x 100 = 30%
-
Percentage Decrease: If the company's profits decreased from $100,000 to $70,000, the decrease is $30,000. The percentage decrease is:
($30,000 / $100,000) x 100 = 30%
These calculations are essential for analyzing trends and making informed decisions.
Working with Percentages and Decimals: A Deeper Dive
Understanding the relationship between percentages, decimals, and fractions is key. Remember:
-
Percentage to Decimal: Divide the percentage by 100. For example, 30% = 30/100 = 0.3
-
Decimal to Percentage: Multiply the decimal by 100. For example, 0.75 = 0.75 x 100 = 75%
-
Fraction to Decimal: Divide the numerator by the denominator. For example, 3/10 = 3 ÷ 10 = 0.3
-
Decimal to Fraction: Write the decimal as a fraction over a power of 10. For example, 0.3 = 3/10
Mastering these conversions allows for seamless transitions between these different forms of representing proportions.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to convert a fraction to a percentage?
A: The easiest method is to first divide the numerator by the denominator to obtain a decimal, then multiply the decimal by 100 and add the "%" sign.
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the method described above.
Q: What if the fraction results in a repeating decimal when converted to a percentage?
A: If you encounter a repeating decimal, you can round it to a reasonable number of decimal places for practical purposes.
Q: Are there any shortcuts for converting fractions to percentages?
A: For some common fractions (like 1/2, 1/4, 1/5), you might memorize their percentage equivalents to speed up the process. However, the general method remains the most reliable for all fractions.
Conclusion
Converting 3/10 to a percentage is a simple yet fundamental mathematical operation. Understanding this conversion, along with the broader concepts of fractions and percentages, is crucial for navigating various aspects of life. This guide has provided a comprehensive explanation, illustrated with examples and real-world applications. By mastering these concepts, you'll enhance your numeracy skills and confidently tackle percentage-related problems in your personal and professional life. Remember that practice is key to solidifying your understanding. Work through various examples, and you'll soon find yourself comfortable converting fractions to percentages and vice versa.
Latest Posts
Latest Posts
-
175 Cm To Ft In
Sep 18, 2025
-
Is 2 3 More Than 3 4
Sep 18, 2025
-
18 Out Of 25 Percentage
Sep 18, 2025
-
7 6 As A Mixed Number
Sep 18, 2025
-
Convert 0 5 To A Fraction
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.