3/6 On A Number Line
saludintensiva
Sep 20, 2025 · 6 min read
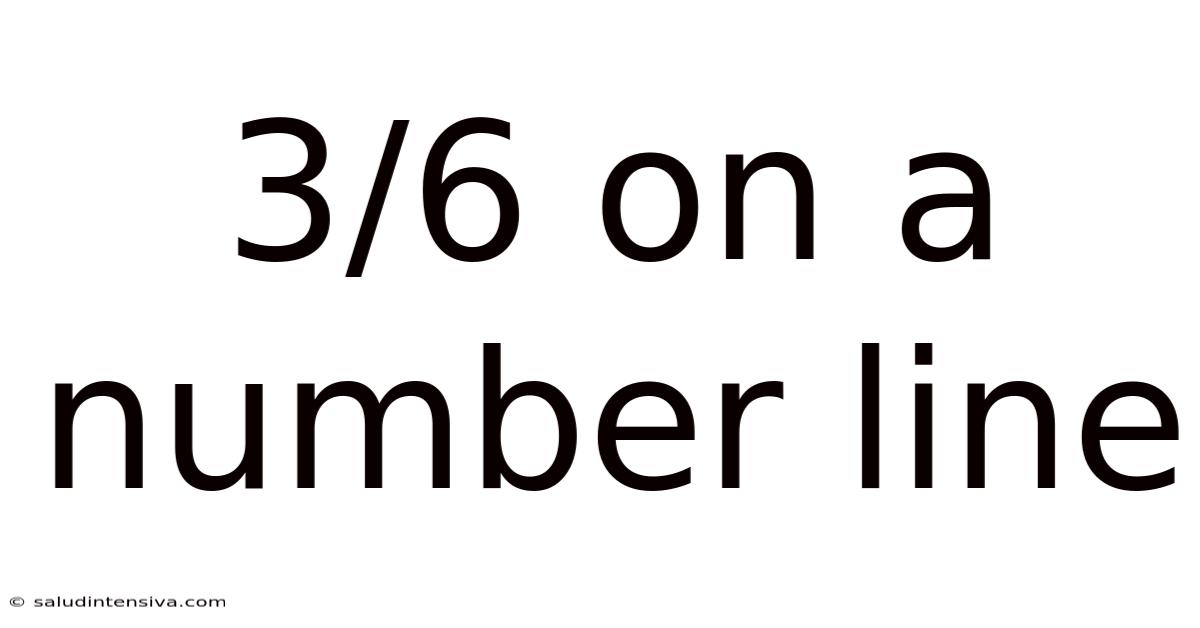
Table of Contents
Understanding 3/6 on the Number Line: A Comprehensive Guide
The seemingly simple fraction 3/6 often presents a challenge for students new to fractions and number lines. This comprehensive guide will demystify the concept, explaining not only where 3/6 sits on a number line but also its equivalence to other fractions and its place within the broader understanding of rational numbers. We'll explore various methods for representing 3/6, delve into the underlying mathematical principles, and answer frequently asked questions. By the end, you'll have a solid grasp of this seemingly simple, yet fundamentally important, fraction.
Introduction to Fractions and Number Lines
Before we pinpoint 3/6 on a number line, let's establish a foundational understanding. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
A number line is a visual representation of numbers, arranged in order from least to greatest. It's a powerful tool for comparing numbers, understanding their relative positions, and visualizing operations. For fractions, the number line typically ranges from 0 to 1, representing the whole.
Locating 3/6 on the Number Line: A Step-by-Step Approach
To accurately place 3/6 on a number line, we need to understand what the fraction represents. 3/6 means we have 3 out of 6 equal parts of a whole. Here's a step-by-step approach:
-
Divide the number line: Draw a number line and label 0 and 1 at its ends. This represents the whole.
-
Divide into equal parts: Since the denominator is 6, divide the space between 0 and 1 into six equal segments. You can use a ruler to ensure accuracy.
-
Count the segments: Start from 0 and count three segments to the right.
-
Mark the point: Place a mark at the end of the third segment. This mark represents the location of 3/6 on the number line.
Visualizing 3/6: Different Representations
While the above method is straightforward, it’s crucial to understand that fractions can be represented visually in various ways. Consider these illustrations:
-
A pie chart: Divide a circle into six equal slices. Shade three of these slices. This visually demonstrates 3/6.
-
A rectangle: Divide a rectangle into six equal columns. Shade three of these columns. This again visually represents 3/6.
-
A set of objects: Imagine six identical objects. If three of them are selected, this also represents 3/6.
These different representations highlight the versatility of fractions and help solidify the understanding that 3/6 represents a specific portion of a whole.
Simplifying Fractions: The Case of 3/6
One of the key concepts in working with fractions is simplification. A fraction is simplified when its numerator and denominator have no common factors other than 1. In the case of 3/6, both the numerator (3) and the denominator (6) are divisible by 3.
Dividing both the numerator and the denominator by 3, we get:
3 ÷ 3 / 6 ÷ 3 = 1/2
This means 3/6 is equivalent to 1/2. This equivalence is crucial; it means that 3/6 and 1/2 represent the same proportion of a whole, and they will occupy the same position on a number line. Therefore, locating 1/2 on a number line is the same as locating 3/6.
Locating 1/2 (equivalent to 3/6) on the Number Line
Locating 1/2 on the number line is simpler than locating 3/6 directly, as it requires only dividing the space between 0 and 1 into two equal parts. The midpoint between 0 and 1 represents 1/2, which is equivalent to 3/6. This reinforces the concept of equivalent fractions.
The Mathematical Principles Behind Equivalent Fractions
The simplification of 3/6 to 1/2 demonstrates a fundamental principle of fractions: equivalent fractions. Equivalent fractions represent the same value despite having different numerators and denominators. They are obtained by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example:
- 1/2 = 2/4 = 3/6 = 4/8 = and so on.
All these fractions represent the same quantity – one-half. This concept is vital in understanding the relationship between different fractions and their positions on a number line.
3/6 in the Context of Rational Numbers
Fractions are a subset of rational numbers. Rational numbers are numbers that can be expressed as a ratio of two integers (where the denominator is not zero). 3/6, being a fraction, is therefore a rational number. Understanding this broader categorization helps place fractions within the larger number system.
Applications of 3/6 and Equivalent Fractions
The concept of 3/6, and its simplified form 1/2, has wide-ranging applications across various fields:
-
Everyday life: Dividing a pizza, sharing sweets, or measuring ingredients in cooking often involves fractions, including halves and their equivalents.
-
Science: Many scientific measurements and calculations involve fractions and ratios.
-
Engineering: Precise calculations in engineering projects frequently utilize fractions and their simplified forms.
-
Finance: Calculating interest, proportions, and percentages often relies on fractional concepts.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and work with. It also allows for easier comparison of fractions. For instance, comparing 3/6 and 5/10 is easier after simplifying both to 1/2.
Q2: Are there other fractions equivalent to 3/6?
A2: Yes, infinitely many! As long as you multiply or divide both the numerator and denominator by the same non-zero number, you'll obtain an equivalent fraction. Examples include 1/2, 2/4, 4/8, 6/12, etc.
Q3: Can I locate 3/6 on a number line without simplifying it?
A3: Yes, absolutely! The method described earlier accurately places 3/6 on a number line, even without simplification. However, simplifying makes the process easier and reduces the risk of errors.
Q4: What if the number line is not from 0 to 1?
A4: If the number line extends beyond 0 and 1, you would simply extend the process. You’d divide the relevant section of the number line (e.g., from 1 to 2) into six equal parts and locate 3/6 from the starting point of that section.
Q5: How does understanding 3/6 help in more advanced math?
A5: Mastering the concept of fractions, including understanding equivalent fractions and their representation on a number line, forms a crucial foundation for more advanced mathematical topics like algebra, calculus, and beyond. It lays the groundwork for understanding ratios, proportions, and more complex numerical operations.
Conclusion: Mastering the Fundamentals
Understanding the location of 3/6 on a number line, along with its simplification to 1/2, is more than just mastering a single fraction; it's about grasping the core concepts of fractions, equivalent fractions, and their representation on a number line. This foundational knowledge is critical for success in mathematics and its various applications in life. By thoroughly understanding these principles and practicing visualization techniques, you can confidently navigate the world of fractions and build a strong mathematical foundation for future learning. Remember, the seemingly simple often holds the key to understanding more complex concepts.
Latest Posts
Latest Posts
-
Lcm Of 27 And 12
Sep 20, 2025
-
How Many Hours In Amonth
Sep 20, 2025
-
Half Of 3 8 In Fraction
Sep 20, 2025
-
90 Days From October 14th
Sep 20, 2025
-
2 To 1 Elliptical Head
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3/6 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.