3 X 3 X 4
saludintensiva
Sep 16, 2025 · 5 min read
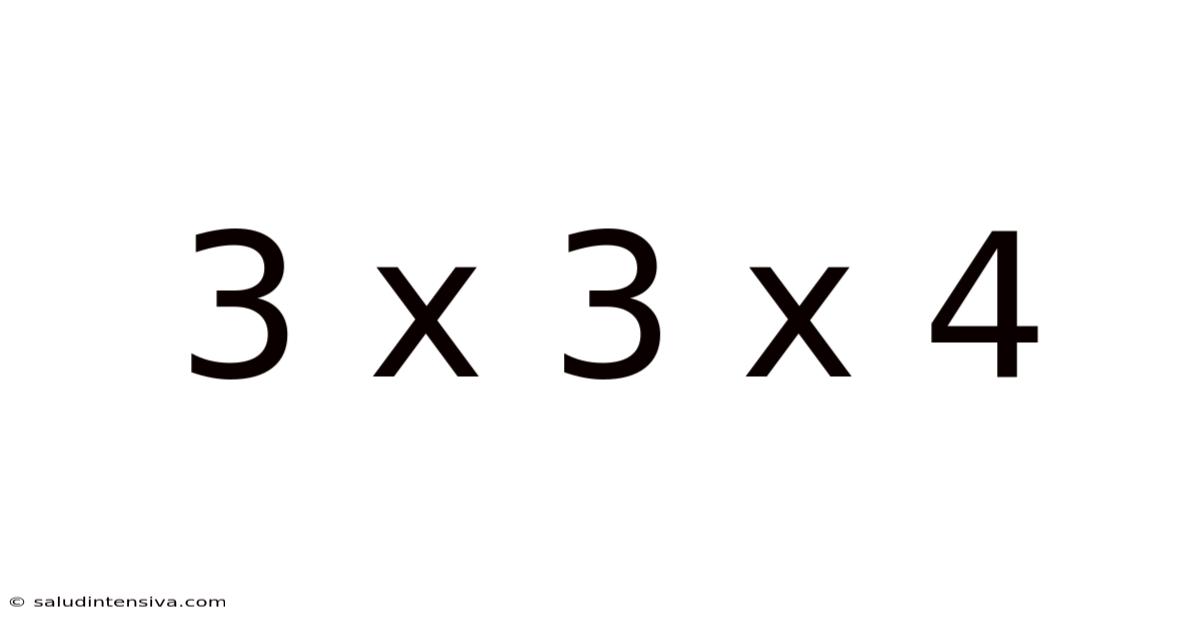
Table of Contents
Decoding 3 x 3 x 4: Exploring Volume, Arrays, and Beyond
This seemingly simple mathematical expression, 3 x 3 x 4, opens doors to a surprisingly wide range of mathematical concepts, from basic volume calculations to more advanced ideas in arrays and combinatorics. This article delves deep into the meaning and implications of 3 x 3 x 4, examining its practical applications and theoretical underpinnings. We’ll explore how understanding this seemingly simple calculation can unlock a deeper appreciation for mathematics and its role in various fields.
Understanding the Fundamentals: Volume and Multiplication
At its most basic level, 3 x 3 x 4 represents a multiplication problem. It can be interpreted as finding the volume of a rectangular prism (or cuboid). Imagine a box:
- 3 units represent the length of the box.
- 3 units represent the width of the box.
- 4 units represent the height of the box.
To find the total volume, we multiply these three dimensions together: 3 x 3 x 4 = 36 cubic units. This means the box can hold 36 cubes, each with sides of 1 unit in length. This fundamental concept of volume calculation is crucial in various fields, from architecture and engineering to logistics and packaging design.
Expanding the Horizons: Arrays and Data Structures
Beyond volume, 3 x 3 x 4 can be visualized as a three-dimensional array. An array is a data structure used in computer science and mathematics to organize data in a grid-like format. In this case, we could imagine a cube divided into 36 smaller cubes, each potentially holding a piece of information.
Consider a scenario where we're tracking the sales of a product across three regions (Region A, Region B, Region C) over three months (Month 1, Month 2, Month 3) and for four different product variations (Product 1, Product 2, Product 3, Product 4). Each smaller cube within our 3 x 3 x 4 array could represent the sales figures for a specific combination (e.g., Region A, Month 1, Product 1). This structured organization allows for easy access and manipulation of data. Understanding arrays is essential in programming, database management, and data analysis.
Delving Deeper: Combinatorics and Permutations
Let’s shift our perspective. Instead of focusing on volume or arrays, let's consider 3 x 3 x 4 in the context of combinatorics. Imagine three choices for color (e.g., red, blue, green), three choices for size (small, medium, large), and four choices for material (wood, plastic, metal, glass). How many possible combinations are there?
The answer is, again, 3 x 3 x 4 = 36. This simple calculation reveals the number of distinct combinations possible when making independent choices from different sets. This concept is crucial in probability, statistics, and even in designing various configurations of products or systems.
Practical Applications Across Disciplines
The seemingly simple calculation 3 x 3 x 4 finds its way into various real-world applications:
- Architecture and Engineering: Calculating the volume of materials needed for construction projects. Designing optimal layouts for spaces using volume calculations.
- Logistics and Supply Chain: Determining the storage capacity of warehouses. Optimizing the packing of goods for shipping and transportation.
- Manufacturing and Production: Calculating the number of components needed for assembly. Designing molds and tooling for manufacturing processes.
- Computer Science: Representing and manipulating data using multi-dimensional arrays. Developing algorithms for processing and analyzing large datasets.
- Game Development: Creating 3D environments and managing game objects within a 3D space. Calculating the space occupied by in-game elements.
- Finance and Economics: Analyzing data sets with multiple variables using multi-dimensional arrays. Modeling financial scenarios with multiple factors.
Exploring Beyond the Basics: Expanding the Dimensions
While we've focused on a 3 x 3 x 4 structure, the principles extend to higher dimensions. Imagine a four-dimensional array, or even higher dimensions, where each dimension represents a different variable. The concept of volume generalizes to hypervolume in higher dimensions. Understanding this broader perspective is essential in advanced mathematics, physics, and computer science.
Mathematical Properties and Relationships
Exploring 3 x 3 x 4 further reveals interesting mathematical properties:
- Factorization: The number 36 (the result of 3 x 3 x 4) can be factored into its prime factors: 2² x 3². This factorization provides insights into the divisibility of 36 and helps in solving related mathematical problems.
- Multiples and Divisors: 36 has numerous multiples and divisors, revealing relationships within the number system. Understanding these relationships is critical in various areas of mathematics, including number theory.
- Geometric Progression: If we consider the sequence 3, 9, 36, we see a geometric progression where each term is obtained by multiplying the previous term by a constant factor (3 in this case). Geometric progressions are widely used in modeling exponential growth or decay.
FAQs: Addressing Common Questions
Q: What are the different ways to calculate 3 x 3 x 4?
A: There are several ways: * Standard multiplication: (3 x 3) x 4 = 9 x 4 = 36 * Associative property: 3 x (3 x 4) = 3 x 12 = 36 * Repeated addition: 9 + 9 + 9 + 9 = 36 (representing four layers of 9 units each)
Q: Can 3 x 3 x 4 be represented graphically?
A: Yes, it can be represented as a rectangular prism or a three-dimensional array, as discussed earlier. This visual representation enhances understanding and provides a concrete way to interpret the calculation.
Q: What are some real-world examples beyond those mentioned?
A: Think about arranging items on shelves, stacking boxes in a warehouse, or even planning seating arrangements in a room. The principles of 3 x 3 x 4 apply whenever you need to organize items in a three-dimensional space.
Conclusion: Unlocking the Potential of Simple Calculations
The seemingly simple expression, 3 x 3 x 4, opens up a wide range of mathematical and practical applications. From basic volume calculations to advanced concepts in arrays, combinatorics, and higher-dimensional spaces, this seemingly simple calculation forms a foundation for understanding more complex ideas. By exploring its different interpretations and applications, we gain a deeper appreciation for the power and versatility of mathematics in our world. Understanding these fundamental principles is crucial for success in various fields, highlighting the importance of grasping even the most basic mathematical concepts. The journey from a simple multiplication problem to the complex world of data structures and higher dimensions underscores the enriching and expanding nature of mathematical exploration.
Latest Posts
Latest Posts
-
Calculating Cubic Yards Of Sand
Sep 16, 2025
-
8 Years Ago From Today
Sep 16, 2025
-
22 Percent As A Fraction
Sep 16, 2025
-
3 4 X 1 6
Sep 16, 2025
-
Simplest Form Of 12 15
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 X 3 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.