33 1 3 Mixed Fraction
saludintensiva
Sep 20, 2025 · 5 min read
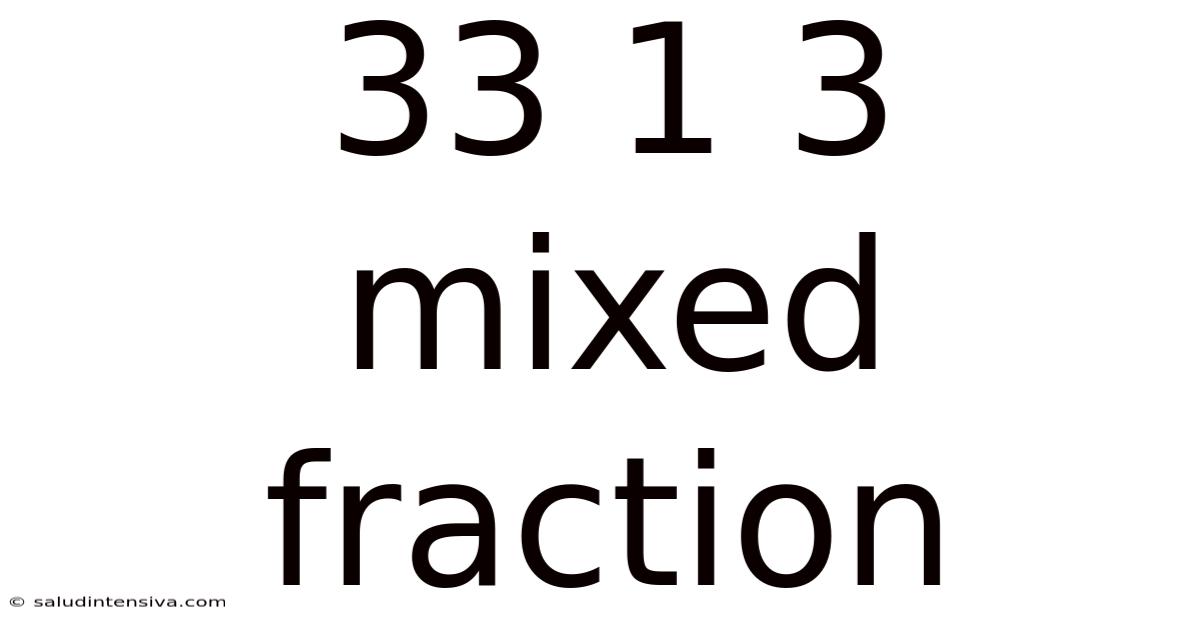
Table of Contents
Decoding the Mystery of Mixed Fractions: A Deep Dive into 33 1/3
Understanding mixed fractions is a cornerstone of mathematical literacy. This comprehensive guide will explore the intricacies of mixed fractions, specifically focusing on the common example of 33 1/3. We'll delve into its meaning, conversion methods, practical applications, and address frequently asked questions. By the end, you'll not only grasp the concept of 33 1/3 but also gain a robust understanding of mixed fractions in general.
What is a Mixed Fraction?
A mixed fraction represents a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1/2, 3/4, and 2/5 are all proper fractions. A mixed fraction combines this proper fraction with a whole number. So, 33 1/3 means 33 whole units plus an additional one-third of a unit.
Understanding 33 1/3
The mixed fraction 33 1/3 represents thirty-three whole units and one-third of another unit. Imagine you have 33 whole pizzas, and one more pizza that has been cut into three equal slices; you have one of those slices. That's visually representing 33 1/3. This seemingly simple fraction finds applications in various areas, from calculating percentages to understanding proportions in everyday life.
Converting Mixed Fractions to Improper Fractions
Mixed fractions can be converted into improper fractions, where the numerator is larger than or equal to the denominator. This form is often more useful for calculations. To convert 33 1/3 to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: 33 x 3 = 99
- Add the numerator: 99 + 1 = 100
- Keep the same denominator: The denominator remains 3.
Therefore, 33 1/3 is equivalent to the improper fraction 100/3.
Converting Improper Fractions to Mixed Fractions
The reverse process, converting an improper fraction to a mixed fraction, is equally important. Let's take the example of 100/3:
- Divide the numerator by the denominator: 100 ÷ 3 = 33 with a remainder of 1.
- The quotient becomes the whole number: 33 is the whole number part.
- The remainder becomes the numerator: 1 is the numerator of the fraction.
- The denominator remains the same: The denominator remains 3.
Thus, 100/3 converts back to the mixed fraction 33 1/3.
Decimal Representation of 33 1/3
Mixed fractions can also be expressed as decimals. To convert 33 1/3 to a decimal, you can either convert it to an improper fraction first and then divide, or directly divide the fraction part.
- Improper Fraction Method: 100/3 ≈ 33.333... (The 3 repeats infinitely)
- Direct Division: 1/3 ≈ 0.333... Adding this to 33 gives us approximately 33.333...
Applications of 33 1/3 and Mixed Fractions
Mixed fractions, including 33 1/3, are frequently encountered in various real-world scenarios:
- Percentages: 33 1/3 is one-third, which is equivalent to approximately 33.33%. This percentage is commonly used in discounts, sales, and proportions.
- Measurements: When measuring lengths, weights, or volumes, fractional parts are often encountered. A recipe might call for 33 1/3 grams of an ingredient.
- Finance: Calculations involving interest rates, dividends, or stock prices can involve mixed fractions.
- Geometry: Calculations involving areas, volumes, and angles might utilize mixed fractions.
- Everyday Life: Sharing items equally often results in fractional portions, leading to the use of mixed fractions.
Working with 33 1/3 in Calculations
Adding, subtracting, multiplying, and dividing mixed fractions requires careful attention. It’s generally easier to convert mixed fractions to improper fractions before performing calculations, then convert the result back to a mixed fraction if needed.
Addition and Subtraction:
To add or subtract mixed fractions, first convert them to improper fractions, then find a common denominator, and add or subtract the numerators. Finally, convert the result back to a mixed fraction.
Example: 22 2/3 + 11 1/3
- Convert to improper fractions: (68/3) + (34/3)
- Add the numerators: 102/3
- Convert back to a mixed fraction: 34
Multiplication and Division:
Multiplication and division of mixed fractions are more straightforward when the fractions are first converted to improper fractions.
Example: Multiplication 2 1/3 * 3 1/3
- Convert to improper fractions: (7/3) * (10/3)
- Multiply numerators and denominators: 70/9
- Convert to a mixed fraction: 7 7/9
Example: Division 2 1/3 ÷ 1 1/3
- Convert to improper fractions: (7/3) ÷ (4/3)
- Invert the second fraction and multiply: (7/3) * (3/4)
- Simplify and convert to a mixed fraction: 7/4 = 1 3/4
Frequently Asked Questions (FAQs)
Q: What is the simplest form of 33 1/3?
A: While 33 1/3 is a mixed fraction, it's already in its simplest form because the fraction part (1/3) cannot be reduced further.
Q: How do I convert 33 1/3 to a percentage?
A: 33 1/3 is equivalent to 1/3. To convert 1/3 to a percentage, divide 1 by 3 (0.333...) and multiply by 100 to get approximately 33.33%.
Q: Can 33 1/3 be expressed as a terminating decimal?
A: No, 33 1/3 cannot be expressed as a terminating decimal. The decimal representation is a repeating decimal: 33.333...
Q: What are some common mistakes when working with mixed fractions?
A: Common mistakes include forgetting to convert mixed fractions to improper fractions before performing calculations, incorrectly adding or subtracting the whole numbers and fractional parts separately, and failing to simplify the resulting fraction.
Conclusion
Understanding mixed fractions is essential for various mathematical applications. This detailed exploration of 33 1/3, including its conversion to improper fractions and decimals, and its use in calculations, provides a strong foundation for working with mixed fractions in general. Remember to practice regularly and use the methods described above to master this crucial mathematical concept. The seemingly simple 33 1/3 opens a door to a deeper comprehension of fractions and their broad applicability in numerous fields. With consistent practice and a clear understanding of the underlying principles, you can confidently tackle any mixed fraction challenge.
Latest Posts
Latest Posts
-
Lcm Of 27 And 12
Sep 20, 2025
-
How Many Hours In Amonth
Sep 20, 2025
-
Half Of 3 8 In Fraction
Sep 20, 2025
-
90 Days From October 14th
Sep 20, 2025
-
2 To 1 Elliptical Head
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 33 1 3 Mixed Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.