4 10 In Simplest Form
saludintensiva
Sep 14, 2025 · 5 min read
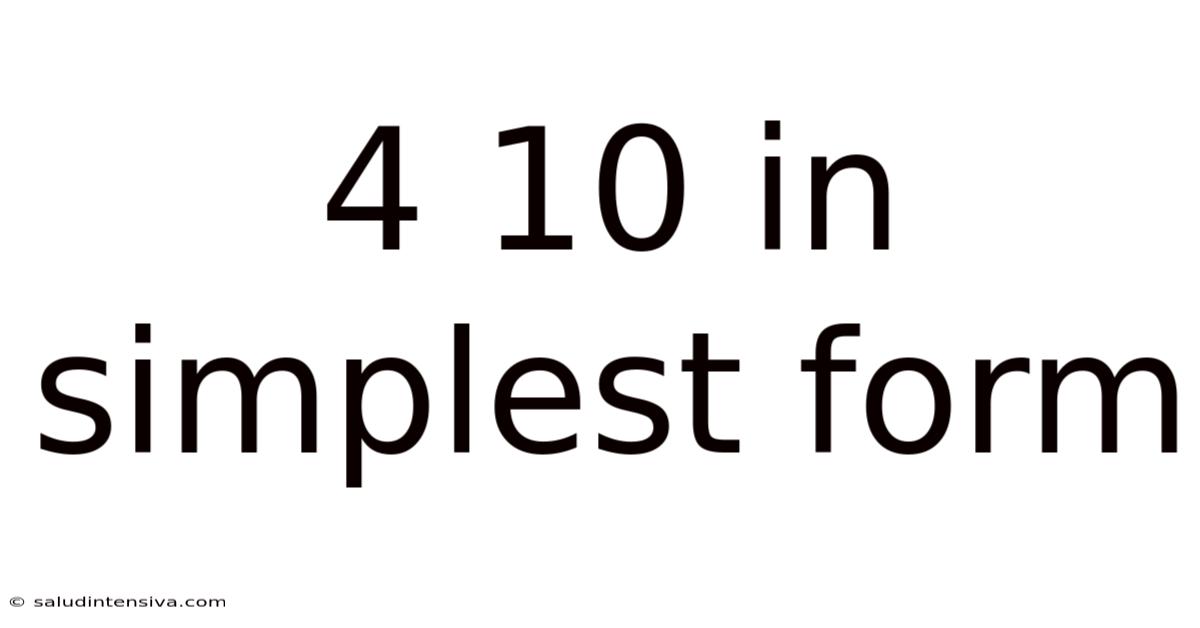
Table of Contents
Simplifying Fractions: A Deep Dive into 4/10
Understanding fractions is a fundamental building block in mathematics, crucial for everything from basic arithmetic to advanced calculus. This article will explore the simplification of fractions, specifically focusing on how to reduce 4/10 to its simplest form. We'll go beyond a simple answer, delving into the underlying principles and providing a comprehensive understanding of the process, making it accessible to learners of all levels.
Introduction: What Does "Simplest Form" Mean?
When we talk about simplifying a fraction, we're aiming to express it in its simplest form. This means finding an equivalent fraction where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In other words, we're looking for the fraction's smallest possible representation. Simplifying fractions isn't just about aesthetics; it makes calculations easier and improves understanding by presenting the fraction in its most concise and manageable form. This is especially helpful when working with larger numbers or more complex calculations. The fraction 4/10, while perfectly valid, can be simplified to a smaller, more manageable equivalent.
Understanding Factors and Greatest Common Factors (GCF)
Before we simplify 4/10, let's refresh our understanding of factors. Factors are numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. To find the simplest form of a fraction, we need to identify the greatest common factor (GCF) of the numerator and the denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's find the factors of 4 and 10:
- Factors of 4: 1, 2, 4
- Factors of 10: 1, 2, 5, 10
By comparing the lists, we can see that the largest number that appears in both lists is 2. Therefore, the GCF of 4 and 10 is 2.
Step-by-Step Simplification of 4/10
Now that we've identified the GCF, simplifying 4/10 becomes a straightforward process:
-
Divide the numerator and denominator by the GCF: We divide both 4 and 10 by their GCF, which is 2.
4 ÷ 2 = 2 10 ÷ 2 = 5
-
Write the simplified fraction: The result of this division gives us the simplified fraction: 2/5.
Therefore, 4/10 simplified to its simplest form is 2/5.
Visual Representation: Understanding Equivalence
Imagine you have a pizza cut into 10 equal slices. The fraction 4/10 represents 4 out of 10 slices. If you group those 4 slices into two pairs, you'll have two groups of two slices each. Now, consider the pizza recut into 5 larger slices. Each larger slice is equivalent to two of the original smaller slices. Your two groups of two smaller slices now represent 2 out of the 5 larger slices, visually demonstrating the equivalence of 4/10 and 2/5.
Different Methods for Finding the GCF
While the method of listing factors works well for smaller numbers, it can become cumbersome with larger numbers. Here are a couple of alternative methods for finding the GCF:
-
Prime Factorization: This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves). The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 10: 2 x 5
The only common prime factor is 2, and its lowest power is 2¹ (or simply 2). Therefore, the GCF is 2.
-
Euclidean Algorithm: This is a more efficient method for finding the GCF of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean Algorithm to 4 and 10:
10 ÷ 4 = 2 with a remainder of 2 4 ÷ 2 = 2 with a remainder of 0
The last non-zero remainder is 2, so the GCF is 2.
The Importance of Simplifying Fractions
Simplifying fractions is more than just a mathematical procedure; it's a crucial skill with practical applications:
-
Clarity and Understanding: A simplified fraction provides a clearer and more concise representation of a quantity. It makes it easier to grasp the magnitude of the fraction and compare it to other fractions.
-
Easier Calculations: Simplifying fractions before performing operations like addition, subtraction, multiplication, or division significantly reduces the complexity of the calculations and minimizes the risk of errors.
-
Problem Solving: In real-world problem-solving, simplified fractions often lead to simpler and more elegant solutions. For instance, in scenarios involving ratios, proportions, or percentages, a simplified fraction makes the relationships between quantities more readily apparent.
Frequently Asked Questions (FAQ)
-
Q: What if the numerator is 0?
A: If the numerator is 0, the fraction is equal to 0, regardless of the denominator. There's no need for simplification in this case.
-
Q: What if the numerator and denominator are the same?
A: If the numerator and the denominator are the same, the fraction simplifies to 1. For example, 5/5 = 1.
-
Q: Can I simplify a fraction by only dividing the numerator or only dividing the denominator?
A: No, to simplify a fraction correctly, you must divide both the numerator and the denominator by the same number (their GCF). Dividing only one part will change the value of the fraction.
-
Q: Are there fractions that cannot be simplified?
A: Yes, fractions where the numerator and denominator have no common factors other than 1 are already in their simplest form. For example, 3/7 is already in its simplest form.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill that underpins a strong understanding of mathematics. By understanding the concept of the greatest common factor and employing efficient methods for finding it, you can confidently simplify fractions of any size. The process of simplifying 4/10 to 2/5, as detailed above, demonstrates a clear and methodical approach. This skill is not just about getting the right answer but also about developing a deeper understanding of numerical relationships and preparing you for more complex mathematical concepts in the future. Remember that practice is key – the more you work with fractions, the more proficient and confident you'll become. So, grab a pencil and paper and start practicing! You'll quickly find that simplifying fractions becomes second nature.
Latest Posts
Latest Posts
-
4 12 As A Percent
Sep 14, 2025
-
2 50 As A Percentage
Sep 14, 2025
-
Gcf Of 75 And 90
Sep 14, 2025
-
Hcf Of 15 And 18
Sep 14, 2025
-
Write 2 As A Decimal
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 10 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.