5 6 Divided By 7
saludintensiva
Sep 16, 2025 · 6 min read
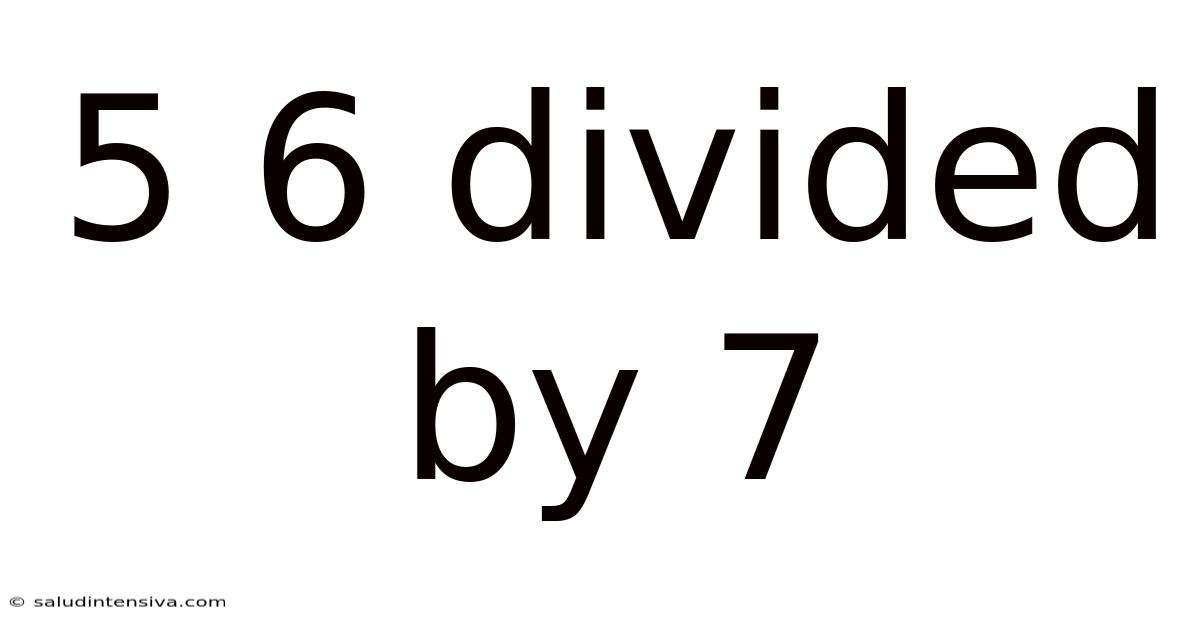
Table of Contents
Deconstructing Division: A Deep Dive into 56 Divided by 7
Understanding division is fundamental to mathematics, forming the bedrock for more complex calculations and problem-solving. This article delves into the seemingly simple equation of 56 divided by 7, exploring not just the answer but the underlying principles, various methods of calculation, and its practical applications. We'll journey from basic arithmetic to exploring the conceptual meaning of division, ensuring a comprehensive understanding for learners of all levels.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the equation 56 ÷ 7 (or 56/7), we are asking: "How many times does 7 fit into 56?" The answer, as we will demonstrate, is 8. But the process of arriving at this answer, and the understanding of what it represents, is far more significant than simply stating the result. This exploration will cover various methods, including long division, repeated subtraction, and visual representations. We will also delve into the conceptual meaning, discussing its relationship to multiplication and its relevance in real-world applications.
Method 1: Long Division - The Classic Approach
Long division is a standard algorithm for dividing larger numbers. Let's apply it to 56 ÷ 7:
-
Set up the problem: Write the dividend (56) inside the long division symbol (⟌) and the divisor (7) outside.
7⟌56 -
Divide the tens digit: How many times does 7 go into 5? It doesn't go in at all, so we move to the next digit.
-
Divide the tens and ones digit: Now consider 56. How many times does 7 go into 56? The answer is 8 (7 x 8 = 56). Write the 8 above the 6.
8 7⟌56 -
Multiply: Multiply the quotient (8) by the divisor (7): 8 x 7 = 56. Write this below the 56.
8 7⟌56 56 -
Subtract: Subtract the result (56) from the dividend (56): 56 - 56 = 0. Write the result below.
8 7⟌56 56 0 -
The answer: The remainder is 0, indicating that 7 divides 56 evenly. Therefore, 56 ÷ 7 = 8.
Method 2: Repeated Subtraction - A Conceptual Approach
Repeated subtraction provides a more intuitive understanding of division. We repeatedly subtract the divisor (7) from the dividend (56) until we reach zero. Each subtraction represents one instance of the divisor fitting into the dividend.
-
Start with the dividend: Begin with 56.
-
Subtract the divisor repeatedly:
- 56 - 7 = 49
- 49 - 7 = 42
- 42 - 7 = 35
- 35 - 7 = 28
- 28 - 7 = 21
- 21 - 7 = 14
- 14 - 7 = 7
- 7 - 7 = 0
-
Count the subtractions: We subtracted 7 a total of 8 times to reach zero. Therefore, 56 ÷ 7 = 8.
Method 3: Visual Representation - Using Groups
Visualizing the problem can be particularly helpful for younger learners. Imagine you have 56 objects (e.g., candies). You want to divide these candies equally among 7 friends.
-
Create groups: Start grouping the candies into sets of 7.
-
Count the groups: You'll create 8 groups of 7 candies each.
-
The answer: Each friend gets 8 candies, confirming that 56 ÷ 7 = 8.
The Relationship Between Division and Multiplication
Division and multiplication are inverse operations. This means that division "undoes" multiplication, and vice versa. If 7 x 8 = 56, then 56 ÷ 7 = 8, and 56 ÷ 8 = 7. Understanding this relationship is crucial for grasping the concept of division. It allows you to check your answers and to solve problems using either operation depending on which is more convenient.
Real-World Applications of Division
Division is used extensively in various real-world situations:
- Sharing equally: Dividing treats among friends, splitting a bill, or distributing resources fairly.
- Calculating averages: Finding the average score on a test, the average speed, or the average temperature.
- Unit conversion: Converting larger units (kilometers) to smaller units (meters), or vice versa.
- Scaling recipes: Adjusting recipe quantities to serve a larger or smaller number of people.
- Calculating rates: Determining speed (distance divided by time), unit price (total cost divided by quantity), or fuel efficiency (distance divided by fuel consumption).
Understanding Remainders
While 56 divides evenly by 7, not all division problems result in a whole number. Sometimes, a remainder is left over. For example, if we divide 58 by 7:
- 7 goes into 58 eight times (7 x 8 = 56).
- Subtracting 56 from 58 leaves a remainder of 2.
We would express this as 58 ÷ 7 = 8 with a remainder of 2, or sometimes written as 8 R2. Remainders are important because they represent the portion of the dividend that couldn't be divided evenly by the divisor. Understanding remainders is crucial in situations where equal distribution isn't possible, such as arranging objects into equal rows or determining how many buses are needed to transport a group of people.
Extending the Concept: Dividing Larger Numbers
The principles we've explored with 56 ÷ 7 apply to dividing larger numbers as well. The long division method, in particular, remains a powerful tool. While the steps might become more complex with more digits, the core concepts—division, multiplication, and subtraction—remain the same. Practice and familiarity are key to mastering division with larger numbers. Repeated subtraction becomes less practical with significantly larger numbers, but it still serves as a valuable conceptual tool for understanding the process.
Frequently Asked Questions (FAQs)
Q: What is the inverse operation of division?
A: The inverse operation of division is multiplication.
Q: What happens if the divisor is larger than the dividend?
A: If the divisor is larger than the dividend, the result is a fraction or decimal less than 1. For instance, 5 ÷ 7 is approximately 0.714.
Q: How do I handle remainders in division problems?
A: Remainders represent the portion of the dividend that could not be divided evenly by the divisor. They can be expressed as a remainder (e.g., R2), a fraction (e.g., 2/7), or a decimal (e.g., approximately 0.286). The best way to represent the remainder depends on the context of the problem.
Q: Is there a quicker way to divide than long division?
A: For simpler divisions, mental math or multiplication facts can be used. Calculators are also efficient tools for larger or more complex divisions.
Conclusion: Mastering the Fundamentals
The seemingly simple equation 56 divided by 7 offers a gateway to understanding the fundamental principles of division. By exploring various methods—long division, repeated subtraction, and visual representations—we gain a multifaceted understanding of this essential arithmetic operation. This knowledge is not just about finding the answer (8); it's about grasping the underlying concepts, recognizing its connection to multiplication, and appreciating its extensive applications in everyday life and more advanced mathematical concepts. Mastering division builds a strong foundation for future mathematical endeavors, allowing you to confidently tackle more complex problems and apply this crucial skill in various real-world scenarios. The journey from understanding the basic division of 56 by 7 to tackling more complex mathematical problems is a testament to the power of building a strong foundation in fundamental arithmetic.
Latest Posts
Latest Posts
-
7 25 As A Decimal
Sep 17, 2025
-
What Are Multiples Of 60
Sep 17, 2025
-
Gcd Of 2 And 4
Sep 17, 2025
-
What Is 3 4 In Percentage
Sep 17, 2025
-
Calculate A Ratio In Excel
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.