5 Divided By 2 3
saludintensiva
Sep 18, 2025 · 5 min read
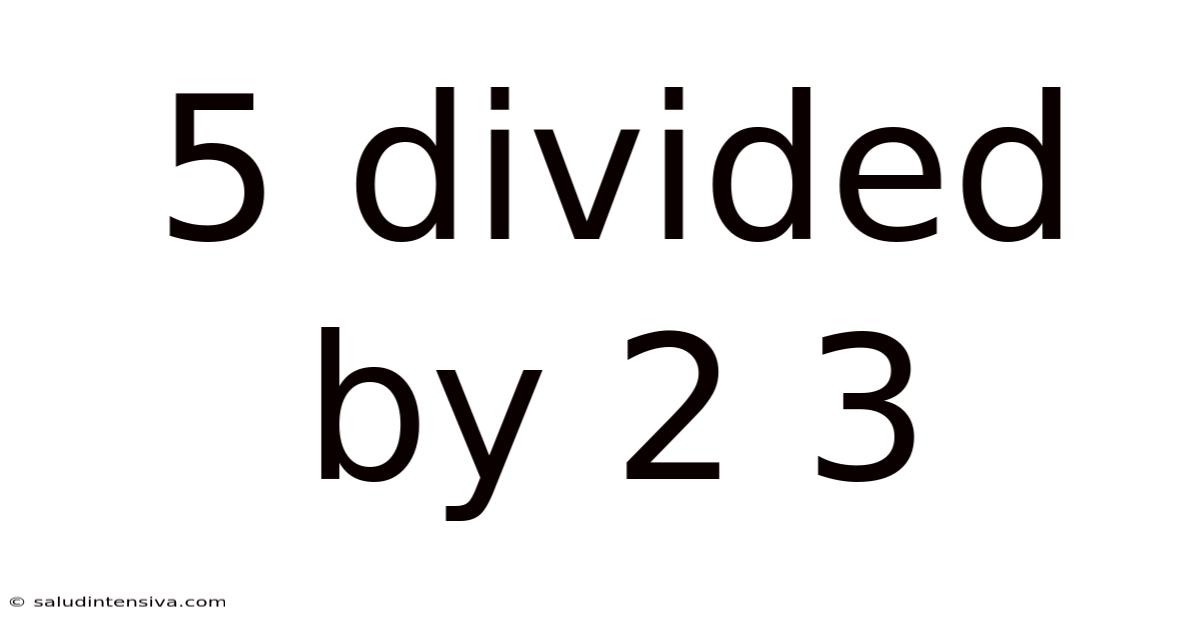
Table of Contents
Decoding 5 Divided by 2 3: A Deep Dive into Mixed Numbers and Decimal Conversions
This article explores the seemingly simple calculation of 5 divided by 2 3/5, delving into the intricacies of mixed number division, showcasing different methods for solving it, and providing a thorough understanding of the underlying mathematical principles. Understanding this seemingly basic problem unlocks a broader understanding of fractions, decimals, and their inter-relationships. This will be particularly useful for students learning about arithmetic operations with mixed numbers, and provides a comprehensive guide for anyone wanting to refresh their understanding of this core mathematical concept.
Understanding the Problem: 5 ÷ 2 3/5
The problem, 5 divided by 2 3/5, involves dividing a whole number (5) by a mixed number (2 3/5). A mixed number combines a whole number and a fraction. This seemingly straightforward calculation requires a solid grasp of fraction manipulation and division principles. We will unpack various methods to solve this, highlighting the rationale behind each step.
Method 1: Converting to Improper Fractions
The most common and arguably easiest method involves converting both the mixed number and the whole number into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert the mixed number to an improper fraction.
To convert 2 3/5 to an improper fraction, we multiply the whole number (2) by the denominator (5), add the numerator (3), and keep the same denominator:
(2 * 5) + 3 = 13
So, 2 3/5 becomes 13/5.
Step 2: Convert the whole number to an improper fraction.
We can express the whole number 5 as an improper fraction by placing it over 1: 5/1.
Step 3: Perform the division.
Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping its numerator and denominator. The reciprocal of 13/5 is 5/13.
Therefore, the calculation becomes:
5/1 ÷ 13/5 = 5/1 * 5/13 = 25/13
Step 4: Convert the improper fraction to a mixed number (optional).
The improper fraction 25/13 can be converted back to a mixed number by dividing the numerator (25) by the denominator (13):
25 ÷ 13 = 1 with a remainder of 12.
Thus, 25/13 is equivalent to 1 12/13.
Therefore, 5 divided by 2 3/5 is 1 12/13.
Method 2: Using Decimal Conversions
Another method involves converting both the whole number and the mixed number into decimals before performing the division.
Step 1: Convert the mixed number to a decimal.
To convert 2 3/5 to a decimal, we first convert the fraction 3/5 to a decimal by dividing 3 by 5:
3 ÷ 5 = 0.6
Therefore, 2 3/5 is equal to 2.6.
Step 2: Perform the division.
Now we divide 5 by 2.6:
5 ÷ 2.6 ≈ 1.923
This method provides a decimal approximation. The slight difference from the fractional answer (1 12/13) is due to rounding in the decimal conversion.
Method 3: Long Division with Mixed Numbers (Advanced Method)
This method demonstrates how to perform long division directly with mixed numbers, offering a more visual approach to understanding the division process. While more complex, it strengthens foundational arithmetic skills.
This method requires a nuanced understanding of long division and might be less efficient than the previous methods for this specific problem. However, it provides valuable insight into the underlying mechanics of division. It is best explored with a pencil and paper due to the spatial requirements of the long division process.
The process is conceptually similar to standard long division but necessitates careful handling of the fractional components. It often involves converting the mixed number into an improper fraction at some stage of the calculation, thereby transitioning into a process similar to Method 1.
The Importance of Understanding Mixed Numbers and Fractions
Understanding mixed numbers and their manipulation is fundamental to various mathematical concepts. It forms the basis for:
- Algebra: Solving equations involving fractions and variables.
- Geometry: Calculating areas, volumes, and other geometric properties.
- Calculus: Working with derivatives and integrals that involve fractions.
- Real-world applications: Numerous everyday scenarios involve fractions, such as cooking recipes, measuring materials, and calculating proportions.
Frequently Asked Questions (FAQ)
Q1: Why are there different methods to solve this problem?
A1: Different methods offer alternative approaches to solving the same problem. Choosing a method depends on individual preferences and the context of the problem. Some methods are more efficient than others, particularly when dealing with more complex calculations.
Q2: Which method is the "best" method?
A2: There isn't a single "best" method. The optimal approach depends on individual comfort and the specific problem's context. Converting to improper fractions (Method 1) is generally efficient and widely applicable. Decimal conversion (Method 2) is useful when dealing with real-world applications requiring approximate answers.
Q3: What if the divisor (2 3/5) was a smaller number? Would the solution still be a mixed number?
A3: The nature of the solution (mixed number, whole number, or decimal) depends on the relationship between the dividend (5) and the divisor (2 3/5). If the divisor were smaller, the resulting quotient could potentially be a whole number or a larger mixed number.
Q4: Can this type of problem involve negative numbers?
A4: Yes, the dividend or the divisor could be negative numbers. The rules of signs in division still apply (positive divided by positive = positive, positive divided by negative = negative, etc.).
Conclusion
Solving 5 divided by 2 3/5 illustrates the importance of understanding fraction manipulation and different computational strategies. Whether you choose to convert to improper fractions, use decimal conversions, or even tackle the long division method, mastering these techniques is critical for success in mathematics and its diverse applications. Remember, the goal isn't just to find the answer (1 12/13), but to understand the underlying mathematical principles and to build a solid foundation for more advanced mathematical concepts. This understanding extends beyond the classroom, enriching our ability to solve problems in various aspects of our lives. Choosing the right method often comes down to personal preference and the context of the problem, demonstrating the multifaceted nature of mathematics and the beauty of diverse approaches to problem-solving.
Latest Posts
Latest Posts
-
Is 7 8 Greater Than 5 8
Sep 18, 2025
-
What Percent Is 1 10
Sep 18, 2025
-
What Is 5 6 Of 3 4
Sep 18, 2025
-
17 Percent As A Fraction
Sep 18, 2025
-
Numbers From Least To Greatest
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.