6 3 In Simplest Form
saludintensiva
Sep 15, 2025 · 6 min read
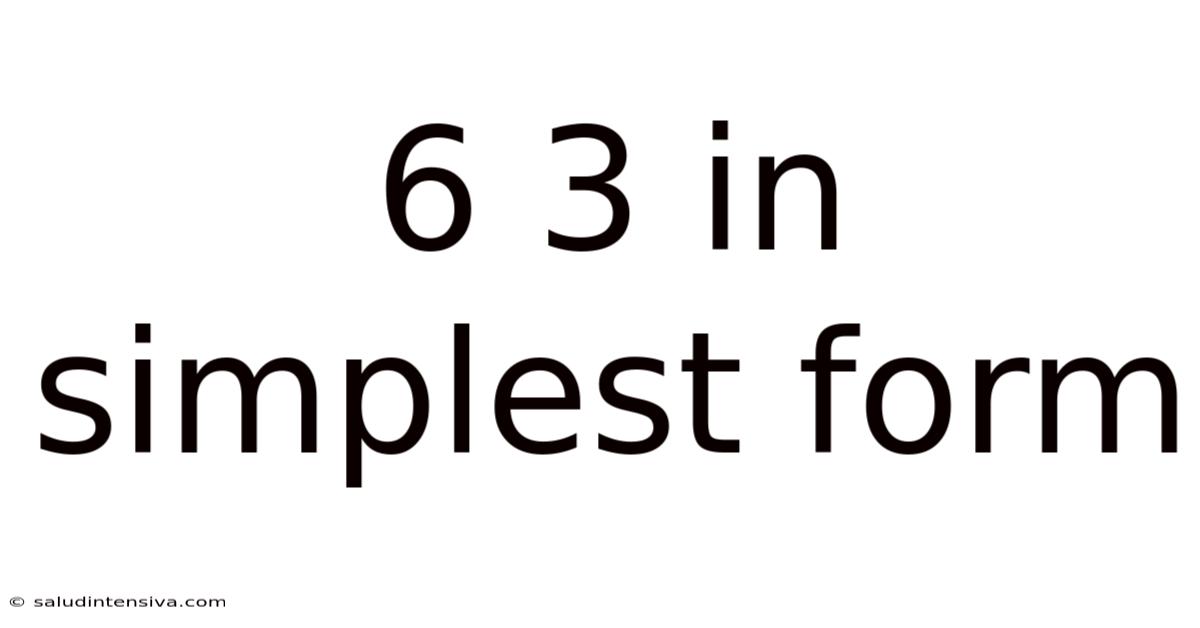
Table of Contents
Understanding Fractions: Simplifying 6/3 to its Simplest Form
Fractions are a fundamental concept in mathematics, representing parts of a whole. Learning to manipulate and simplify fractions is crucial for success in various mathematical fields. This article will delve into the process of simplifying fractions, using the example of 6/3, explaining the underlying principles, and providing a broader understanding of fraction simplification. We'll cover what constitutes a fraction, how to simplify one, and why simplifying is important. By the end, you'll not only know the simplest form of 6/3 but also possess the tools to tackle any fraction simplification problem.
What is a Fraction?
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (1) signifies that we're considering one of those parts.
Understanding 6/3
The fraction 6/3 represents six parts out of a total of three parts. This might seem unusual at first glance, as it implies more parts than the whole is divided into. This is where the importance of simplifying fractions comes in. Simplifying helps to express the fraction in its most concise and easily understandable form.
Simplifying Fractions: The Greatest Common Divisor (GCD)
Simplifying a fraction involves reducing it to its lowest terms. This is achieved by finding the greatest common divisor (GCD), also known as the highest common factor (HCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 6 and 3, we can list the factors of each number:
- Factors of 6: 1, 2, 3, 6
- Factors of 3: 1, 3
The largest number that appears in both lists is 3. Therefore, the GCD of 6 and 3 is 3.
Simplifying 6/3
Now that we've found the GCD, we can simplify the fraction 6/3 by dividing both the numerator and the denominator by the GCD:
6 ÷ 3 = 2 3 ÷ 3 = 1
Therefore, the simplified form of 6/3 is 2/1, which is equivalent to 2.
Why Simplify Fractions?
Simplifying fractions is essential for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret. A simple fraction like 2 is much clearer than the equivalent fraction 6/3.
- Efficiency: Simplified fractions make calculations simpler and faster. Working with 2 is considerably easier than working with 6/3, especially in more complex mathematical operations.
- Standardization: Simplifying fractions ensures consistency and allows for easier comparison of fractions.
- Accuracy: In some contexts, such as in engineering or scientific calculations, unsimplified fractions can lead to errors in measurement or calculations.
Methods for Finding the GCD
While listing factors works well for smaller numbers, it can become cumbersome for larger numbers. Here are some alternative methods for finding the GCD:
-
Prime Factorization: This method involves breaking down the numerator and denominator into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
For example, let's find the GCD of 12 and 18:
- Prime factorization of 12: 2 x 2 x 3
- Prime factorization of 18: 2 x 3 x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ = 2, and the lowest power of 3 is 3¹ = 3. Therefore, the GCD is 2 x 3 = 6.
-
Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 48 and 18 using the Euclidean Algorithm:
- 48 ÷ 18 = 2 with a remainder of 12
- 18 ÷ 12 = 1 with a remainder of 6
- 12 ÷ 6 = 2 with a remainder of 0
The last non-zero remainder is 6, so the GCD of 48 and 18 is 6.
Improper Fractions and Mixed Numbers
The fraction 6/3 is an example of an improper fraction, where the numerator is greater than or equal to the denominator. When simplifying an improper fraction, you often end up with a whole number, as in this case. Another way to express an improper fraction is as a mixed number. A mixed number combines a whole number and a proper fraction (where the numerator is less than the denominator). While 6/3 simplifies to 2, it could also be expressed as 2 0/3. However, including the 0/3 is redundant and thus unnecessary.
Applying Fraction Simplification in Real-World Scenarios
Fraction simplification isn't just an abstract mathematical concept; it has practical applications in various real-world scenarios:
- Cooking and Baking: Recipes often require fractions of ingredients. Simplifying fractions ensures accurate measurements.
- Construction and Engineering: Precise measurements and calculations are vital in construction and engineering projects. Simplifying fractions helps to avoid errors and ensure accuracy.
- Finance: Calculations involving percentages and proportions often use fractions. Simplifying fractions makes these calculations easier and more efficient.
- Data Analysis: Data analysis often involves working with proportions and ratios, which are often represented as fractions. Simplifying fractions enhances the clarity and interpretability of the data.
Frequently Asked Questions (FAQ)
Q: What if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, then the fraction is already in its simplest form and cannot be simplified further. Such a fraction is called a reduced fraction.
Q: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
A: Yes, you can divide by any common factor, but to get the simplest form, you must divide by the greatest common factor. Dividing by a smaller common factor will result in a fraction that is still reducible.
Q: What if I have a negative fraction?
A: The process remains the same. Find the GCD of the absolute values of the numerator and denominator, and simplify. The negative sign remains with the fraction. For example, -6/3 simplifies to -2.
Q: Are there any online tools to simplify fractions?
A: Yes, many websites and apps offer fraction simplification calculators. These can be useful for checking your work or simplifying larger fractions. However, understanding the underlying principles is more important than relying solely on tools.
Conclusion
Simplifying fractions, as illustrated with the example of 6/3, is a fundamental skill in mathematics. It's not just about reducing numbers; it's about improving clarity, efficiency, and accuracy in mathematical operations and real-world applications. By mastering the techniques for finding the greatest common divisor and understanding the concept of improper fractions and mixed numbers, you’ll build a strong foundation for more advanced mathematical concepts. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you will become. The seemingly simple act of simplifying 6/3 to 2 opens doors to a deeper understanding of numbers and their relationships.
Latest Posts
Latest Posts
-
75 100 As A Decimal
Sep 15, 2025
-
Lcm Of 13 And 9
Sep 15, 2025
-
7 1 2 As A Decimal
Sep 15, 2025
-
Gcf Of 12 And 32
Sep 15, 2025
-
Convert 64 Into A Fraction
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6 3 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.