7 1/2 As A Decimal
saludintensiva
Sep 15, 2025 · 5 min read
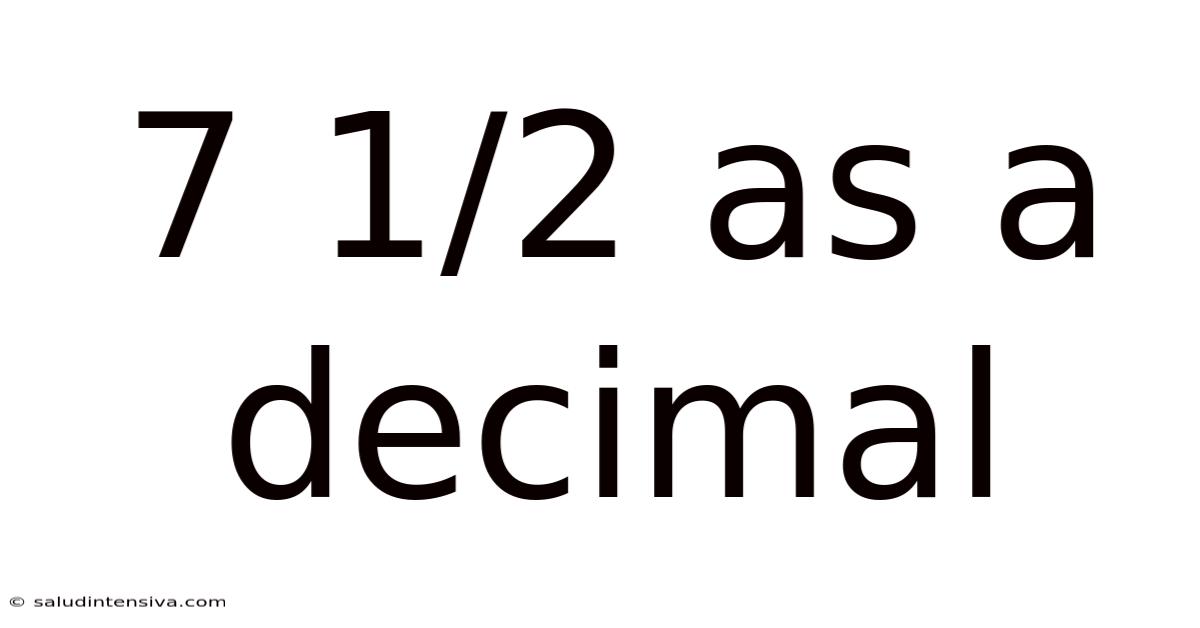
Table of Contents
7 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the mixed number 7 1/2 into its decimal equivalent, providing a detailed explanation suitable for learners of all levels. We'll cover various methods, delve into the underlying principles, and address frequently asked questions to ensure a complete understanding. This guide will equip you with the knowledge to confidently tackle similar conversions in the future.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion process, let's clarify the terms involved. A mixed number combines a whole number and a fraction, like 7 1/2. A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part (e.g., 7.5). The conversion process essentially involves expressing the fractional part of the mixed number as a decimal.
Method 1: Converting the Fraction to a Decimal
The most straightforward approach to converting 7 1/2 to a decimal involves focusing on the fractional component, 1/2. This fraction represents one part out of two equal parts. To convert this to a decimal, we perform a simple division:
1 ÷ 2 = 0.5
Therefore, the fraction 1/2 is equivalent to the decimal 0.5. Since our original mixed number is 7 1/2, we simply combine the whole number part (7) with the decimal equivalent of the fraction (0.5) to obtain the final answer:
7 + 0.5 = 7.5
Thus, 7 1/2 as a decimal is 7.5.
Method 2: Converting to an Improper Fraction
Another method involves first converting the mixed number 7 1/2 into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. To do this:
- Multiply the whole number (7) by the denominator of the fraction (2): 7 * 2 = 14
- Add the numerator of the fraction (1) to the result: 14 + 1 = 15
- Keep the same denominator (2): This gives us the improper fraction 15/2
Now, we convert the improper fraction 15/2 to a decimal by performing the division:
15 ÷ 2 = 7.5
Again, we arrive at the decimal equivalent of 7.5. This method highlights the interconnectedness between mixed numbers, improper fractions, and decimals.
Method 3: Using the Place Value System
Understanding the place value system is crucial for comprehending decimals. Each position to the right of the decimal point represents a decreasing power of 10. The first position is tenths (1/10), the second is hundredths (1/100), and so on.
In the case of 7 1/2, the fraction 1/2 represents one-half, or five-tenths (5/10). Therefore, we can directly write this as 0.5, and combining it with the whole number 7 gives us 7.5. This method emphasizes the direct relationship between fractions and their decimal representation.
Understanding the Concept of Halves
The number 7 1/2 holds a special significance as it directly represents half a unit. The fraction 1/2, or 0.5 in decimal form, is widely used and easily understood. Many everyday situations involve halves – splitting something in two, measuring half a cup of flour, or expressing a score of 7.5 out of 10. Understanding this intuitive concept strengthens your grasp of fractions and decimals.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in various contexts:
- Finance: Calculating percentages, interest rates, and proportions in financial transactions.
- Measurement: Converting measurements expressed as fractions (e.g., inches, centimeters) into decimals for greater accuracy and ease of calculation.
- Science: Representing scientific data and measurements precisely. Many scientific calculations require the use of decimal numbers.
- Everyday life: Dividing quantities fairly, calculating discounts, and understanding proportions in cooking recipes.
- Computer programming: Many programming languages and applications utilize decimal representation for numbers.
Mastering this skill provides a significant advantage in various aspects of life.
Expanding on Decimal Representation: Beyond Tenths
While 7 1/2 conveniently converts to a decimal with only one digit after the decimal point (7.5), it's important to remember that many fractions result in recurring or non-terminating decimals. For example, 1/3 converts to 0.333... (a recurring decimal), whereas the square root of 2 (approximately 1.414) is an example of a non-terminating decimal. Understanding the differences between these types of decimals expands your mathematical understanding.
Visual Representation of 7.5
Imagine a number line. The whole numbers are evenly spaced: 7, 8, 9, and so on. The point 7.5 lies exactly halfway between 7 and 8, perfectly illustrating its position as a value representing seven and a half units. This visual representation helps to solidify the understanding of the decimal value and its relationship to the whole numbers.
Frequently Asked Questions (FAQ)
Q1: Is there any other way to represent 7 1/2 as a decimal?
A1: No, 7.5 is the only precise decimal representation of 7 1/2. While you could express it as 7.50, 7.500, and so on (adding trailing zeros), these are essentially the same value.
Q2: What if I have a more complex fraction to convert?
A2: For more complex fractions, the method of converting to an improper fraction and then performing division always works. Alternatively, you can use a calculator.
Q3: Can all fractions be converted to terminating decimals?
A3: No. Fractions with denominators that have prime factors other than 2 and 5 will result in recurring or non-terminating decimals.
Q4: Why is understanding decimal representation important?
A4: Decimal representation is crucial for calculations, measurements, and data representation in various fields, making it a fundamental skill in mathematics and its applications.
Q5: How can I practice converting fractions to decimals?
A5: Practice regularly with various fractions, starting with simple ones and gradually increasing the complexity. Use online resources, textbooks, and worksheets to test your skills.
Conclusion
Converting 7 1/2 to a decimal, resulting in 7.5, is a simple yet fundamental concept that forms the basis for many more advanced mathematical operations. By understanding the different methods, grasping the underlying principles, and practicing regularly, you can confidently convert fractions to decimals and apply this skill in various real-world scenarios. Remember that the core of this conversion lies in comprehending the relationship between fractions and their decimal equivalents – a foundation for your continued mathematical journey. The ability to navigate these conversions smoothly contributes significantly to a broader understanding of numbers and their various representations.
Latest Posts
Latest Posts
-
1 14 As A Percent
Sep 15, 2025
-
18 Cm To Inches Conversion
Sep 15, 2025
-
43560 Square Feet To Miles
Sep 15, 2025
-
Converting Decimals Into Mixed Numbers
Sep 15, 2025
-
5 Divided By 1 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 7 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.