8 16 In Simplest Form
saludintensiva
Sep 16, 2025 · 5 min read
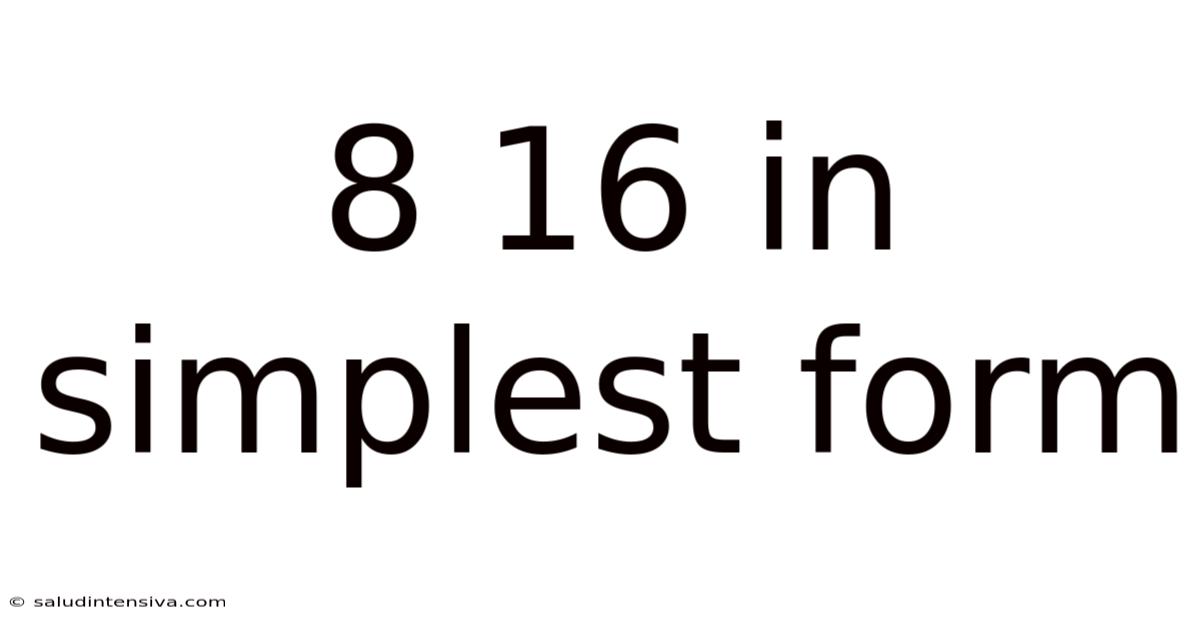
Table of Contents
Understanding Fractions: Simplifying 8/16 to its Simplest Form
Fractions are a fundamental concept in mathematics, representing parts of a whole. Understanding how to simplify fractions is crucial for various mathematical operations and real-world applications. This article will guide you through the process of simplifying the fraction 8/16, explaining the underlying principles and providing examples to solidify your understanding. We'll delve into the concept of greatest common divisors (GCD), explore different simplification methods, and even look at how this applies to real-world scenarios. By the end, you'll be able to confidently simplify fractions and apply this knowledge to more complex mathematical problems.
What is a Fraction?
Before we dive into simplifying 8/16, let's refresh our understanding of what a fraction represents. A fraction is written as a/b, where 'a' is the numerator (the top number) and 'b' is the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 8/16, the denominator 16 tells us the whole is divided into 16 equal parts, and the numerator 8 tells us we are considering 8 of those parts.
Simplifying Fractions: The Concept of Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This process involves finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To simplify 8/16, we need to find the GCD of 8 and 16. There are several ways to do this:
-
Listing Factors: List all the factors of 8 (1, 2, 4, 8) and all the factors of 16 (1, 2, 4, 8, 16). The largest number that appears in both lists is 8. Therefore, the GCD of 8 and 16 is 8.
-
Prime Factorization: Break down both numbers into their prime factors. The prime factorization of 8 is 2 x 2 x 2 (2³), and the prime factorization of 16 is 2 x 2 x 2 x 2 (2⁴). The common prime factors are 2 x 2 x 2 (2³), which equals 8. Therefore, the GCD is 8.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD. Let's apply this to 8 and 16:
16 ÷ 8 = 2 with a remainder of 0. Since the remainder is 0, the GCD is the divisor, which is 8.
Steps to Simplify 8/16
Now that we know the GCD of 8 and 16 is 8, we can simplify the fraction:
-
Divide the Numerator by the GCD: Divide the numerator (8) by the GCD (8): 8 ÷ 8 = 1
-
Divide the Denominator by the GCD: Divide the denominator (16) by the GCD (8): 16 ÷ 8 = 2
-
Write the Simplified Fraction: The simplified fraction is 1/2.
Therefore, 8/16 simplified to its simplest form is 1/2.
Visual Representation
Imagine you have a pizza cut into 16 slices. The fraction 8/16 represents having 8 out of 16 slices. If you group the slices into pairs (each pair representing 1/8 of the pizza), you will have 4 pairs. This demonstrates that 8/16 is equivalent to 4/8. Further grouping the pairs into larger groups of four slices will show that 4/8 is equivalent to 2/4 and finally to 1/2, visually confirming the simplification.
Further Examples of Fraction Simplification
Let's practice simplifying a few more fractions to reinforce the concept:
-
12/18: The GCD of 12 and 18 is 6. 12 ÷ 6 = 2 and 18 ÷ 6 = 3. Therefore, 12/18 simplifies to 2/3.
-
24/36: The GCD of 24 and 36 is 12. 24 ÷ 12 = 2 and 36 ÷ 12 = 3. Therefore, 24/36 simplifies to 2/3.
-
15/25: The GCD of 15 and 25 is 5. 15 ÷ 5 = 3 and 25 ÷ 5 = 5. Therefore, 15/25 simplifies to 3/5.
Real-World Applications of Fraction Simplification
Simplifying fractions isn't just an abstract mathematical exercise; it has many practical applications:
-
Cooking and Baking: Recipes often use fractions. Simplifying fractions helps in understanding and adjusting ingredient quantities. For example, if a recipe calls for 8/16 of a cup of sugar, knowing it's equivalent to 1/2 a cup makes measuring easier.
-
Measurements: In construction, engineering, or any field involving measurements, simplifying fractions helps in accurate calculations and conversions.
-
Data Analysis: When dealing with proportions or percentages, simplifying fractions makes the data easier to understand and interpret.
Frequently Asked Questions (FAQ)
-
What if the GCD is 1? If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. It cannot be simplified further.
-
Can I simplify a fraction by dividing the numerator and denominator by any common factor? Yes, you can, but it's more efficient to divide by the greatest common factor. Dividing by smaller common factors might require multiple steps to reach the simplest form.
-
What if the numerator is larger than the denominator? This is called an improper fraction. You can simplify an improper fraction in the same way as a proper fraction (where the numerator is smaller than the denominator). You can also convert an improper fraction to a mixed number (a whole number and a fraction).
-
Are there any shortcuts for finding the GCD? For relatively small numbers, listing factors or using prime factorization is often quickest. For larger numbers, the Euclidean algorithm is generally more efficient.
Conclusion
Simplifying fractions is a fundamental skill in mathematics. Understanding the concept of the greatest common divisor (GCD) and mastering the simplification process is crucial for solving various mathematical problems and understanding real-world applications. By following the steps outlined in this article, you can confidently simplify any fraction and apply this essential mathematical skill to various contexts. Remember, practice makes perfect! The more you work with fractions, the more comfortable and efficient you'll become in simplifying them to their simplest forms. So, grab a pencil and paper, and start practicing! You've got this!
Latest Posts
Latest Posts
-
2 3 Is Equivalent To What
Sep 16, 2025
-
Fraction From Smallest To Biggest
Sep 16, 2025
-
Is 43 Prime Or Composite
Sep 16, 2025
-
26 Acres To Sq Ft
Sep 16, 2025
-
4 5 X 1 6
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 16 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.