Gcf Of 12 And 4
saludintensiva
Sep 23, 2025 · 6 min read
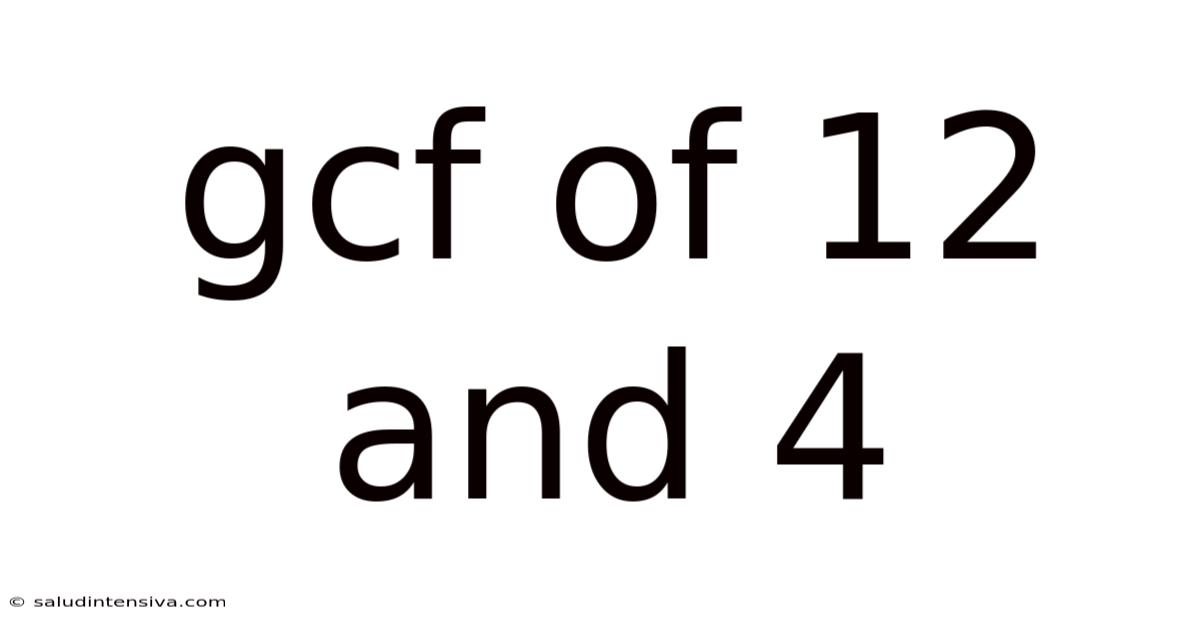
Table of Contents
Finding the Greatest Common Factor (GCF) of 12 and 4: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article will delve deep into finding the GCF of 12 and 4, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll move beyond simply stating the answer and instead illuminate the 'why' behind the calculations, making this concept accessible to learners of all levels.
Understanding Greatest Common Factor (GCF)
Before we jump into finding the GCF of 12 and 4, let's establish a clear understanding of what the GCF actually represents. The GCF of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. Think of it as the biggest number that is a factor of all the numbers in question. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 4 are 1, 2, and 4. The common factors shared by both 12 and 4 are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 12 and 4 is 4.
Method 1: Listing Factors
This is a straightforward method, particularly useful for smaller numbers like 12 and 4.
-
List the factors of each number:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 4: 1, 2, 4
-
Identify the common factors: The numbers appearing in both lists are the common factors. In this case, 1, 2, and 4 are common factors of 12 and 4.
-
Determine the greatest common factor: The largest number among the common factors is the GCF. Therefore, the GCF of 12 and 4 is 4.
This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers. Imagine trying to list all factors of 144 and 72! That's where more advanced methods come in handy.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This method is more robust and works well for larger numbers.
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3 (or 2² x 3)
- 4 = 2 x 2 (or 2²)
-
Identify common prime factors: Observe the prime factors of both 12 and 4. Both numbers share two factors of 2.
-
Calculate the GCF: Multiply the common prime factors together. In this case, 2 x 2 = 4. Therefore, the GCF of 12 and 4 is 4.
This method is particularly useful for understanding the fundamental structure of the numbers involved. It highlights the shared building blocks (prime factors) that contribute to the GCF.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. Let's illustrate with 12 and 4:
-
Divide the larger number by the smaller number and find the remainder: 12 ÷ 4 = 3 with a remainder of 0.
-
Interpret the remainder: If the remainder is 0, the smaller number is the GCF. In this case, the remainder is 0, so the GCF of 12 and 4 is 4.
If the remainder were not 0, we would continue the process by replacing the larger number with the smaller number and the smaller number with the remainder, then repeating step 1 until the remainder is 0. The last non-zero remainder would then be the GCF.
This method is elegant in its simplicity and efficiency, making it a preferred method for larger numbers where listing factors or prime factorization become cumbersome.
Visual Representation: Venn Diagram
A Venn diagram provides a visual representation of the factors and helps to understand the concept of common factors.
For 12 and 4:
- Circle 1 (12): 1, 2, 3, 4, 6, 12
- Circle 2 (4): 1, 2, 4
The overlapping section (the intersection) of the two circles contains the common factors: 1, 2, and 4. The largest number in this intersection is 4, which is the GCF.
Applications of GCF
The GCF finds application in numerous areas of mathematics and beyond:
-
Simplifying Fractions: To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, to simplify 12/4, we divide both by their GCF (4), resulting in 3/1 or simply 3.
-
Solving Equations: The GCF plays a role in solving equations involving polynomials by factoring out the common factor.
-
Real-world Problems: GCF can be used to solve problems involving equal grouping, such as dividing a collection of items into equal groups of maximum size. Imagine having 12 apples and 4 oranges, and you want to divide them into the largest possible equal groups. The GCF (4) indicates that you can create 4 equal groups, each containing 3 apples and 1 orange.
-
Geometry: GCF is useful in solving geometry problems related to area and volume calculations, often involving finding the dimensions of the largest square or cube that can fit within a larger shape.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For prime factorization, you would find the prime factorization of each number and then identify the common prime factors across all numbers. For the Euclidean algorithm, you would iteratively find the GCF of pairs of numbers until you arrive at the GCF of all the numbers.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the GCF of two numbers be larger than the smaller number?
- A: No. The GCF can never be larger than the smallest of the two numbers.
-
Q: Is there a limit to the size of numbers for which we can find the GCF?
- A: Theoretically, no. The Euclidean algorithm and prime factorization methods can be applied to numbers of any size, although the computational time might increase significantly for extremely large numbers. Specialized algorithms are used for exceptionally large numbers in computer science applications like cryptography.
-
Q: Why is understanding GCF important?
- A: Understanding GCF is crucial for a strong foundation in mathematics. It's a building block for more advanced concepts and has practical applications in various fields.
Conclusion
Finding the greatest common factor of two numbers, as demonstrated with the example of 12 and 4, is a fundamental skill in mathematics. We explored three methods: listing factors, prime factorization, and the Euclidean algorithm, highlighting their strengths and weaknesses. Understanding these methods provides a solid grasp of the underlying principles and allows for efficient calculation of the GCF, regardless of the size of the numbers involved. The applications of GCF extend beyond simple calculations, playing a significant role in various mathematical fields and real-world problem-solving. Mastering the concept of GCF is an essential step in building a strong mathematical foundation.
Latest Posts
Latest Posts
-
70 Percent As A Decimal
Sep 23, 2025
-
1 75 As A Percent
Sep 23, 2025
-
How High Is 20 Meters
Sep 23, 2025
-
8712 Sq Ft To Acres
Sep 23, 2025
-
7 15 As A Percent
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.