Gcf Of 3 And 27
saludintensiva
Sep 10, 2025 · 6 min read
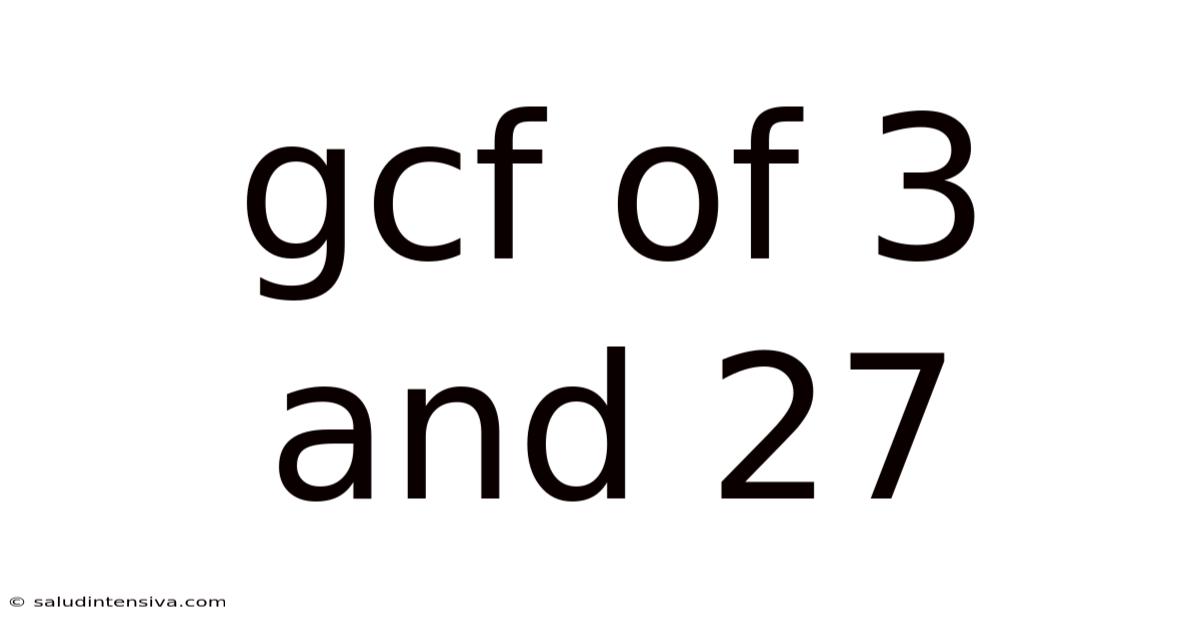
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 3 and 27: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with wide-ranging applications in mathematics and computer science. This article will explore the GCF of 3 and 27 in detail, providing a comprehensive understanding of the process, various methods for calculating it, and its significance in broader mathematical contexts. We'll move beyond a simple answer and delve into the underlying principles, offering a robust foundation for anyone wanting to master this essential skill.
Introduction to Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and working with various mathematical structures.
Methods for Finding the GCF of 3 and 27
Several methods can be employed to find the GCF of 3 and 27. We'll explore the most common and effective techniques:
1. Listing Factors:
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 3: 1, 3
- Factors of 27: 1, 3, 9, 27
The common factors are 1 and 3. The largest common factor is 3.
2. Prime Factorization:
This method is particularly useful for larger numbers. It involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 27: 3 x 3 x 3 = 3³
Both numbers share one 3 as a common prime factor. Therefore, the GCF is 3.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 3 and 27:
- Divide the larger number (27) by the smaller number (3): 27 ÷ 3 = 9 with a remainder of 0.
- Since the remainder is 0, the smaller number (3) is the GCF.
Therefore, the GCF of 3 and 27 is 3.
A Deeper Look at the Relationship Between 3 and 27
The fact that the GCF of 3 and 27 is 3 reveals a significant relationship between these two numbers. 27 is a multiple of 3 (27 = 3 x 9). This means 3 is a divisor of 27. This relationship is fundamental in understanding divisibility rules and factor relationships within the number system.
Applications of GCF in Real-World Scenarios
The concept of GCF extends beyond theoretical mathematics and finds practical applications in various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 27/3 can be simplified to 9/1 (or simply 9) by dividing both the numerator and denominator by their GCF, which is 3.
-
Geometry: GCF plays a role in solving geometric problems involving area and volume calculations, particularly when dealing with dimensions that need to be reduced to their simplest form.
-
Measurement and Units: When converting units of measurement, GCF helps simplify the calculations and express the results in the most concise form.
-
Computer Science: GCF algorithms are used in various computer science applications, including cryptography and data compression techniques. The efficiency of these algorithms is crucial for optimizing performance in computational tasks.
Expanding the Concept: GCF of More Than Two Numbers
The concept of GCF can be extended to more than two numbers. To find the GCF of multiple numbers, one can use the prime factorization method or the Euclidean algorithm (extended to handle multiple numbers). For instance, to find the GCF of 3, 27, and 9:
- Prime Factorization:
- 3 = 3¹
- 27 = 3³
- 9 = 3²
The common prime factor is 3, and the lowest power is 3¹. Therefore, the GCF of 3, 27, and 9 is 3.
- Euclidean Algorithm (extended): The Euclidean algorithm can be extended to find the GCF of multiple numbers by iteratively finding the GCF of pairs of numbers.
Least Common Multiple (LCM) and its Relationship to GCF
Closely related to the GCF is the least common multiple (LCM). The LCM of two or more integers is the smallest positive integer that is a multiple of each of the integers. The GCF and LCM are connected by a crucial relationship:
For any two positive integers a and b, the product of their GCF and LCM is equal to the product of the two numbers:
GCF(a, b) * LCM(a, b) = a * b
Using this relationship, we can find the LCM of 3 and 27:
GCF(3, 27) = 3 3 * LCM(3, 27) = 3 * 27 LCM(3, 27) = (3 * 27) / 3 = 27
This relationship provides an alternative way to calculate either the GCF or LCM if one of them is already known.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
A1: The GCF is the largest number that divides both numbers without a remainder, while the LCM is the smallest number that both numbers divide into without a remainder.
Q2: Can the GCF of two numbers be 1?
A2: Yes, if two numbers are relatively prime (meaning they share no common factors other than 1), their GCF is 1. For example, the GCF of 4 and 9 is 1.
Q3: Is there a limit to how many times the Euclidean algorithm needs to be applied?
A3: The Euclidean algorithm will always terminate in a finite number of steps, guaranteeing you will find the GCF. The number of steps depends on the initial numbers' relative sizes and the prime factorization of the numbers.
Q4: How can I use GCF to simplify a fraction?
A4: Divide both the numerator and denominator of the fraction by their GCF. This will reduce the fraction to its simplest form. For example, to simplify 27/9, find the GCF of 27 and 9 (which is 9), then divide both by 9 to get 3/1 or 3.
Conclusion: Mastering GCF and its Significance
Understanding the greatest common factor is essential for a strong foundation in mathematics. The methods outlined – listing factors, prime factorization, and the Euclidean algorithm – provide versatile approaches to finding the GCF. Beyond the simple calculation of the GCF of 3 and 27, this exploration highlights the deeper connections between numbers, illustrating their relationships and applications in various mathematical and real-world contexts. By mastering this fundamental concept, you open doors to a more profound understanding of number theory and its vast applications. The seemingly simple act of finding the GCF of 3 and 27 serves as a gateway to exploring more complex mathematical ideas, solidifying your numerical literacy and problem-solving skills.
Latest Posts
Latest Posts
-
5 Root 3 Whole Square
Sep 10, 2025
-
5 1 2 As A Decimal
Sep 10, 2025
-
11 2 As A Mixed Number
Sep 10, 2025
-
11 10 As A Decimal
Sep 10, 2025
-
Convert 98 Pounds To Kg
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 3 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.