Gcf Of 6 And 4
saludintensiva
Sep 12, 2025 · 6 min read
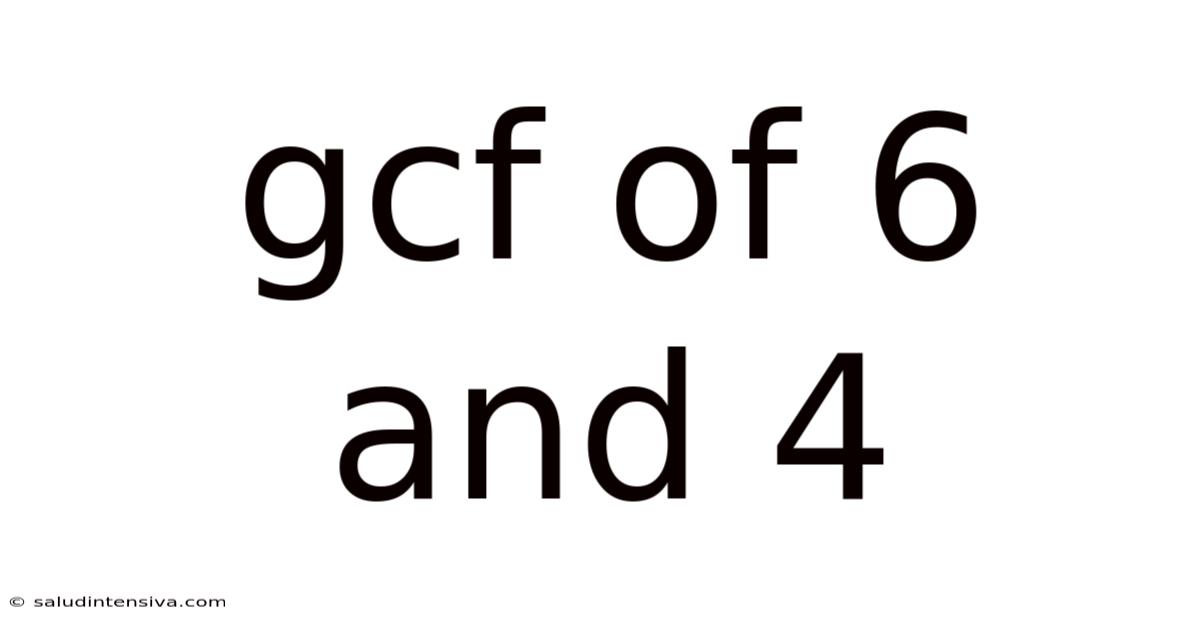
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 6 and 4: A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with far-reaching applications in mathematics and beyond. This article will delve into the GCF of 6 and 4, exploring various methods to determine it, explaining the underlying mathematical principles, and demonstrating its relevance in practical scenarios. We'll go beyond a simple answer and uncover the richness of this seemingly basic concept.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and even in more advanced areas like cryptography. This article will focus on finding the GCF of 6 and 4, providing multiple approaches to illustrate the concept thoroughly.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common factor.
- Factors of 6: 1, 2, 3, 6
- Factors of 4: 1, 2, 4
By comparing the two lists, we see that the common factors are 1 and 2. The largest of these common factors is 2. Therefore, the GCF of 6 and 4 is 2.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). This method is particularly useful for larger numbers.
- Prime factorization of 6: 2 x 3
- Prime factorization of 4: 2 x 2
To find the GCF using prime factorization, we identify the common prime factors and multiply them together. Both 6 and 4 share one common prime factor: 2. Therefore, the GCF of 6 and 4 is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to find the GCF of 6 and 4:
- Step 1: Since 6 > 4, we subtract 4 from 6: 6 - 4 = 2
- Step 2: Now we have the numbers 4 and 2. Since 4 > 2, we subtract 2 from 4: 4 - 2 = 2
- Step 3: We now have the numbers 2 and 2. Since they are equal, the GCF is 2.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, especially for larger numbers where listing factors might become cumbersome.
Understanding the Mathematical Significance of GCF
The GCF is not just a simple arithmetic operation; it holds significant importance in various mathematical contexts:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 6/4 can be simplified by dividing both the numerator and denominator by their GCF (2), resulting in the equivalent fraction 3/2.
-
Solving Equations: GCF plays a role in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Modular Arithmetic: The concept of GCF is fundamental in modular arithmetic, a branch of number theory used in cryptography and computer science.
-
Number Theory: GCF is a cornerstone of many number theory theorems and proofs. It's intrinsically linked to the concept of least common multiple (LCM), where GCF(a, b) * LCM(a, b) = a * b.
-
Real-world Applications: Beyond pure mathematics, GCF finds applications in various practical scenarios, such as dividing objects into equal groups, arranging items in arrays, or optimizing resource allocation.
Beyond the Basics: Exploring LCM and the Relationship with GCF
While this article focuses on the GCF, it's crucial to understand its relationship with the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. For 6 and 4, the LCM is 12. The relationship between GCF and LCM is given by the following formula:
GCF(a, b) * LCM(a, b) = a * b
In our case, GCF(6, 4) * LCM(6, 4) = 2 * 12 = 24, and 6 * 4 = 24. This formula demonstrates the inherent connection between these two important concepts in number theory.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Is there a limit to the number of methods for finding the GCF?
- A: No, there isn't a single "best" method. The optimal approach depends on the size and complexity of the numbers involved. For small numbers, listing factors is easy. For larger numbers, the Euclidean algorithm is more efficient.
-
Q: How does the GCF relate to the concept of divisibility?
- A: The GCF is directly related to divisibility. It represents the largest number that divides both numbers without leaving a remainder.
-
Q: Can the GCF be greater than either of the two numbers?
- A: No, the GCF cannot be greater than either of the two numbers. It must be a factor of both.
-
Q: Are there any online calculators or tools to find the GCF?
- A: Yes, many online calculators and software programs can calculate the GCF of any two (or more) numbers quickly and easily. However, understanding the underlying methods is crucial for a deeper grasp of the concept.
Conclusion: The Enduring Importance of the GCF
Finding the greatest common factor of 6 and 4, while seemingly straightforward, opens the door to a deeper understanding of fundamental concepts in number theory. The various methods discussed – listing factors, prime factorization, and the Euclidean algorithm – provide different perspectives on this important mathematical concept. The GCF isn't just a calculation; it's a key building block for more advanced mathematical concepts and has practical implications across diverse fields. Mastering the GCF lays a strong foundation for further exploration in mathematics and related disciplines. Remember, the seemingly simple concepts often hold the most profound implications. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Feet Squared To Inches Squared
Sep 12, 2025
-
5 9 In Decimal Form
Sep 12, 2025
-
8 9 Divided By 4
Sep 12, 2025
-
What Is 2 10 Simplified
Sep 12, 2025
-
Is 7 16 Bigger Than 1 2
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 6 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.