Gcf Of 60 And 45
saludintensiva
Sep 18, 2025 · 6 min read
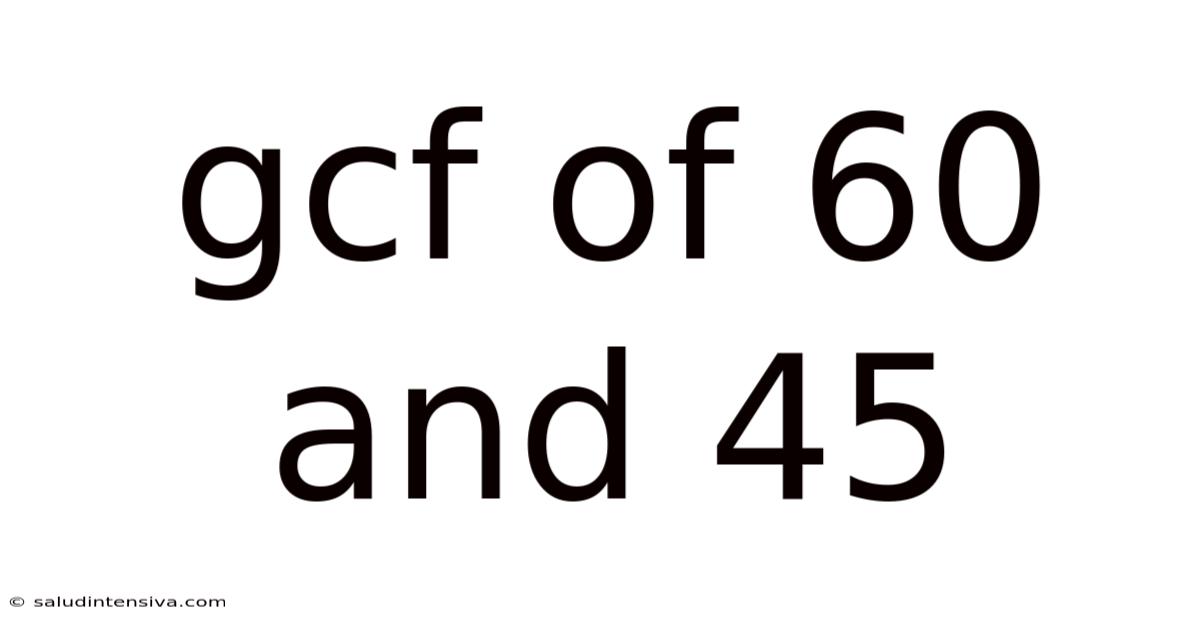
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 60 and 45: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex algebraic equations. This article will explore the GCF of 60 and 45 in detail, demonstrating various methods to calculate it and explaining the underlying mathematical principles. We'll delve beyond a simple answer, providing a comprehensive understanding of the concept and its significance.
Understanding Greatest Common Factor (GCF)
Before diving into the specific calculation for the GCF of 60 and 45, let's establish a clear understanding of what the GCF represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Understanding the GCF is crucial in various mathematical operations. It simplifies fractions to their lowest terms, aids in solving problems involving ratios and proportions, and plays a vital role in more advanced mathematical concepts like modular arithmetic and abstract algebra.
Method 1: Prime Factorization
The prime factorization method is a robust and widely used technique for determining the GCF of two or more numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of each number:
- 60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
- 45 = 3 x 3 x 5 = 3² x 5
-
Identify common prime factors: Both 60 and 45 share the prime factors 3 and 5.
-
Find the lowest power of each common prime factor: The lowest power of 3 is 3¹ (or simply 3), and the lowest power of 5 is 5¹.
-
Multiply the lowest powers of the common prime factors: 3 x 5 = 15
Therefore, the GCF of 60 and 45 is 15. This means 15 is the largest number that divides both 60 and 45 without leaving a remainder.
Method 2: Euclidean Algorithm
The Euclidean algorithm offers an efficient method for finding the GCF, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number represents the GCF.
Steps:
-
Start with the two numbers: 60 and 45.
-
Divide the larger number by the smaller number and find the remainder:
- 60 ÷ 45 = 1 with a remainder of 15
-
Replace the larger number with the smaller number, and the smaller number with the remainder: The new numbers are 45 and 15.
-
Repeat step 2:
- 45 ÷ 15 = 3 with a remainder of 0
-
When the remainder is 0, the GCF is the last non-zero remainder: In this case, the last non-zero remainder was 15.
Therefore, using the Euclidean algorithm, we again find that the GCF of 60 and 45 is 15.
Method 3: Listing Factors
This method involves listing all the factors of each number and identifying the largest common factor. While straightforward for smaller numbers, it becomes less efficient with larger numbers.
Steps:
-
List all the factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
-
List all the factors of 45: 1, 3, 5, 9, 15, 45
-
Identify the common factors: 1, 3, 5, 15
-
The largest common factor is the GCF: 15
This method confirms, once again, that the GCF of 60 and 45 is 15.
Illustrative Examples: Applications of GCF
The concept of GCF has numerous practical applications beyond simple mathematical exercises. Let's explore some examples:
-
Simplifying Fractions: Consider the fraction 60/45. By finding the GCF (15), we can simplify the fraction to its lowest terms: 60/45 = (60 ÷ 15) / (45 ÷ 15) = 4/3.
-
Dividing Objects Equally: Imagine you have 60 apples and 45 oranges. You want to divide them into identical bags, with each bag containing the same number of apples and oranges, and using all the fruit. To find the maximum number of bags you can make, you need to find the GCF of 60 and 45, which is 15. You can make 15 bags, each containing 4 apples and 3 oranges.
-
Ratio and Proportion: If the ratio of boys to girls in a class is 60:45, simplifying this ratio using the GCF (15) gives us a simplified ratio of 4:3. This makes it easier to understand and work with the ratio.
-
Geometry: The GCF can be used to find the dimensions of the largest square tile that can perfectly cover a rectangular area. If the rectangle measures 60 units by 45 units, the largest square tile would have sides of 15 units (the GCF of 60 and 45).
Beyond the Basics: Exploring Further Concepts
While we've focused on finding the GCF of two numbers, the concept extends to finding the GCF of more than two numbers. The methods described above, particularly prime factorization and the Euclidean algorithm, can be adapted to handle multiple numbers. For instance, to find the GCF of 60, 45, and 30, you would first find the prime factorization of each number and then identify the common prime factors with their lowest powers.
The GCF is also intrinsically linked to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. This relationship provides a valuable shortcut in certain calculations.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they have no common factors other than 1.
Q: Can the Euclidean algorithm be used for more than two numbers?
A: Yes, but you would apply the algorithm iteratively. First find the GCF of two numbers, then find the GCF of the result and the third number, and so on.
Q: Is there a formula to calculate the GCF?
A: There isn't a single formula that directly calculates the GCF for all cases. However, the relationships between the GCF, LCM, and the numbers themselves (as mentioned above) can be used to derive formulas in specific situations.
Q: Why is understanding GCF important?
A: Understanding GCF is fundamental to simplifying mathematical expressions, solving various types of problems, and building a solid foundation for more advanced mathematical concepts.
Conclusion
Finding the greatest common factor of 60 and 45, which we've determined to be 15, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory with far-reaching applications in various mathematical fields and real-world scenarios. By mastering different methods for calculating the GCF, such as prime factorization and the Euclidean algorithm, you equip yourself with powerful tools for simplifying complex mathematical problems and gaining a deeper appreciation for the elegance and interconnectedness of mathematical principles. The journey of understanding GCF is a stepping stone towards a richer appreciation of mathematics as a whole.
Latest Posts
Latest Posts
-
0 48 Acres To Sq Ft
Sep 18, 2025
-
3 5 Is Equivalent To
Sep 18, 2025
-
1 24 As A Percentage
Sep 18, 2025
-
Time Zone Converter Excel Formula
Sep 18, 2025
-
29 6 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 60 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.