Is 1/4 Bigger Than 1/8
saludintensiva
Sep 17, 2025 · 5 min read
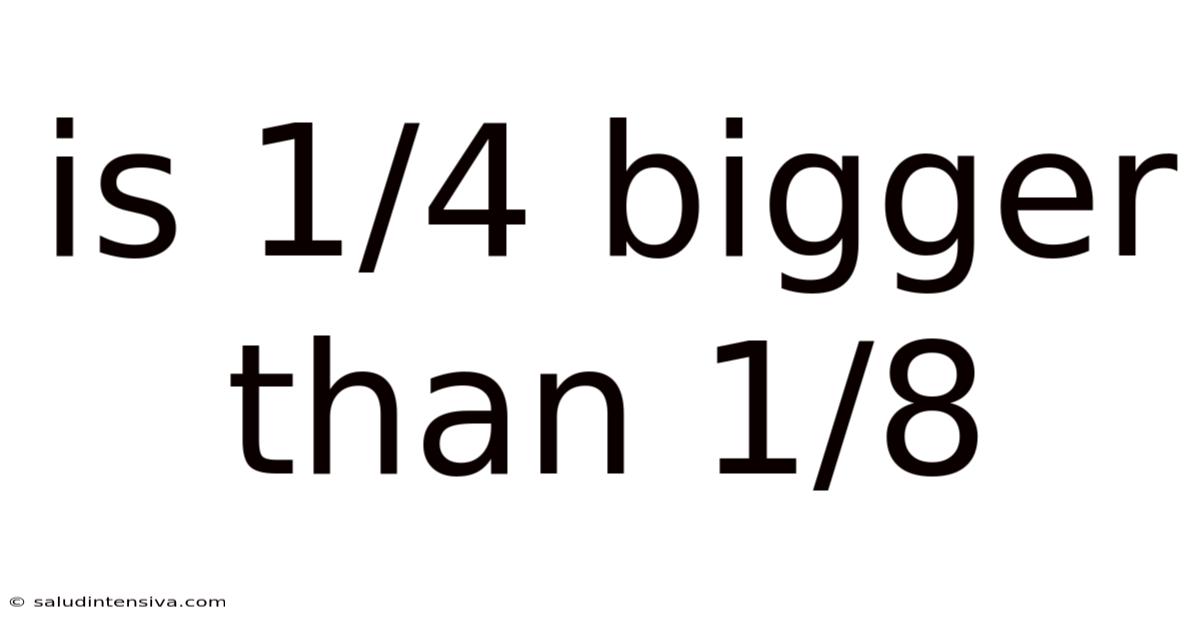
Table of Contents
Is 1/4 Bigger Than 1/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article tackles a seemingly simple question: is 1/4 bigger than 1/8? While the answer might seem obvious to some, we will explore this question in depth, covering various methods of comparison, offering explanations suitable for all learning levels, and delving into the underlying mathematical principles. This comprehensive guide will empower you to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have. For instance, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (1) means we have one of those parts.
Comparing 1/4 and 1/8: Visual Representation
One of the easiest ways to compare fractions is through visual aids. Imagine a pizza.
- 1/4: If we cut the pizza into four equal slices, 1/4 represents one of those slices.
- 1/8: If we cut the same pizza into eight equal slices, 1/8 represents one of those smaller slices.
By looking at the visual representation, it becomes immediately apparent that one slice out of four (1/4) is larger than one slice out of eight (1/8). This simple visual comparison makes the answer clear: yes, 1/4 is bigger than 1/8.
Comparing 1/4 and 1/8: Numerical Methods
While visual aids are helpful, especially for beginners, we need robust numerical methods for comparing fractions, especially when dealing with more complex examples. Here are a few approaches:
1. Common Denominator Method:
This is a classic and reliable method. To compare fractions, we need to rewrite them with the same denominator (bottom number). The least common multiple (LCM) of the denominators is the ideal choice.
- The denominators are 4 and 8. The LCM of 4 and 8 is 8.
- We convert 1/4 to an equivalent fraction with a denominator of 8: We multiply both the numerator and the denominator by 2 (8/4 = 2). This gives us 2/8.
- Now we compare 2/8 and 1/8. Since 2 is greater than 1, 2/8 (which is equal to 1/4) is greater than 1/8.
2. Decimal Conversion Method:
Another effective method involves converting the fractions to decimals. We simply divide the numerator by the denominator.
- 1/4 = 0.25
- 1/8 = 0.125
Comparing the decimal values, it's clear that 0.25 is greater than 0.125, confirming that 1/4 is bigger than 1/8.
3. Cross-Multiplication Method:
This method is particularly useful when comparing two fractions directly without finding a common denominator.
- We cross-multiply the numerators and denominators:
- 1 (from 1/4) x 8 (from 1/8) = 8
- 4 (from 1/4) x 1 (from 1/8) = 4
- Compare the results: 8 > 4. Since the result of the cross-multiplication involving 1/4 is greater, 1/4 is greater than 1/8.
The Underlying Mathematical Principle: Fraction Size and Denominator
The comparison of 1/4 and 1/8 highlights an important principle: for fractions with the same numerator, the fraction with the smaller denominator represents a larger portion of the whole. The smaller the denominator, the fewer equal parts the whole is divided into, and therefore each part is larger. This principle applies consistently across fractions. For example, 1/2 is larger than 1/3, 1/5 is larger than 1/10, and so on.
Extending the Concept: Comparing Fractions with Different Numerators and Denominators
The methods discussed above can be applied to compare any two fractions, even those with different numerators and denominators. Let's consider an example: comparing 3/5 and 2/3.
Using the Common Denominator Method:
- The LCM of 5 and 3 is 15.
- Convert 3/5 to an equivalent fraction with a denominator of 15: (3 x 3) / (5 x 3) = 9/15
- Convert 2/3 to an equivalent fraction with a denominator of 15: (2 x 5) / (3 x 5) = 10/15
- Compare 9/15 and 10/15: 10/15 > 9/15. Therefore, 2/3 is greater than 3/5.
Using the Decimal Conversion Method:
- 3/5 = 0.6
- 2/3 ≈ 0.6667
Comparing the decimal values, we see that 2/3 is greater than 3/5.
Using the Cross-Multiplication Method:
- 3 x 3 = 9
- 5 x 2 = 10
- 10 > 9. Therefore, 2/3 is greater than 3/5.
Frequently Asked Questions (FAQ)
Q1: Why is a smaller denominator associated with a larger fraction (when the numerators are the same)?
A1: Because a smaller denominator indicates that the whole is divided into fewer pieces. Each piece, therefore, is larger.
Q2: Are there any situations where this rule doesn't apply?
A2: Yes, the rule only applies when comparing fractions with the same numerator. If the numerators are different, you need to use the methods described above (common denominator, decimal conversion, or cross-multiplication) to compare them accurately.
Q3: Is there a shortcut for comparing simple fractions?
A3: For very simple fractions, you can often visualize them (like the pizza example) or use your intuition. However, for accuracy and to build a strong mathematical foundation, it's crucial to learn and apply the standard methods.
Q4: How can I improve my understanding of fractions?
A4: Practice is key! Work through numerous examples using different comparison methods. Visual aids, online resources, and practice problems can significantly enhance your understanding.
Conclusion
The answer to the question "Is 1/4 bigger than 1/8?" is a resounding yes. Through visual representation, numerical methods such as finding a common denominator, decimal conversion, and cross-multiplication, we've established that 1/4 is indeed larger than 1/8. This exploration goes beyond a simple answer; it provides a comprehensive understanding of fraction comparison, equipping you with the knowledge and skills to tackle more complex fraction problems. Remember the key principle: for fractions with the same numerator, the smaller the denominator, the larger the fraction. Mastering this concept forms a solid foundation for further mathematical exploration. Continue practicing, and you'll soon find yourself confidently navigating the world of fractions!
Latest Posts
Latest Posts
-
4 4 5 As A Decimal
Sep 17, 2025
-
12 Out Of 16 Percentage
Sep 17, 2025
-
General Form To Standard Form
Sep 17, 2025
-
10 Out Of 16 Percentage
Sep 17, 2025
-
93 Degrees Fahrenheit To Celsius
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Bigger Than 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.