12 Out Of 16 Percentage
saludintensiva
Sep 17, 2025 · 6 min read
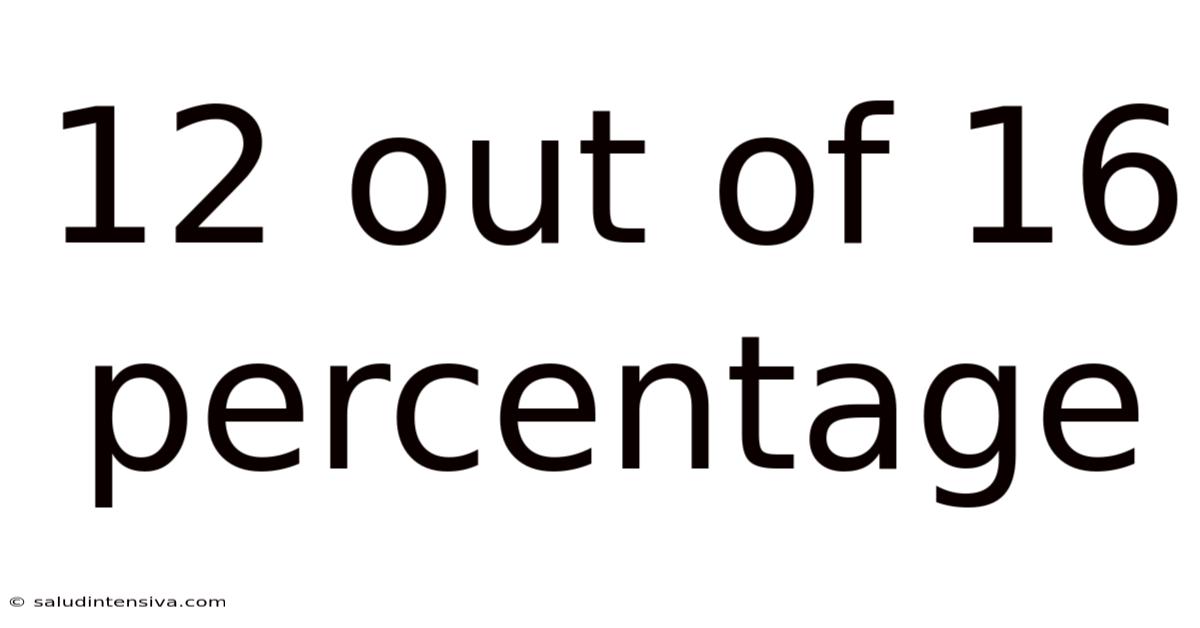
Table of Contents
Understanding 12 Out of 16: A Comprehensive Guide to Percentages and Ratios
Calculating percentages is a fundamental skill in various aspects of life, from academic assessments to financial management. Understanding how to express a portion as a percentage of a whole is crucial for interpreting data, making informed decisions, and communicating effectively. This article will delve into the calculation and interpretation of "12 out of 16," exploring the underlying principles of percentages and ratios, providing practical applications, and addressing frequently asked questions. This comprehensive guide aims to solidify your understanding of percentages and their significance in everyday contexts.
Introduction: What Does "12 out of 16" Mean?
The phrase "12 out of 16" represents a ratio or fraction. It signifies that 12 items or units are present out of a total of 16. This can be applied to various scenarios, such as exam scores (12 correct answers out of 16 questions), survey results (12 respondents out of 16 agreeing with a statement), or any situation involving a part-to-whole relationship. To fully understand this ratio, we need to translate it into a more readily interpretable form – a percentage.
Calculating the Percentage: From Ratio to Percentage
Converting a ratio or fraction to a percentage involves a straightforward process. The fundamental principle is to express the part (12) as a fraction of the whole (16), and then multiply by 100 to obtain the percentage:
-
Express as a fraction: 12/16
-
Simplify the fraction (optional but recommended): Both 12 and 16 are divisible by 4. Simplifying gives us 3/4.
-
Convert to decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Multiply by 100 to get the percentage: 0.75 x 100 = 75%
Therefore, 12 out of 16 represents 75%.
Understanding Percentages: The Bigger Picture
Percentages are a standardized way of expressing proportions. They offer a convenient and easily comparable method to represent fractions or ratios. A percentage always indicates a part of a whole, with the whole being represented by 100%. This universal scale allows for straightforward comparisons across different data sets. For example, understanding that 75% of students passed an exam is immediately more informative than knowing that 12 out of 16 students passed. The percentage provides context and ease of comparison.
Different Ways to Calculate Percentages
While the method above is the most common, there are other approaches to calculating percentages. These methods can be particularly useful depending on the context and available tools:
-
Using a calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 12 ÷ 16 x 100 = to get the result.
-
Using proportions: You can set up a proportion: 12/16 = x/100, where 'x' represents the percentage. Solving for 'x' will give you the percentage.
-
Using mental math (for simple fractions): Knowing common fraction-to-percentage conversions can be helpful for quick estimations. For example, recognizing that 3/4 is equivalent to 75% allows for immediate calculation without needing a calculator.
Practical Applications of Percentages: Real-World Examples
The concept of percentages finds widespread application in many areas of life. Here are some examples illustrating the relevance of understanding "12 out of 16" or similar percentage calculations:
-
Academic Performance: If a student answers 12 questions correctly out of 16 on a test, their score is 75%. This provides a clear representation of their performance.
-
Market Research: If 12 out of 16 respondents in a survey prefer a particular product, it indicates a 75% preference rate. This information is valuable for businesses in making informed decisions.
-
Financial Calculations: Understanding percentages is crucial for calculating interest rates, discounts, tax rates, and profit margins.
-
Data Analysis: Percentages are commonly used to represent proportions in statistical data, making it easier to interpret trends and draw conclusions.
-
Sports Statistics: Batting averages, field goal percentages, and free-throw percentages are all examples of using percentages to represent performance in sports.
Beyond the Calculation: Interpreting the Result
The calculation of 75% from "12 out of 16" is only half the story. The true value lies in interpreting this percentage within its context. Consider these points:
-
Significance of the context: A 75% score on a difficult exam might be considered excellent, while a 75% approval rating in a political poll might be considered moderate.
-
Comparison to benchmarks: Is 75% above or below average? Comparing the percentage to relevant benchmarks provides a more meaningful interpretation.
-
Potential sources of error: Were there any factors that might have influenced the result? Understanding limitations and potential biases in data collection is crucial.
Frequently Asked Questions (FAQ)
Q: What if I have a different ratio, such as 10 out of 16? How do I calculate the percentage?
A: Follow the same steps as outlined above. 10/16 simplifies to 5/8. 5 ÷ 8 = 0.625. 0.625 x 100 = 62.5%.
Q: Can percentages exceed 100%?
A: While percentages usually represent a part of a whole (less than or equal to 100%), there are instances where percentages can exceed 100%. This typically occurs when comparing a value to a base value that is less than the value being compared. For example, if sales this year are 150% of sales last year, it means this year's sales are 1.5 times the sales last year.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various examples, try different calculation methods, and apply percentages to real-world scenarios to build your confidence and understanding. Using online resources and practice exercises can also be beneficial.
Q: What are the differences between ratios, fractions, and percentages?
A: They are all ways to represent a part of a whole. A ratio compares two quantities, a fraction expresses a part of a whole as a numerator over a denominator, and a percentage expresses this fraction as a portion of 100. They are interconnected; a ratio can be expressed as a fraction, and a fraction can be expressed as a percentage.
Conclusion: Mastering Percentages for Everyday Success
Understanding "12 out of 16" and converting it to a percentage (75%) is not just about performing a calculation; it's about understanding the underlying concepts of ratios, fractions, and percentages. These skills are invaluable across various disciplines and are essential for interpreting data, making informed decisions, and communicating effectively. By grasping the fundamentals outlined in this guide, you can confidently navigate numerical challenges and apply percentage calculations to enhance your understanding of the world around you. The ability to convert ratios to percentages and interpret the results accurately will significantly improve your analytical skills and your capacity to make informed decisions in various aspects of life and work. Remember that practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
X 4 X 5 2
Sep 17, 2025
-
What Is Half Of 67
Sep 17, 2025
-
What Is 1 3 Of 1 5
Sep 17, 2025
-
2030 Military Time To Normal
Sep 17, 2025
-
3 5 As An Improper Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 16 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.