Is 1/4 Greater Than 5/8
saludintensiva
Sep 22, 2025 · 5 min read
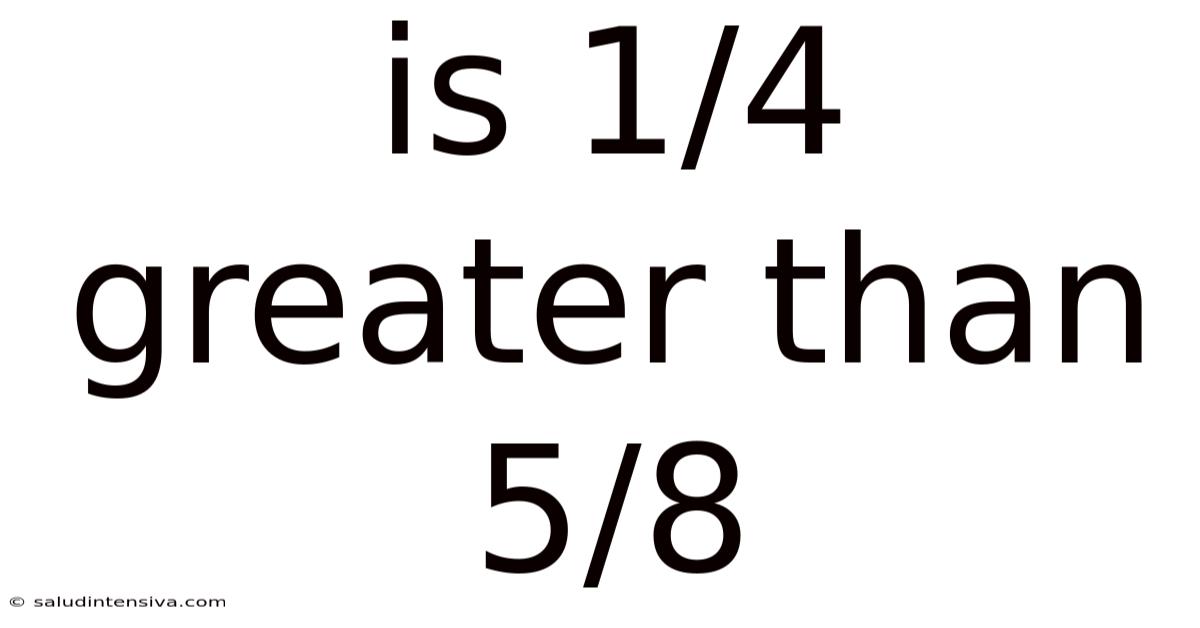
Table of Contents
Is 1/4 Greater Than 5/8? Understanding Fraction Comparison
This article will delve into the seemingly simple question: Is 1/4 greater than 5/8? While the answer might seem obvious to some, understanding the underlying principles of fraction comparison is crucial for building a strong foundation in mathematics. We'll explore different methods for comparing fractions, providing a detailed explanation accessible to all levels, from elementary school students to those looking for a refresher. This will include visual representations, numerical methods, and a discussion of the underlying mathematical concepts.
Understanding Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have. For example, in the fraction 1/4, the denominator (4) indicates the whole is divided into four equal parts, and the numerator (1) indicates we have one of those parts.
Method 1: Visual Representation
One of the easiest ways to compare fractions is to visualize them. We can represent 1/4 and 5/8 using diagrams.
Imagine a circle divided into four equal parts. Shading one part represents 1/4. Now, imagine another circle of the same size, but this time divided into eight equal parts. Shading five of those parts represents 5/8. By visually comparing the shaded areas, it becomes clear that 5/8 represents a larger portion of the whole than 1/4.
This visual method is particularly helpful for beginners, as it provides a concrete and intuitive understanding of fraction comparison.
Method 2: Finding a Common Denominator
A more formal method involves finding a common denominator for both fractions. A common denominator is a number that is a multiple of both denominators. In our case, the denominators are 4 and 8. Since 8 is a multiple of 4 (8 = 4 x 2), we can use 8 as our common denominator.
To convert 1/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2:
(1 x 2) / (4 x 2) = 2/8
Now we can compare 2/8 and 5/8. Since both fractions have the same denominator, we can simply compare their numerators. Since 2 < 5, we conclude that 2/8 < 5/8, and therefore, 1/4 < 5/8.
Method 3: Converting to Decimals
Another approach involves converting the fractions to decimals. To convert a fraction to a decimal, we divide the numerator by the denominator.
1/4 = 1 ÷ 4 = 0.25
5/8 = 5 ÷ 8 = 0.625
Comparing the decimal values, we see that 0.25 < 0.625, confirming that 1/4 is less than 5/8. This method is particularly useful when dealing with more complex fractions or when needing to perform further calculations.
Method 4: Cross-Multiplication
A less intuitive but efficient method is cross-multiplication. This involves multiplying the numerator of one fraction by the denominator of the other, and vice versa. We then compare the resulting products.
For 1/4 and 5/8:
1 x 8 = 8
5 x 4 = 20
Since 8 < 20, we conclude that 1/4 < 5/8. The fraction with the smaller product is the smaller fraction. This method works because it essentially finds a common numerator, implicitly.
The Importance of Equivalent Fractions
Throughout these methods, we've touched upon the concept of equivalent fractions. Equivalent fractions represent the same portion of a whole, even though they have different numerators and denominators. For example, 1/4, 2/8, and 4/16 are all equivalent fractions. Understanding equivalent fractions is essential for comparing and manipulating fractions effectively.
Addressing Potential Misconceptions
A common misconception is that a larger numerator automatically means a larger fraction. This is only true if the denominators are the same. When comparing fractions with different denominators, we must either find a common denominator, convert to decimals, or use cross-multiplication to make a valid comparison.
Further Exploration: Comparing More Complex Fractions
The methods described above can be applied to compare any two fractions, regardless of their complexity. For instance, to compare 7/12 and 2/3, we could find a common denominator (12), convert to decimals, or use cross-multiplication. The choice of method depends on personal preference and the context of the problem.
Practical Applications
The ability to compare fractions is a fundamental skill with wide-ranging applications in various fields:
- Cooking and Baking: Following recipes often requires understanding and comparing fractions to measure ingredients accurately.
- Construction and Engineering: Precise measurements and calculations in construction rely on accurate fraction comparison.
- Finance: Understanding fractions is crucial for managing budgets, calculating interest rates, and comprehending financial reports.
- Data Analysis: Many statistical analyses involve working with fractions and proportions.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to tell if one fraction is larger than another without doing calculations?
A: Not always. While visualizing simple fractions can provide a quick comparison, for more complex fractions, calculation is usually necessary to ensure accuracy.
Q: What if the fractions are mixed numbers (e.g., 1 1/2 and 2 1/4)?
A: Convert the mixed numbers into improper fractions before applying any of the comparison methods described above.
Q: Are there any online tools or calculators that can help compare fractions?
A: Yes, many online fraction calculators are available. However, understanding the underlying methods is crucial for developing mathematical skills and problem-solving abilities.
Conclusion
The answer to the question, "Is 1/4 greater than 5/8?" is a definitive no. 1/4 is less than 5/8. This seemingly simple comparison highlights the importance of understanding the fundamental principles of fraction comparison. By mastering the methods outlined in this article—visual representation, finding a common denominator, converting to decimals, and cross-multiplication—you'll build a solid foundation for tackling more complex mathematical problems and confidently navigating situations where fraction comparison is necessary. Remember, practice is key to mastering these concepts, so try comparing different fractions using various methods to reinforce your understanding.
Latest Posts
Latest Posts
-
98 6 F To C
Sep 22, 2025
-
What Is 3 4 In Inches
Sep 22, 2025
-
Is 2 3 More Than 1 4
Sep 22, 2025
-
60 Days From February 10
Sep 22, 2025
-
5 23 As A Percent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Greater Than 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.