Is 1/4 More Than 1/8
saludintensiva
Sep 13, 2025 · 5 min read
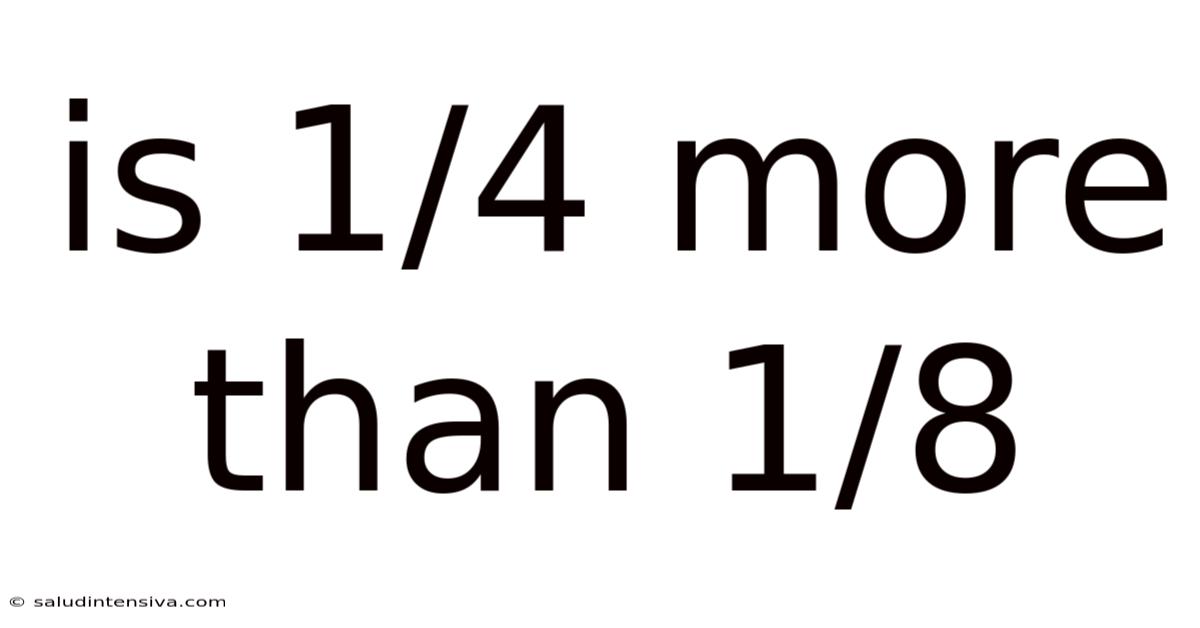
Table of Contents
Is 1/4 More Than 1/8? A Deep Dive into Fraction Comparison
Is 1/4 more than 1/8? The answer, at first glance, seems simple: yes. But understanding why 1/4 is greater than 1/8 requires a deeper understanding of fractions, their representation, and various methods for comparison. This article will not only answer this question definitively but also equip you with the tools to compare any two fractions with confidence. We'll explore visual representations, numerical methods, and even delve into the underlying mathematical principles. By the end, you'll be able to confidently tackle fraction comparisons and explain the concepts to others.
Understanding Fractions: A Quick Refresher
Before we dive into comparing 1/4 and 1/8, let's quickly review what a fraction represents. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells you how many equal parts the whole is divided into, and the numerator tells you how many of those parts you have.
For example, in the fraction 1/4, the denominator 4 indicates that the whole is divided into four equal parts. The numerator 1 indicates that we are considering one of those four parts. Similarly, in the fraction 1/8, the whole is divided into eight equal parts, and we're considering just one of them.
Visualizing the Comparison: The Power of Pictures
One of the easiest ways to compare fractions is to visualize them. Imagine a pizza.
- 1/4: If you cut the pizza into four equal slices, 1/4 represents one of those slices.
- 1/8: If you cut the same pizza into eight equal slices, 1/8 represents one of those smaller slices.
It's visually apparent that one-quarter slice (1/4) is larger than one-eighth slice (1/8). This visual representation provides an intuitive understanding of why 1/4 > 1/8.
Numerical Comparison: Finding a Common Denominator
While visual aids are helpful, a more robust method for comparing fractions involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. In this case, we're comparing 1/4 and 1/8. The least common multiple (LCM) of 4 and 8 is 8.
To convert 1/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2:
(1 × 2) / (4 × 2) = 2/8
Now we can easily compare 2/8 and 1/8. Since 2 is greater than 1, we conclude that 2/8 (which is equivalent to 1/4) is greater than 1/8.
Decimal Conversion: Another Approach
Another way to compare fractions is to convert them into decimals. To convert a fraction to a decimal, simply divide the numerator by the denominator:
- 1/4 = 1 ÷ 4 = 0.25
- 1/8 = 1 ÷ 8 = 0.125
Comparing the decimal values, 0.25 is clearly larger than 0.125, confirming that 1/4 > 1/8. This method is particularly useful when dealing with more complex fractions or when comparing fractions to decimals.
Understanding the Relationship: Proportional Reasoning
The relationship between 1/4 and 1/8 can also be understood through proportional reasoning. If we double the denominator of 1/4 (multiplying by 2), we get 1/8. However, to maintain the same proportion, we must also double the numerator. This results in 2/8, which is equivalent to 1/4. Since 2/8 > 1/8, we again confirm that 1/4 > 1/8. This method emphasizes the importance of equivalent fractions in comparison.
Beyond 1/4 and 1/8: Generalizing the Comparison Method
The techniques we've used to compare 1/4 and 1/8 are applicable to any two fractions. To compare two fractions, a/b and c/d:
- Find a common denominator: Find the least common multiple (LCM) of b and d.
- Convert to equivalent fractions: Convert both fractions to equivalent fractions with the common denominator found in step 1.
- Compare numerators: Compare the numerators of the equivalent fractions. The fraction with the larger numerator is the larger fraction.
Alternatively, you can convert both fractions to decimals and compare the decimal values.
Common Mistakes to Avoid
When comparing fractions, several common mistakes can lead to incorrect conclusions. Let's address some of these:
- Comparing numerators directly without considering denominators: This is a common error. Simply because the numerator of 1/8 is smaller than the numerator of 1/4 doesn't automatically mean the fraction is smaller. The denominator plays a crucial role.
- Incorrectly finding common denominators or equivalent fractions: Carefully follow the steps for finding the LCM and converting fractions to ensure accuracy.
- Misinterpreting decimal conversions: Round-off errors during decimal conversion can sometimes lead to inaccurate comparisons, especially with repeating decimals.
Frequently Asked Questions (FAQ)
Q: Can I always use the visual method to compare fractions?
A: The visual method is excellent for building intuition and understanding, but it's not always practical, especially when dealing with complex fractions or fractions with large denominators. Numerical methods are more reliable for accurate comparisons in such cases.
Q: What if the denominators are prime numbers?
A: If the denominators are prime numbers (like 2 and 7), the common denominator will simply be their product (in this case, 14). You would then convert each fraction to an equivalent fraction with a denominator of 14 and compare the numerators.
Q: What if I have mixed numbers?
A: Convert mixed numbers (like 1 1/2) to improper fractions (like 3/2) before applying the comparison methods outlined above.
Conclusion: Mastering Fraction Comparison
Understanding the relationship between fractions, especially comparing fractions like 1/4 and 1/8, is fundamental to mathematical literacy. This article has demonstrated various methods for comparing fractions, from visual representations to numerical techniques like finding common denominators and decimal conversions. By mastering these methods, you can confidently compare any two fractions and build a strong foundation in mathematical reasoning. Remember, the key is to understand the underlying principles – the meaning of the numerator and denominator and the importance of equivalent fractions. Practice regularly, and you'll soon become proficient in fraction comparison. With consistent effort, comparing fractions will become second nature, paving the way for tackling more complex mathematical concepts.
Latest Posts
Latest Posts
-
5 14 As A Percent
Sep 13, 2025
-
Factors Of 10 In Pairs
Sep 13, 2025
-
What Are The Factors 20
Sep 13, 2025
-
Lcm For 18 And 30
Sep 13, 2025
-
Ti 84 Graphing Calculator Online
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 More Than 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.