Is 2/6 Equivalent To 4/12
saludintensiva
Sep 17, 2025 · 7 min read
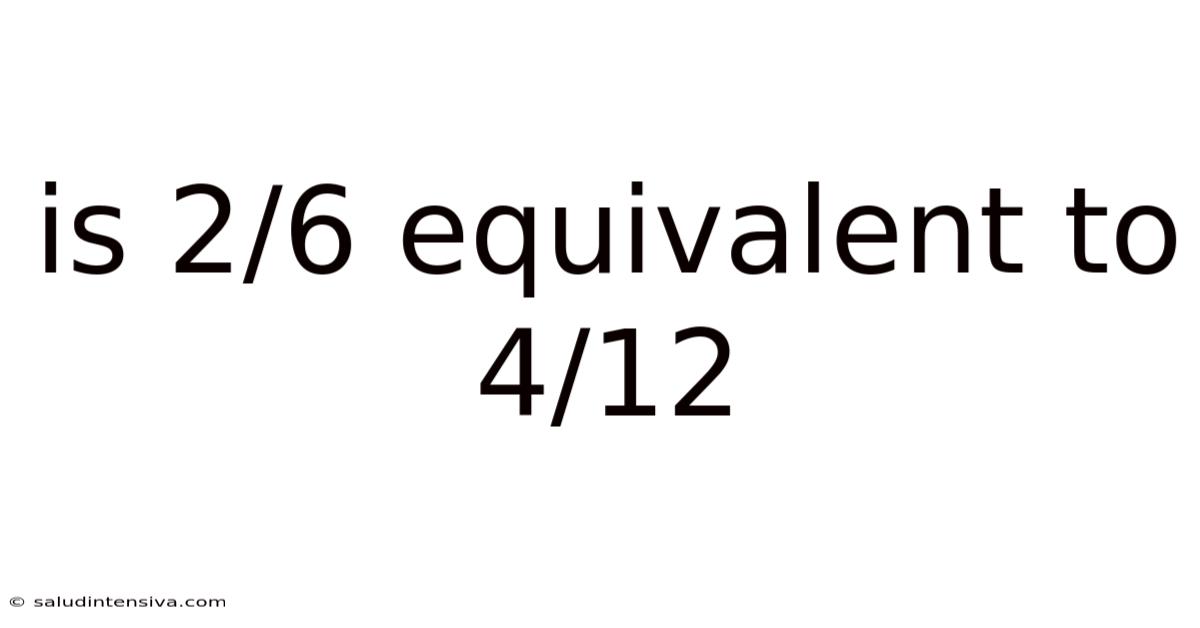
Table of Contents
Is 2/6 Equivalent to 4/12? A Deep Dive into Fraction Equivalence
Understanding fraction equivalence is a cornerstone of mathematical proficiency. It's a concept that builds a strong foundation for more advanced mathematical operations, including algebra, calculus, and even real-world applications like cooking and construction. This article explores the equivalence of 2/6 and 4/12, not just by confirming their equality, but by delving into the underlying principles and providing a comprehensive understanding of fraction equivalence for all levels of learners. We will explore various methods to determine equivalence, explain the underlying mathematical rationale, and address common misconceptions.
Introduction: The Fundamentals of Fractions
Before we dive into the specific case of 2/6 and 4/12, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/6, 2 is the numerator and 6 is the denominator. This means we have 2 parts out of a total of 6 equal parts.
Visualizing Fraction Equivalence: The Power of Representation
One of the most effective ways to understand fraction equivalence is through visual representations. Imagine a pizza cut into six equal slices. If you take two slices, you've taken 2/6 of the pizza. Now, imagine another pizza, this time cut into twelve equal slices. If you take four slices of this pizza, you've also taken 4/12 of the pizza. Both scenarios represent the same amount of pizza – one-third of the whole. This visual demonstration clearly illustrates that 2/6 and 4/12 are equivalent fractions.
Method 1: Simplifying Fractions to Their Lowest Terms
A fundamental approach to determining fraction equivalence involves simplifying fractions to their lowest terms. This means reducing the numerator and denominator to their smallest possible whole numbers while maintaining the same ratio. We achieve this by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's apply this to 2/6:
- Find the GCD of 2 and 6: The GCD of 2 and 6 is 2.
- Divide both the numerator and denominator by the GCD: 2 ÷ 2 = 1 and 6 ÷ 2 = 3.
- Simplified fraction: The simplified form of 2/6 is 1/3.
Now let's simplify 4/12:
- Find the GCD of 4 and 12: The GCD of 4 and 12 is 4.
- Divide both the numerator and denominator by the GCD: 4 ÷ 4 = 1 and 12 ÷ 4 = 3.
- Simplified fraction: The simplified form of 4/12 is 1/3.
Since both 2/6 and 4/12 simplify to 1/3, they are equivalent.
Method 2: Cross-Multiplication
Another method to verify fraction equivalence is through cross-multiplication. We multiply the numerator of one fraction by the denominator of the other and vice-versa. If the products are equal, the fractions are equivalent.
Let's test 2/6 and 4/12:
- Cross-multiply: (2 x 12) = 24 and (6 x 4) = 24.
- Result: Since the products are equal (24 = 24), the fractions 2/6 and 4/12 are equivalent.
This method provides a quick and efficient way to check for equivalence, particularly when dealing with larger numbers where simplification might be more time-consuming.
Method 3: Finding Equivalent Fractions by Multiplication
We can create equivalent fractions by multiplying both the numerator and the denominator by the same non-zero number. This process doesn't change the value of the fraction; it simply represents the same proportion using different numbers.
Let's start with 1/3:
- Multiply by 2: (1 x 2) / (3 x 2) = 2/6
- Multiply by 4: (1 x 4) / (3 x 4) = 4/12
This demonstrates that 1/3, 2/6, and 4/12 are all equivalent fractions. This approach clearly shows how multiple fractions can represent the same portion of a whole.
The Mathematical Rationale Behind Fraction Equivalence
The equivalence of fractions stems from the fundamental concept of proportionality. Two fractions are equivalent if they represent the same ratio or proportion. This means that the relationship between the numerator and the denominator remains constant even when the numbers change. Multiplying or dividing both the numerator and the denominator by the same non-zero number maintains this constant ratio. Therefore, any fraction obtained by multiplying or dividing both parts of a fraction by the same non-zero number will be equivalent to the original fraction.
Addressing Common Misconceptions
Several misconceptions often surround fraction equivalence. One common error is believing that adding the same number to both the numerator and the denominator creates an equivalent fraction. This is incorrect. For example, adding 1 to both the numerator and denominator of 1/2 results in 2/3, which is not equivalent to 1/2. Only multiplying or dividing both parts by the same non-zero number maintains equivalence.
Another misconception is assuming that fractions with larger numbers are always larger. This is also false. A fraction with a larger numerator and denominator doesn't automatically mean it's a larger value. The ratio between the numerator and the denominator determines the size of the fraction.
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is crucial in numerous real-world scenarios. Consider baking a cake: if a recipe calls for 2/6 cup of sugar, and you only have a 1/3 cup measuring cup, you know you can use that without altering the recipe's outcome. Similarly, in construction, accurately measuring materials often requires converting between equivalent fractions to ensure precise measurements. In finance, understanding equivalent fractions is vital for calculating proportions of investments, debts, and profits. In short, fraction equivalence is a fundamental skill with widespread practical application.
Frequently Asked Questions (FAQ)
Q1: Are all fractions with the same simplified form equivalent?
A1: Yes, all fractions that simplify to the same lowest terms are equivalent. They represent the same proportion or ratio.
Q2: Can I always simplify a fraction to its lowest terms?
A2: Yes, except for cases involving irrational numbers where the denominator might be an infinitely repeating decimal.
Q3: Is there a limit to the number of equivalent fractions for a given fraction?
A3: No, there are infinitely many equivalent fractions for any given fraction. You can always multiply the numerator and denominator by any non-zero integer to generate a new equivalent fraction.
Q4: How can I tell if two fractions are equivalent without simplifying or cross-multiplying?
A4: Visually comparing the fractions using area models or number lines can help determine equivalence. However, simplification and cross-multiplication provide more reliable methods for larger numbers.
Q5: Why is understanding fraction equivalence important?
A5: Understanding fraction equivalence is crucial for performing various mathematical operations, solving problems, and for numerous real-world applications across various fields. It's a foundational skill that underpins much of higher-level mathematics.
Conclusion: Mastering Fraction Equivalence
In conclusion, the fractions 2/6 and 4/12 are indeed equivalent. This equivalence stems from the fundamental principle of proportionality in fractions. We've explored multiple methods – simplification, cross-multiplication, and generating equivalent fractions – to demonstrate this equivalence. Mastering fraction equivalence is not merely about memorizing procedures; it's about understanding the underlying mathematical rationale and its far-reaching applications in various contexts. By grasping this concept thoroughly, students build a strong foundation for future mathematical success and develop essential problem-solving skills applicable to everyday life. The ability to recognize and work with equivalent fractions is a vital skill, a cornerstone of mathematical understanding and problem-solving, applicable across a range of disciplines and real-world scenarios.
Latest Posts
Latest Posts
-
27 To The Power Of
Sep 17, 2025
-
Whats Equivalent To 1 4
Sep 17, 2025
-
23 6 As A Mixed Number
Sep 17, 2025
-
7 8 As A Percentage
Sep 17, 2025
-
Whats 20 As A Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 2/6 Equivalent To 4/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.