Lcm Of 13 And 11
saludintensiva
Sep 15, 2025 · 6 min read
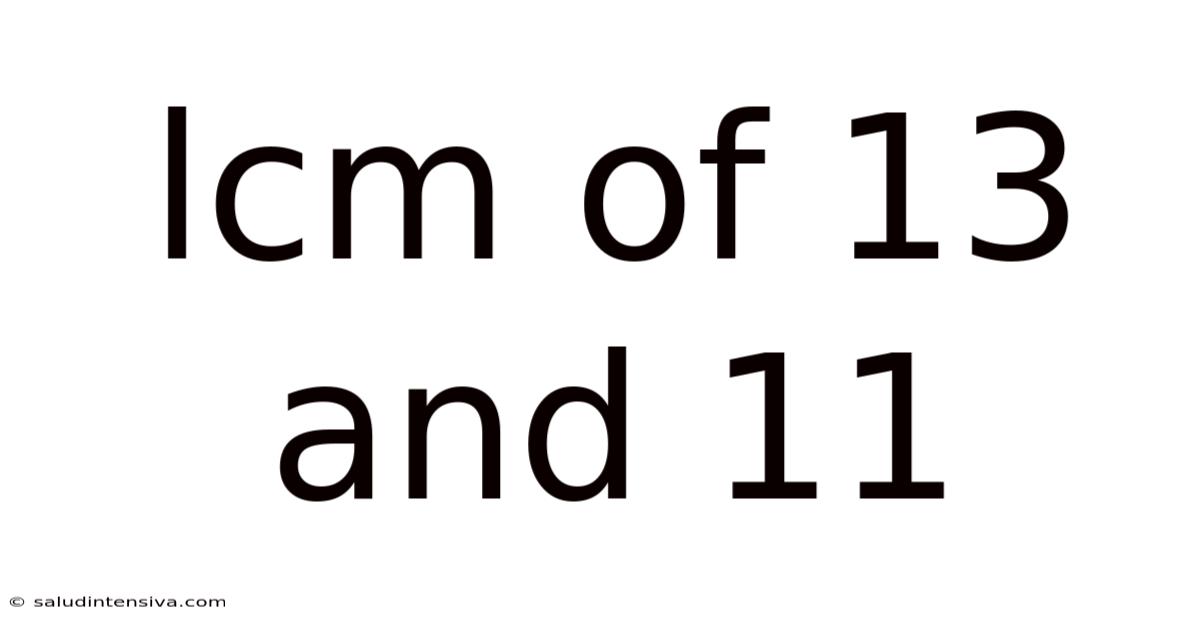
Table of Contents
Finding the Least Common Multiple (LCM) of 13 and 11: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, especially when dealing with relatively small numbers like 13 and 11. However, understanding the underlying principles behind LCM calculations opens the door to a fascinating world of number theory and its applications in various fields like computer science, cryptography, and music theory. This article will not only guide you through calculating the LCM of 13 and 11 but also delve deeper into the concepts, exploring different methods and their underlying mathematical reasoning. We'll also touch upon the relationship between LCM and the greatest common divisor (GCD), providing a comprehensive understanding of these fundamental concepts.
Introduction: Understanding LCM and its Significance
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. This concept is crucial in various mathematical operations and real-world applications. For instance, in scheduling problems, finding the LCM helps determine the next time two events will occur simultaneously. In music, LCM is used to find the least common denominator when dealing with different time signatures.
Method 1: Prime Factorization Method – Unveiling the Building Blocks
The most fundamental and widely used method for finding the LCM involves prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, 13). Prime factorization is the process of expressing a number as a product of its prime factors.
Let's find the LCM of 13 and 11 using this method:
-
Find the prime factorization of each number:
- 13 is a prime number itself, so its prime factorization is simply 13.
- 11 is also a prime number, so its prime factorization is 11.
-
Identify the highest power of each prime factor:
Both 13 and 11 appear only once in their respective factorizations. Therefore, the highest power of 13 is 13¹ and the highest power of 11 is 11¹.
-
Multiply the highest powers together:
LCM(13, 11) = 13¹ * 11¹ = 143
Therefore, the least common multiple of 13 and 11 is 143. This means that 143 is the smallest positive integer divisible by both 13 and 11.
Method 2: Listing Multiples – A More Intuitive Approach
This method involves listing the multiples of each number until a common multiple is found. While straightforward, it becomes less efficient when dealing with larger numbers.
-
List multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, ...
-
List multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, ...
-
Identify the smallest common multiple: The smallest number appearing in both lists is 143.
Therefore, the LCM(13, 11) = 143.
Method 3: Using the Formula Relating LCM and GCD – A Powerful Connection
The greatest common divisor (GCD) of two integers is the largest positive integer that divides both integers without leaving a remainder. There's a fundamental relationship between the LCM and GCD of two numbers:
- LCM(a, b) * GCD(a, b) = a * b
This formula provides an alternative way to calculate the LCM if the GCD is known.
-
Find the GCD of 13 and 11:
Since both 13 and 11 are prime numbers and have no common factors other than 1, their GCD is 1.
-
Apply the formula:
LCM(13, 11) = (13 * 11) / GCD(13, 11) = (13 * 11) / 1 = 143
This method confirms that the LCM of 13 and 11 is 143.
Exploring the Mathematical Underpinnings: Why does this work?
The effectiveness of these methods is rooted in fundamental principles of number theory. The prime factorization method works because it breaks down the numbers into their irreducible components, allowing us to construct the smallest number containing all these components. The relationship between LCM and GCD highlights the inherent structure and relationships within the number system. Every positive integer can be uniquely expressed as a product of primes (Fundamental Theorem of Arithmetic). This unique factorization underlies the success of the prime factorization method for finding the LCM.
Applications of LCM: Beyond the Classroom
The concept of LCM has far-reaching applications beyond the realm of pure mathematics:
-
Scheduling: Imagine two buses departing from the same station at different intervals. The LCM of their departure intervals determines when they will depart simultaneously again.
-
Music Theory: Musical rhythms and time signatures often involve fractional relationships. Finding the LCM helps in determining the smallest common denominator for harmonizing different rhythms.
-
Computer Science: LCM is used in various algorithms and data structures, particularly in tasks related to modular arithmetic and synchronization.
-
Construction and Engineering: In designing structures or systems, LCM might be used to optimize material usage or to find the smallest common length for components.
Frequently Asked Questions (FAQ)
-
Q: Is the LCM always greater than the numbers involved?
- A: Yes, except in the case where one number is a multiple of the other. For example, LCM(4, 8) = 8.
-
Q: Can I use the prime factorization method for finding the LCM of more than two numbers?
- A: Yes, absolutely. You would find the prime factorization of each number, identify the highest power of each prime factor present across all numbers, and then multiply these highest powers together.
-
Q: What if the numbers are very large?
- A: For very large numbers, using the Euclidean algorithm to find the GCD first, then employing the LCM-GCD relationship (LCM(a, b) * GCD(a, b) = a * b), becomes computationally more efficient than directly using prime factorization. Specialized algorithms exist to handle exceptionally large numbers effectively.
Conclusion: A Deeper Appreciation of Number Theory
Calculating the least common multiple of 13 and 11, while seemingly straightforward, provides a gateway to a deeper understanding of fundamental mathematical concepts. We've explored various methods – prime factorization, listing multiples, and the LCM-GCD relationship – each illustrating different facets of number theory. These methods are not only useful tools for solving mathematical problems but also demonstrate the underlying structure and elegance of the number system. Understanding LCM contributes to a richer appreciation of mathematics and its applications in diverse fields, highlighting the interconnectedness of mathematical concepts and their practical relevance in our world. The simplicity of calculating the LCM of 13 and 11 belies the depth and breadth of the underlying mathematical principles, emphasizing the power and beauty of number theory.
Latest Posts
Latest Posts
-
Convert 4 Into A Fraction
Sep 15, 2025
-
3 1 4 To Improper Fraction
Sep 15, 2025
-
Lcm Of 5 6 8
Sep 15, 2025
-
Convert 8 Into A Fraction
Sep 15, 2025
-
9 50 As A Percent
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 13 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.