Lcm Of 5 6 8
saludintensiva
Sep 15, 2025 · 6 min read
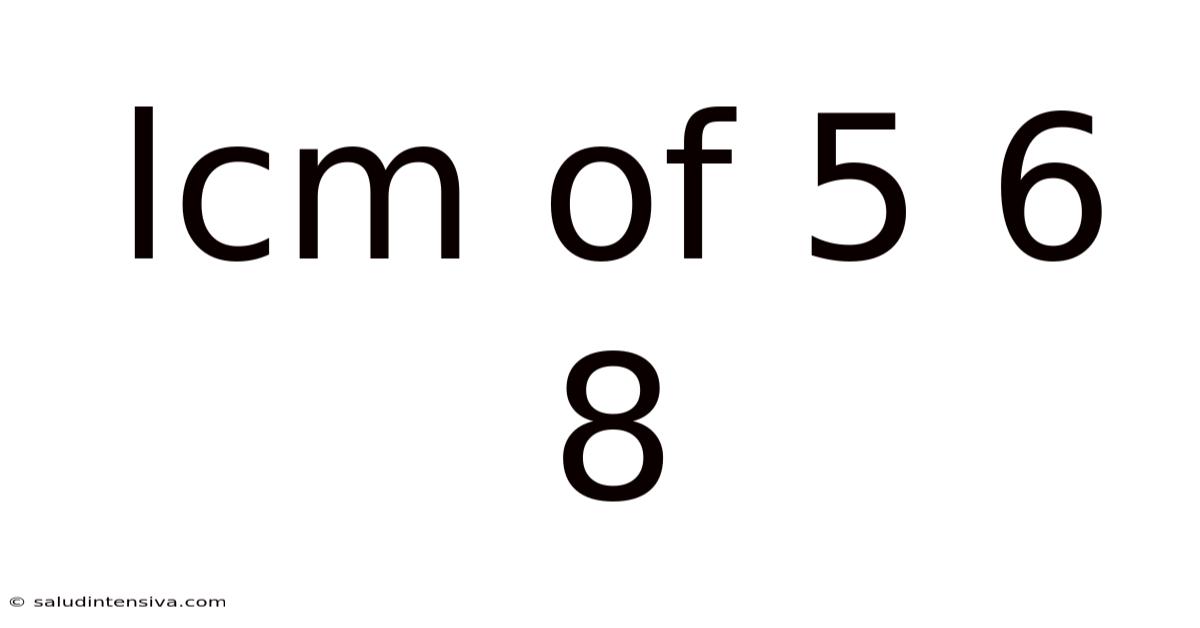
Table of Contents
Finding the Least Common Multiple (LCM) of 5, 6, and 8: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will walk you through the process of calculating the LCM of 5, 6, and 8, explaining different methods and providing a deeper understanding of the underlying principles. Understanding LCM is not just about memorizing formulas; it's about grasping the concept of multiples and their relationships. This article will help you achieve that.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 5, 6, and 8, let's establish a solid foundation. The least common multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. Multiples of 2 are: 2, 4, 6, 8, 10, 12... Multiples of 3 are: 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 96, 120...
By examining the lists, we can see that the smallest number that appears in all three lists is 120. Therefore, the LCM of 5, 6, and 8 is 120.
While this method is easy to understand, it becomes less efficient when dealing with larger numbers. Imagine trying to find the LCM of 252, 378, and 504 using this method – it would be incredibly time-consuming! This highlights the need for more efficient methods.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Let's find the prime factorization of each number:
- 5: 5 (5 is a prime number)
- 6: 2 x 3
- 8: 2 x 2 x 2 = 2³
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together: 8 x 3 x 5 = 120. Therefore, the LCM of 5, 6, and 8 is 120.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b) = (a x b) / GCD(a, b)
This formula can be extended to more than two numbers. However, calculating the GCD for multiple numbers requires a slightly more complex approach, often using the Euclidean algorithm. Let's illustrate this with our example:
First, we need to find the GCD of 5, 6, and 8. Since 5 is a prime number and doesn't divide into 6 or 8, the GCD(5, 6, 8) = 1.
While this particular example is straightforward, finding the GCD of larger numbers requires iterative application of the Euclidean Algorithm or similar techniques.
Now, applying the formula (although not strictly applicable in its simplest form to three numbers directly), we can understand the relationship. The LCM will be a multiple that incorporates all the prime factors of each number. Since the GCD of 5, 6 and 8 is 1, their LCM is simply the product of the three numbers, which contains all the prime factors in their highest powers as we've already established. However, for multiple numbers, it's advisable to stick with prime factorisation for simplicity and better insight.
Illustrative Examples and Applications
The concept of LCM has practical applications in various fields. Let’s explore a few examples:
-
Scheduling: Imagine you have three different events happening on a recurring basis. Event A happens every 5 days, Event B every 6 days, and Event C every 8 days. To find the next time all three events will coincide, you need to find the LCM(5, 6, 8) = 120. Therefore, all three events will occur together again in 120 days.
-
Fraction Addition and Subtraction: When adding or subtracting fractions, you need a common denominator. This common denominator is usually the LCM of the denominators. For example, to add 1/5 + 1/6 + 1/8, you would find the LCM of 5, 6, and 8 (which is 120), and convert each fraction to have a denominator of 120 before performing the addition.
-
Gear Ratios and Mechanical Systems: In mechanical engineering, LCM is used to determine gear ratios and synchronize the rotations of multiple gears in a system.
-
Cyclic Processes: In numerous scientific and engineering problems involving cyclical processes (like waves, oscillations, or periodic events), finding the LCM helps determine when these cycles will align or overlap.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for a set of numbers?
A: Yes, there is only one least common multiple for any given set of numbers.
Q: What if one of the numbers is 0?
A: The LCM is undefined when one or more of the numbers is 0.
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have built-in functions to calculate the LCM. You can also find numerous online calculators that can perform this calculation. However, understanding the underlying methods is essential for solving more complex problems.
Conclusion
Finding the LCM of 5, 6, and 8, as demonstrated through different methods, isn't just about arriving at the answer (120). It’s about developing a deeper understanding of the fundamental concepts of multiples, prime factorization, and the relationship between LCM and GCD. These concepts extend far beyond simple arithmetic exercises, forming the bedrock of more advanced mathematical topics and practical applications in various fields. Master these methods and you will be well-equipped to tackle more challenging problems involving multiples and divisors. Remember, practice is key to solidifying your understanding and improving your efficiency in calculating LCMs. Work through different examples, experimenting with the various methods outlined here, and you'll find yourself confidently tackling any LCM problem that comes your way.
Latest Posts
Latest Posts
-
What Percent Is 5 8
Sep 15, 2025
-
6 To The Fifth Power
Sep 15, 2025
-
Lcm Of 14 And 16
Sep 15, 2025
-
Lcm Of 3 9 15
Sep 15, 2025
-
12 15 In Simplest Form
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.