Lcm Of 15 And 8
saludintensiva
Sep 17, 2025 · 7 min read
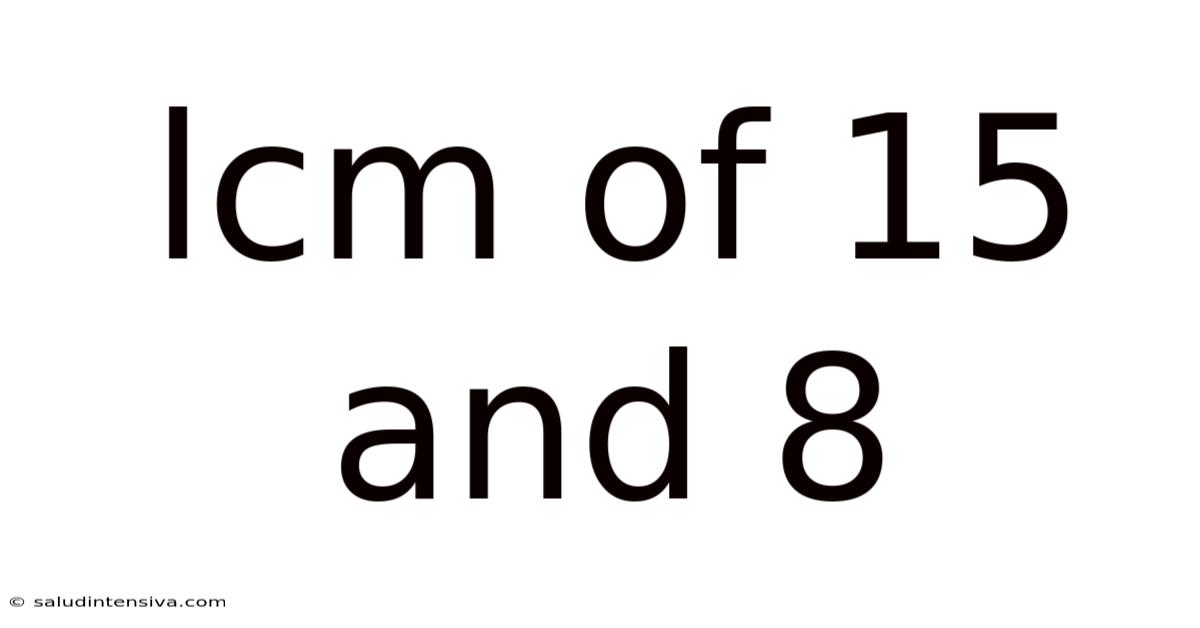
Table of Contents
Finding the Least Common Multiple (LCM) of 15 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide delves into the process of finding the LCM of 15 and 8, exploring various techniques and providing a deeper understanding of this fundamental concept in number theory. We'll go beyond a simple answer and explore why LCM is important, different calculation methods, and even touch on related concepts like the greatest common divisor (GCD). This will ensure you not only know the answer but also fully grasp the 'why' behind the calculations.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events.
For instance, imagine you have two gears, one rotating every 15 seconds and the other every 8 seconds. Finding the LCM of 15 and 8 will tell you when both gears will simultaneously be at their starting positions again. This concept extends beyond simple gears; it's applied in scheduling, music theory (finding the least common denominator for rhythmic patterns), and much more.
This article will focus on finding the LCM of 15 and 8, showcasing multiple methods to achieve the result and strengthening your understanding of the concept.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 120. Therefore, the LCM of 15 and 8 is 120.
This method works well for smaller numbers, but it becomes increasingly inefficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 15: 3 x 5
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2³ = 8.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together gives us the LCM: 8 x 3 x 5 = 120.
Method 3: Using the Formula Involving GCD
The least common multiple (LCM) and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two integers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, we need to find the GCD of 15 and 8. The GCD is the largest number that divides both 15 and 8 without leaving a remainder. In this case, the GCD(15, 8) = 1 because 15 and 8 share no common factors other than 1.
Now, we can apply the formula:
LCM(15, 8) = (15 x 8) / 1 = 120
Method 4: Ladder Method (Division Method)
The ladder method, also known as the division method, is another efficient way to find the LCM, particularly useful when dealing with three or more numbers. This method uses successive divisions by prime numbers.
-
Arrange the numbers in a row: 15 8
-
Divide by the smallest prime number that divides at least one of the numbers. In this case, it's 2:
2 | 15 8 | 15 4
-
Continue dividing by the smallest prime number that divides at least one of the remaining numbers until all the numbers become 1:
2 | 15 4 | 15 2 3 | 15 1 | 5 1 5 | 5 1 | 1 1
-
Multiply all the prime numbers used in the division and the remaining numbers (which are all 1s in this case): 2 x 2 x 3 x 5 = 120
Why Learn Different Methods?
While all methods lead to the same result (120 in this case), learning multiple approaches offers several advantages:
- Versatility: Different methods are more efficient for different types of numbers. The listing method is quick for small numbers, while prime factorization and the ladder method handle larger numbers more effectively.
- Conceptual Understanding: Each method sheds light on a different aspect of LCM. Prime factorization highlights the fundamental building blocks of numbers, while the GCD method reveals the relationship between LCM and GCD.
- Problem-Solving Skills: Mastering multiple methods enhances your overall mathematical problem-solving skills, equipping you to tackle various challenges with greater confidence.
Further Exploration: Applications of LCM
The LCM has numerous applications beyond the simple examples mentioned earlier:
- Fraction Addition and Subtraction: Finding a common denominator for adding or subtracting fractions requires finding the LCM of the denominators.
- Cyclic Events: Determining when events that repeat at regular intervals will coincide (like the gear example).
- Scheduling: Planning schedules for events that occur at different frequencies (e.g., meetings, deliveries).
- Music Theory: Calculating the least common denominator for rhythmic patterns to determine when they will align.
- Modular Arithmetic: LCM plays a critical role in solving congruences and other problems in modular arithmetic.
Understanding LCM isn't merely about memorizing a formula; it's about understanding the fundamental relationships between numbers and applying this knowledge to solve a variety of real-world problems.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both given numbers. The GCD (Greatest Common Divisor) is the largest number that divides both given numbers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases, and vice-versa.
Q: Can the LCM of two numbers be smaller than one of the numbers?
A: No. The LCM is always greater than or equal to the larger of the two numbers.
Q: What if I have more than two numbers? How do I find the LCM?
A: The prime factorization method and the ladder method work well for finding the LCM of more than two numbers. You would extend the process by including all the numbers in the factorization or division steps.
Q: Is there a way to calculate the LCM using a calculator?
A: Many scientific calculators have a built-in function to calculate the LCM (often denoted as LCM or LCD). However, understanding the methods described above is crucial for grasping the underlying mathematical concepts.
Conclusion
Finding the least common multiple of 15 and 8, as demonstrated through various methods, is more than just a simple calculation. It provides a valuable opportunity to enhance your understanding of fundamental number theory concepts. By mastering different approaches, you develop a deeper appreciation for the interconnectedness of mathematical ideas and gain valuable problem-solving skills applicable to a wide range of scenarios. Remember, the key is not only to find the answer (which is 120) but also to understand the why behind the calculations and the broader applications of the LCM in various fields. The journey of learning is as important as the destination itself!
Latest Posts
Latest Posts
-
2 10 As A Percent
Sep 17, 2025
-
4 4 5 As A Decimal
Sep 17, 2025
-
12 Out Of 16 Percentage
Sep 17, 2025
-
General Form To Standard Form
Sep 17, 2025
-
10 Out Of 16 Percentage
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.