Lcm Of 16 And 6
saludintensiva
Sep 10, 2025 · 6 min read
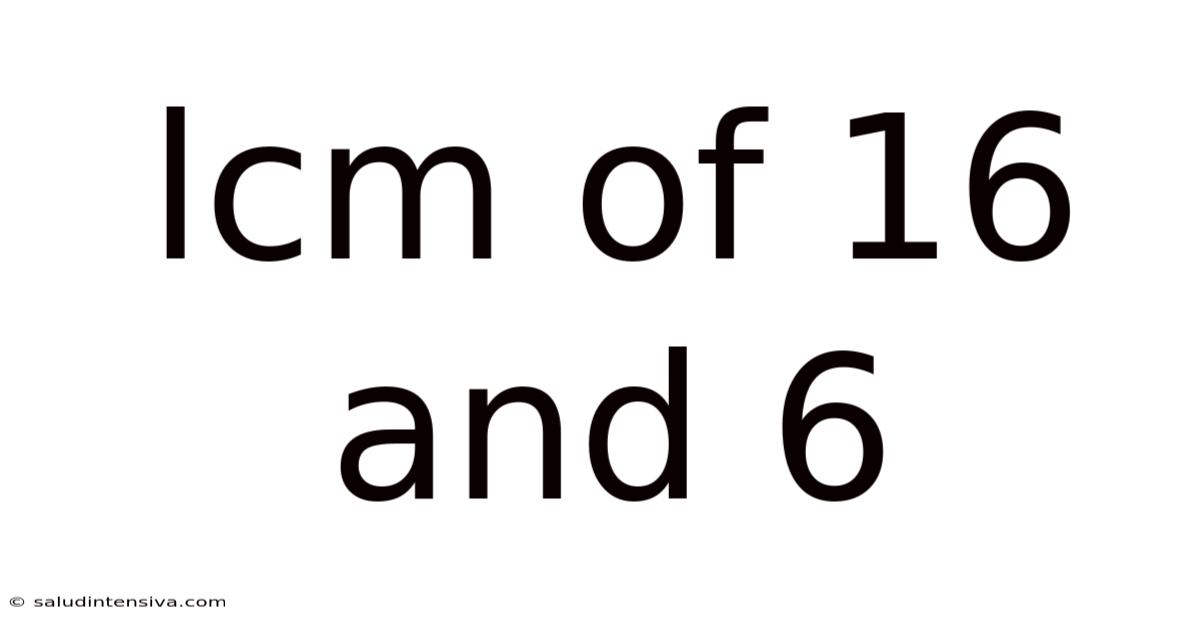
Table of Contents
Finding the Least Common Multiple (LCM) of 16 and 6: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a solid foundation in mathematics. This comprehensive guide will delve into the LCM of 16 and 6, explaining multiple approaches, exploring the theoretical background, and providing practical applications. We'll cover everything from basic prime factorization to more advanced techniques, ensuring you grasp the concept thoroughly.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. Understanding LCM is essential in various mathematical applications, from solving fractional equations to understanding rhythmic patterns in music. This article will specifically focus on finding the LCM of 16 and 6, demonstrating different methods to achieve this.
Method 1: Prime Factorization
This is a fundamental and widely used method for finding the LCM. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 16
16 can be factored as follows:
16 = 2 x 8 = 2 x 2 x 4 = 2 x 2 x 2 x 2 = 2<sup>4</sup>
Step 2: Prime Factorization of 6
6 can be factored as follows:
6 = 2 x 3
Step 3: Identifying Common and Uncommon Factors
Comparing the prime factorizations, we see that both numbers share one factor of 2. However, 16 has four factors of 2, and 6 has one factor of 3 that 16 lacks.
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together.
LCM(16, 6) = 2<sup>4</sup> x 3 = 16 x 3 = 48
Therefore, the least common multiple of 16 and 6 is 48.
Method 2: Listing Multiples
This method is simpler for smaller numbers but becomes less efficient for larger ones. It involves listing the multiples of each number until a common multiple is found.
Step 1: Listing Multiples of 16
Multiples of 16: 16, 32, 48, 64, 80, 96, ...
Step 2: Listing Multiples of 6
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, ...
Step 3: Identifying the Least Common Multiple
By comparing the lists, we can see that the smallest common multiple of 16 and 6 is 48. This confirms the result obtained through prime factorization.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
Step 1: Finding the GCD of 16 and 6
We can use the Euclidean algorithm to find the GCD.
- Divide 16 by 6: 16 = 2 x 6 + 4
- Divide 6 by the remainder 4: 6 = 1 x 4 + 2
- Divide 4 by the remainder 2: 4 = 2 x 2 + 0
The last non-zero remainder is 2, so the GCD(16, 6) = 2.
Step 2: Calculating the LCM using the formula
LCM(16, 6) = (16 x 6) / GCD(16, 6) = (96) / 2 = 48
This method again confirms that the LCM of 16 and 6 is 48.
Understanding the Concept of Divisibility
The concept of divisibility is fundamental to understanding LCM. A number 'a' is divisible by another number 'b' if the division of 'a' by 'b' results in a whole number (no remainder). In the context of LCM, we are looking for the smallest number that is divisible by both 16 and 6.
Practical Applications of LCM
The LCM has numerous practical applications across various fields:
- Scheduling: Determining when two cyclical events will occur simultaneously (e.g., two buses arriving at a stop at different intervals).
- Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
- Music: Understanding rhythmic patterns and finding the least common multiple of note durations.
- Construction/Engineering: Calculating optimal lengths or measurements for projects involving repeating patterns or cycles.
- Computer Science: Synchronization of processes and tasks within computer systems.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all the prime factors of all the numbers involved. For the listing method, you need to list multiples of all numbers until a common multiple is found. The GCD method can also be extended using more sophisticated algorithms for finding the GCD of multiple numbers.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They represent opposite ends of the divisibility spectrum for a given set of numbers.
Q2: Can the LCM of two numbers be one of the numbers?
Yes, this occurs when one number is a multiple of the other. For example, LCM(4, 8) = 8.
Q3: Is there a formula to directly calculate the LCM without using prime factorization or the GCD?
While there isn't a single, universally applicable direct formula, iterative methods can be used to find the LCM. These methods often involve checking multiples sequentially until a common multiple is found.
Q4: How can I use LCM to add fractions?
To add fractions with different denominators, find the LCM of the denominators (this is the LCD). Convert each fraction to an equivalent fraction with the LCD as the denominator. Then, add the numerators and keep the LCD as the denominator.
Q5: Why is prime factorization important in finding the LCM?
Prime factorization provides a systematic way to break down numbers into their fundamental building blocks. By examining the prime factors, we can easily identify the highest power of each prime factor present in the numbers, which is crucial for calculating the LCM.
Conclusion
Finding the least common multiple of 16 and 6, which is 48, is a straightforward process once the underlying concepts are understood. We explored three different methods – prime factorization, listing multiples, and using the GCD – each providing a valuable approach to solving this type of problem. The LCM, though seemingly a simple concept, plays a significant role in various mathematical applications and demonstrates the interconnectedness of different mathematical ideas. By mastering the calculation of LCM, you'll enhance your mathematical skills and gain a deeper appreciation for the elegance and practicality of number theory. Remember to practice these methods with different numbers to solidify your understanding and build your problem-solving abilities.
Latest Posts
Latest Posts
-
What Is Half Of 78
Sep 10, 2025
-
Lcm Of 4 And 30
Sep 10, 2025
-
5 Root 3 Whole Square
Sep 10, 2025
-
5 1 2 As A Decimal
Sep 10, 2025
-
11 2 As A Mixed Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 16 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.