Lcm Of 25 And 4
saludintensiva
Sep 14, 2025 · 5 min read
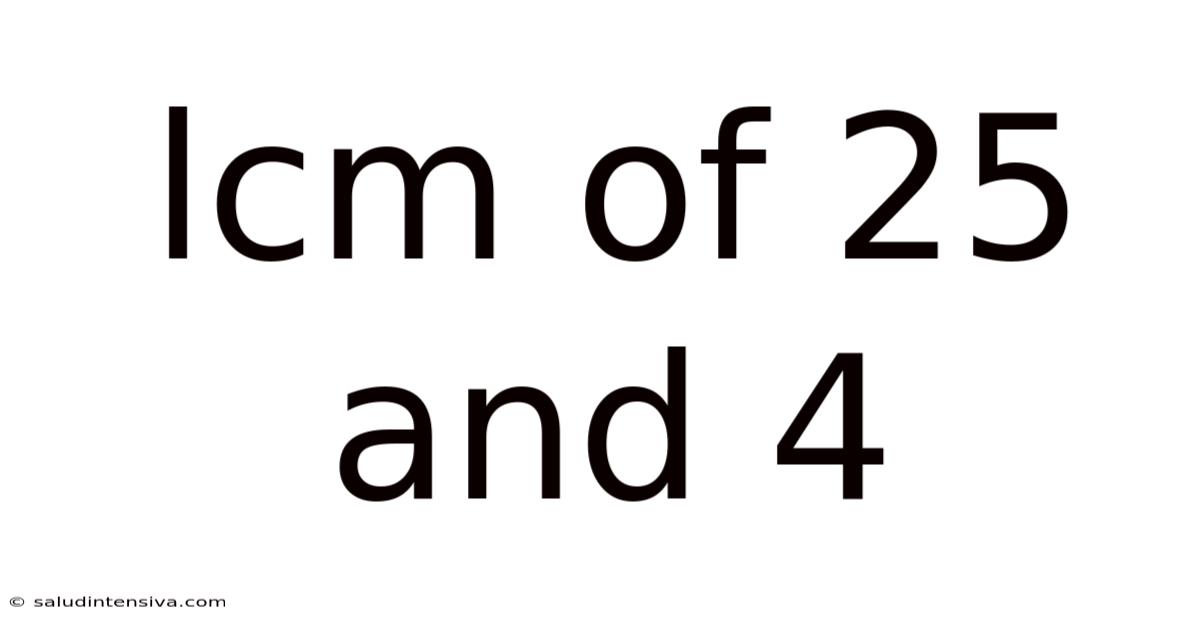
Table of Contents
Understanding the Least Common Multiple (LCM) of 25 and 4
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts is crucial for grasping more advanced mathematical concepts. This article delves deep into calculating the LCM of 25 and 4, exploring various methods, explaining the underlying mathematical principles, and addressing frequently asked questions. By the end, you'll not only know the LCM of 25 and 4 but also possess a solid understanding of how to find the LCM of any two numbers. This comprehensive guide will be beneficial for students of all levels, from elementary school to high school, and even serve as a helpful refresher for adults.
Introduction to Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Think of it like finding the smallest common ground between different sets of multiples. Understanding LCM is essential in various mathematical applications, including solving problems involving fractions, ratios, and scheduling.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this method to find the LCM of 25 and 4.
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, ...
By comparing the lists, we can see that 100 is the smallest number that appears in both lists. Therefore, the LCM of 25 and 4 is 100. This method is simple for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is using prime factorization. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). Let's break down 25 and 4 into their prime factors:
- 25: 5 x 5 = 5²
- 4: 2 x 2 = 2²
Now, to find the LCM, we take the highest power of each prime factor present in the numbers and multiply them together:
- The prime factors are 2 and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 5 is 5² = 25.
- LCM(25, 4) = 2² x 5² = 4 x 25 = 100
This method is more systematic and less prone to errors, making it ideal for larger numbers.
Method 3: Using the Formula (LCM and GCD Relationship)
The LCM and the Greatest Common Divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. First, we need to find the GCD of 25 and 4. The GCD is the largest number that divides both 25 and 4 without leaving a remainder. In this case, the GCD(25, 4) = 1, as 1 is the only common divisor.
Now, we can use the formula:
LCM(25, 4) x GCD(25, 4) = 25 x 4 LCM(25, 4) x 1 = 100 LCM(25, 4) = 100
Understanding the Mathematical Principles Behind LCM
The LCM is fundamentally related to the concept of divisibility. When a number is divisible by another, it means that the division results in a whole number without any remainder. The LCM represents the smallest number that satisfies the divisibility condition for all the numbers involved. The prime factorization method highlights this concept effectively, as it shows the fundamental building blocks (prime factors) that make up the numbers. By combining the highest powers of each prime factor, we ensure that the resulting LCM is divisible by all the original numbers.
Applications of LCM in Real-World Scenarios
The LCM finds practical applications in various real-world scenarios:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously.
- Fraction Operations: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator for easier calculations.
- Pattern Recognition: The LCM helps identify repeating patterns in sequences of numbers or events.
- Measurement Conversions: Converting between different units of measurement often involves using the LCM to find a common multiple.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have common factors?
A1: The prime factorization method handles common factors efficiently. The formula method also implicitly accounts for common factors through the GCD calculation.
Q2: Is there a difference between LCM and GCD?
A2: Yes. The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related but represent opposite ends of the divisibility spectrum.
Q3: Can the LCM be larger than the numbers themselves?
A3: Yes, the LCM is often larger than the individual numbers, except in cases where one number is a multiple of the other.
Q4: What if I have more than two numbers?
A4: The same principles apply. For more than two numbers, you can extend the prime factorization method or use iterative approaches involving the pairwise LCM calculations.
Q5: Are there any other methods for finding LCM?
A5: Yes, there are more advanced algorithms and techniques for finding the LCM, particularly efficient for very large numbers. However, the methods explained above are sufficient for most practical purposes.
Conclusion: Mastering the LCM
Finding the LCM, whether it's for 25 and 4 or any other pair of numbers, is a fundamental skill in mathematics. Understanding the different methods – listing multiples, prime factorization, and using the LCM-GCD relationship – provides a strong foundation for tackling more complex mathematical problems. The applications of LCM extend far beyond simple arithmetic exercises; they are crucial for solving problems in various fields. By mastering the LCM, you equip yourself with a powerful tool for understanding and solving real-world mathematical challenges. Remember, the key is to choose the method that best suits the numbers involved and your comfort level with different mathematical techniques. Practice consistently, and you'll find calculating the LCM becomes second nature.
Latest Posts
Latest Posts
-
2 2 8 As A Decimal
Sep 14, 2025
-
90 Percent As A Decimal
Sep 14, 2025
-
Convert 7 To A Decimal
Sep 14, 2025
-
6 5 M 1 26
Sep 14, 2025
-
Whats Equivalent To 2 4
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 25 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.