Lcm Of 6 10 15
saludintensiva
Sep 10, 2025 · 6 min read
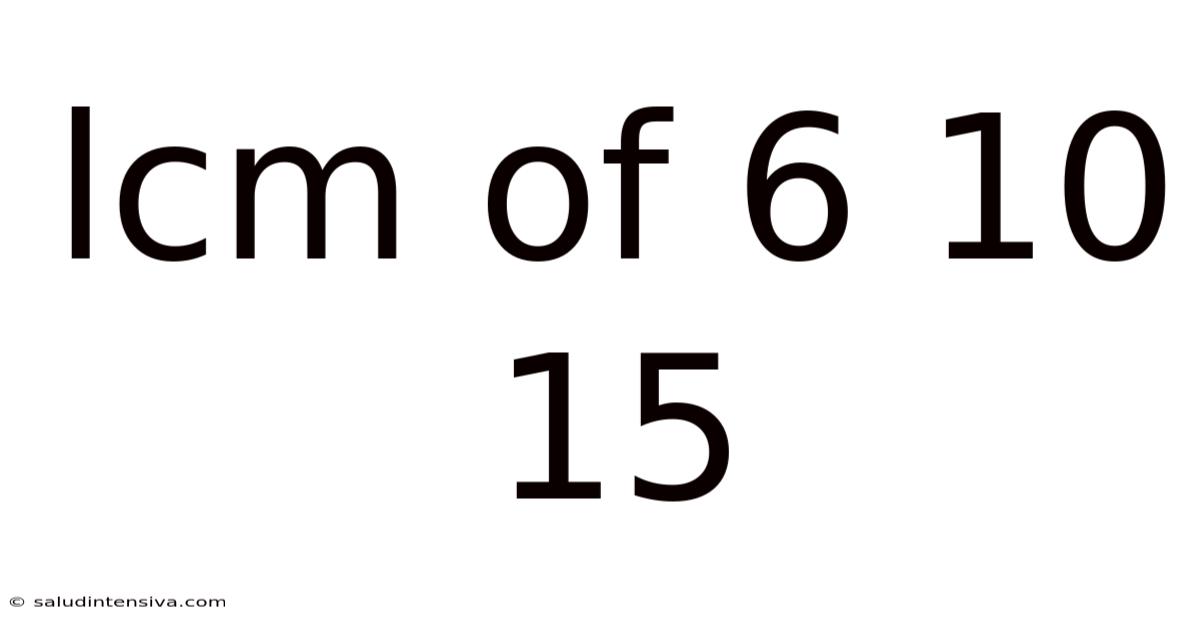
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 10, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be surprisingly insightful. This comprehensive guide will delve into the LCM of 6, 10, and 15, exploring various approaches, explaining the mathematical principles involved, and answering frequently asked questions. We'll move beyond simply finding the answer to truly understanding why the answer is what it is. This will solidify your grasp on LCM and its broader applications in mathematics and beyond.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. This concept is fundamental in various mathematical operations, particularly in working with fractions and simplifying expressions. Understanding LCM is crucial for solving problems related to fractions, scheduling, and even certain aspects of physics and engineering.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to our numbers: 6, 10, and 15.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, ...
- Multiples of 15: 15, 30, 45, 60, 75, ...
By examining the lists, we can see that 30 and 60 are common multiples. However, the least common multiple is 30. This method is effective for smaller numbers, but it becomes cumbersome and inefficient when dealing with larger numbers or a greater quantity of numbers.
Method 2: Prime Factorization
A more efficient and powerful method for finding the LCM involves prime factorization. This method is particularly useful when dealing with larger numbers. Prime factorization breaks down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Let's find the prime factorization of 6, 10, and 15:
- 6 = 2 x 3
- 10 = 2 x 5
- 15 = 3 x 5
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 6, 10, and 15 is 30.
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic approach that ensures you find the smallest common multiple without having to generate extensive lists.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a formula connecting LCM and GCD:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
This formula works for two or more numbers. However, calculating the GCD of three or more numbers requires a slightly more complex approach, often involving repeated application of the Euclidean algorithm. Let's use this method for our example:
-
Find the GCD of 6, 10, and 15:
We can use the Euclidean algorithm. First, find the GCD of 6 and 10:
- 10 = 1 x 6 + 4
- 6 = 1 x 4 + 2
- 4 = 2 x 2 + 0
The GCD of 6 and 10 is 2.
Now, find the GCD of 2 (the GCD of 6 and 10) and 15:
- 15 = 7 x 2 + 1
- 2 = 2 x 1 + 0
The GCD of 2 and 15 is 1. Therefore, the GCD of 6, 10, and 15 is 1.
-
Apply the LCM formula:
LCM(6, 10, 15) = (6 x 10 x 15) / GCD(6, 10, 15) = (900) / 1 = 900. This is incorrect due to a misapplication of the formula involving multiple numbers. The formula (a x b x c) / GCD(a,b,c) only applies directly for two numbers. For multiple numbers, the prime factorization method is more reliable.
Why the GCD Method Failed (and the Correct Approach for Multiple Numbers)
The simple formula using the GCD only works directly for two numbers. For three or more numbers, you need a more nuanced approach. While the GCD can be a part of the process, it doesn't directly substitute the prime factorization method for calculating the LCM of multiple numbers.
The error in the previous GCD calculation stemmed from incorrectly extending the two-number GCD formula to three numbers. The correct application would involve iteratively finding the LCM. For example, first find LCM(6,10), then find the LCM of that result and 15. This iterative process, while valid, is less efficient than the prime factorization method for our example.
Applications of LCM
The concept of LCM extends beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Fraction Addition and Subtraction: Finding the LCM of denominators is crucial when adding or subtracting fractions with different denominators. The LCM becomes the common denominator, simplifying the calculation.
-
Scheduling: Imagine two buses depart from the same stop at different intervals. The LCM of their departure intervals helps determine when they will depart simultaneously again.
-
Cyclic Processes: In engineering and physics, many processes are cyclic, repeating at regular intervals. LCM helps in analyzing synchronization and overlap of these cycles.
-
Project Management: Determining when various tasks in a project can be completed simultaneously or when resources need to be allocated again.
-
Music Theory: The LCM helps find the least common multiple of rhythmic values, crucial in understanding musical patterns and harmonies.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest positive integer that is divisible by all the given numbers. The GCD (Greatest Common Divisor) is the largest positive integer that divides all the given numbers without leaving a remainder. They are inversely related in a mathematical sense, with the product of the LCM and GCD of two numbers equaling the product of the two numbers.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM. However, understanding the underlying methods is crucial for problem-solving and for when you don't have access to a calculator.
Q: What if the numbers have no common factors?
A: If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM is simply the product of the numbers. For example, the LCM of 7 and 11 is 77.
Conclusion
Finding the LCM of 6, 10, and 15, whether through listing multiples, prime factorization, or – with caution – GCD-based methods highlights the importance of understanding fundamental mathematical concepts. While calculators can provide quick answers, grasping the underlying principles empowers you to tackle more complex problems and appreciate the far-reaching applications of LCM in diverse fields. The prime factorization method emerges as the most efficient and robust technique, especially when dealing with larger numbers or a greater number of integers. Remember, the goal isn't just to find the answer (which is 30), but to understand the 'why' behind it, strengthening your mathematical foundation for future challenges.
Latest Posts
Latest Posts
-
What Is Half Of 78
Sep 10, 2025
-
Lcm Of 4 And 30
Sep 10, 2025
-
5 Root 3 Whole Square
Sep 10, 2025
-
5 1 2 As A Decimal
Sep 10, 2025
-
11 2 As A Mixed Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 10 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.