Lcm Of 6 9 12
saludintensiva
Sep 19, 2025 · 6 min read
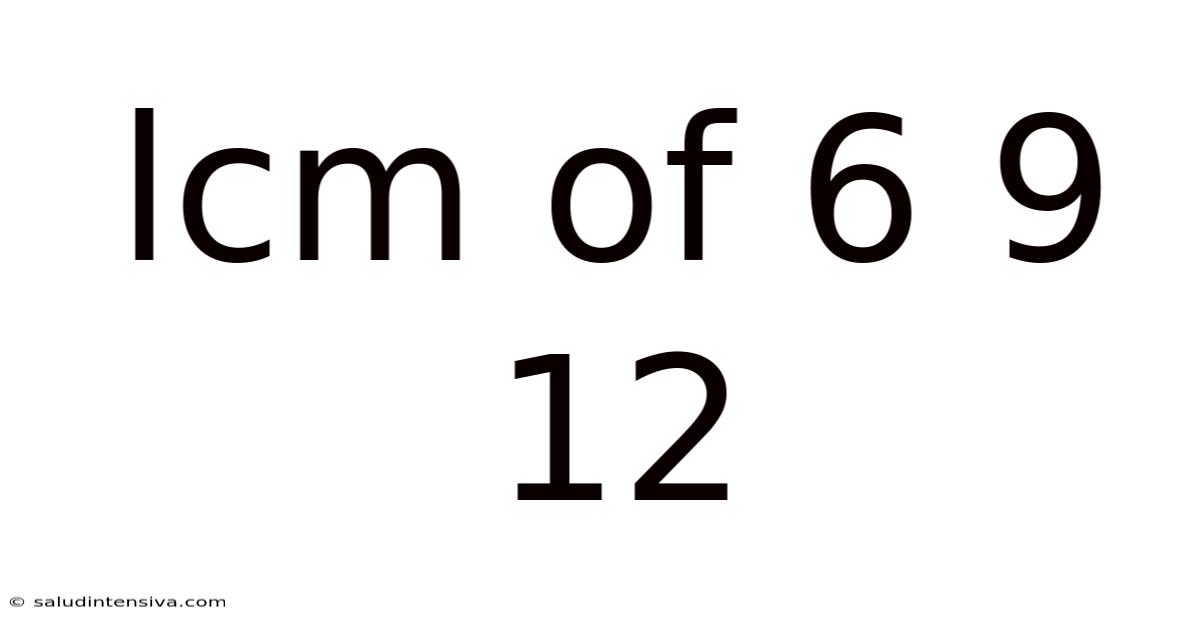
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 9, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for solving various problems in arithmetic, algebra, and even real-world scenarios involving timing and scheduling. This article will provide a thorough explanation of how to find the LCM of 6, 9, and 12, exploring different methods and delving into the underlying mathematical principles. We'll move beyond a simple answer and explore the "why" behind the calculations, ensuring a deep understanding of the concept.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding LCM is vital in various applications, from simplifying fractions to solving problems involving cyclical events, such as determining when several events will occur simultaneously. This article focuses on finding the LCM of 6, 9, and 12, demonstrating several approaches and solidifying your understanding of this important mathematical concept.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is listing the multiples of each number until you find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
By comparing the lists, we can see that the smallest number appearing in all three lists is 36. Therefore, the LCM of 6, 9, and 12 is 36.
This method is simple to visualize but can become cumbersome with larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
Now, multiply these highest powers together: 4 x 9 = 36. Thus, the LCM of 6, 9, and 12 is 36.
This method is systematic and efficient, even for larger numbers, making it a preferred method for more complex LCM problems.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This formula can be extended to more than two numbers, although the calculation becomes slightly more involved. First, let's find the GCD of 6, 9, and 12. We can use the Euclidean algorithm for this:
-
Find the GCD of 6 and 9:
- 9 = 1 * 6 + 3
- 6 = 2 * 3 + 0
- The GCD of 6 and 9 is 3.
-
Find the GCD of 3 and 12:
- 12 = 4 * 3 + 0
- The GCD of 3 and 12 is 3.
Therefore, the GCD of 6, 9, and 12 is 3. However, this method is less straightforward for finding the LCM directly when dealing with three or more numbers. While the relationship between GCD and LCM is mathematically significant, directly applying the formula to find the LCM of three or more numbers requires careful consideration of the GCD for each pair and is generally less efficient than prime factorization in this scenario.
Method 4: Using the Ladder Method (or Prime Factorization visualized)
This method provides a visual approach to prime factorization, making it easier to understand, especially for beginners. Let's illustrate it:
2 | 6 9 12
3 | 3 9 6
| 1 3 2
We start by dividing all three numbers by the smallest prime number that divides at least one of them (2 in this case). We repeat this process with the next smallest prime number (3) until we reach 1 for all numbers. The LCM is then the product of all the prime numbers used: 2 x 3 x 3 x 2 = 36. This method combines the efficiency of prime factorization with a clear visual representation.
Explanation of the LCM in the Context of 6, 9, and 12
The LCM of 6, 9, and 12, which is 36, signifies the smallest number that is a multiple of all three. This means that 36 can be divided evenly by 6, 9, and 12 without leaving a remainder. Consider scenarios where understanding LCM is crucial:
-
Scheduling: Imagine three events occurring at intervals of 6, 9, and 12 minutes. The LCM (36) represents the time when all three events will coincide again.
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential for finding a common denominator, simplifying the calculation.
-
Pattern Recognition: The LCM can help identify repeating patterns in sequences.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor (the largest number that divides all the given numbers).
-
Can the LCM be larger than the largest number in the set? Yes, the LCM is often larger than the largest number in the set, as seen in our example (36 > 12).
-
Is there only one LCM for a set of numbers? Yes, there's only one least common multiple for a given set of numbers.
-
What if one of the numbers is zero? The LCM of any set of numbers containing zero is undefined.
-
How can I calculate the LCM of more than three numbers? The prime factorization method remains the most efficient approach. Find the prime factorization of each number, and take the highest power of each prime factor present. Then multiply these highest powers together to obtain the LCM. The ladder method can be adapted for more numbers as well.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill in mathematics with various practical applications. While the simple listing method works for small numbers, the prime factorization method (and its visual equivalent, the ladder method) offers a more efficient and robust approach for larger numbers and more complex problems. Understanding the concepts of prime factorization and the relationship between LCM and GCD provides a solid foundation for tackling more advanced mathematical concepts. Mastering LCM calculations enhances your problem-solving skills and opens doors to a deeper understanding of number theory and its applications in various fields. Through the examples and explanations provided, you now possess the tools and understanding to confidently calculate the LCM of any set of numbers and appreciate its significance within the broader landscape of mathematics.
Latest Posts
Latest Posts
-
6 1 4 In Decimal
Sep 19, 2025
-
1 11 As A Percent
Sep 19, 2025
-
21 16 As A Mixed Number
Sep 19, 2025
-
Simplest Form Of 5 15
Sep 19, 2025
-
9 40 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 9 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.