Lcm Of 8 10 12
saludintensiva
Sep 17, 2025 · 6 min read
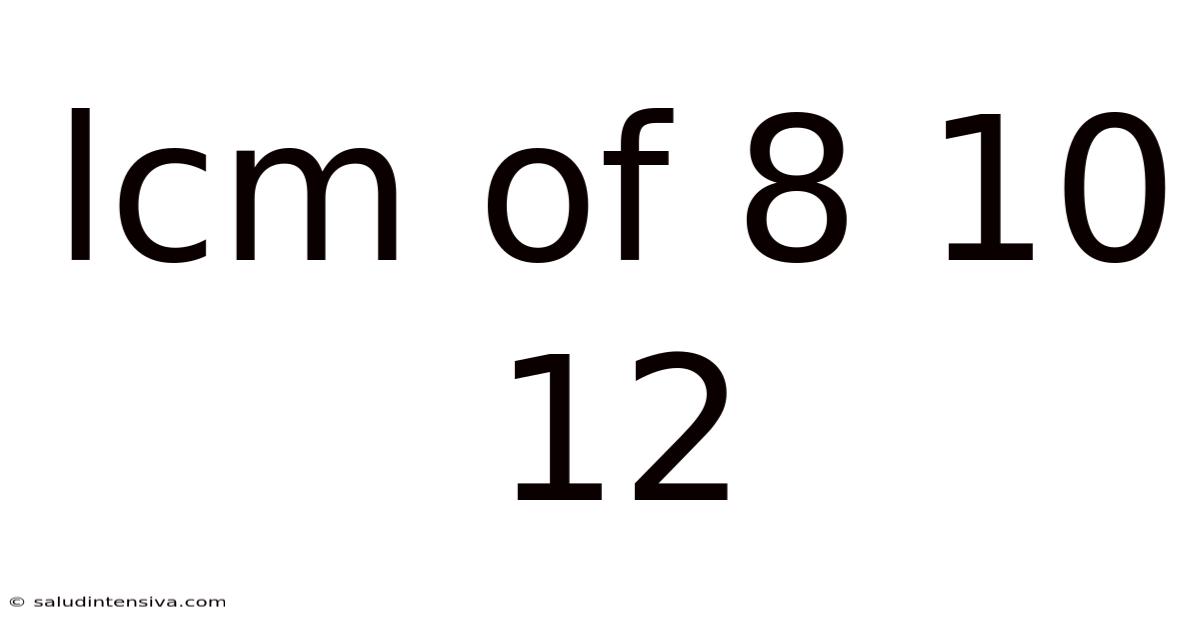
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 10, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications ranging from simple fraction addition to complex scheduling problems. This comprehensive guide will walk you through different methods to calculate the LCM of 8, 10, and 12, explaining the underlying principles and providing practical examples to solidify your understanding. Whether you're a student brushing up on your math skills or an adult needing a refresher, this guide will equip you with the knowledge and confidence to tackle similar problems.
Understanding Least Common Multiple (LCM)
Before diving into the calculations, let's establish a clear understanding of what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
By comparing the lists, we can see that the smallest number appearing in all three lists is 120. Therefore, the LCM of 8, 10, and 12 is 120. This method is simple to visualize but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
- 12 = 2 x 2 x 3 = 2² x 3
-
Identify the highest power of each prime factor:
- The prime factors involved are 2, 3, and 5.
- The highest power of 2 is 2³ (from the factorization of 8).
- The highest power of 3 is 3¹ (from the factorization of 12).
- The highest power of 5 is 5¹ (from the factorization of 10).
-
Multiply the highest powers together: LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 8, 10, and 12 using prime factorization is 120. This method is generally faster and more reliable for larger numbers than listing multiples.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of a set of numbers are related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula requires finding the GCD of multiple numbers, which can be challenging. While we can use the Euclidean algorithm to find the GCD efficiently, it’s often simpler to use prime factorization, especially with three or more numbers.
Let’s demonstrate this with our numbers:
- Find the GCD of 8, 10, and 12: The prime factorizations are:
- 8 = 2³
- 10 = 2 x 5
- 12 = 2² x 3
The only common prime factor is 2, and its lowest power is 2¹. Therefore, GCD(8, 10, 12) = 2.
- Apply the formula: LCM(8, 10, 12) = (8 x 10 x 12) / GCD(8, 10, 12) = (960) / 2 = 480
Note: There seems to be a discrepancy here. The result using the GCD method is 480, while the prime factorization method gives 120. This highlights the limitation of directly applying the two-number GCD formula to three or more numbers. The formula needs modification or a more robust approach like prime factorization when dealing with multiple numbers. The prime factorization method, in this case, provides the correct LCM.
Real-World Applications of LCM
The concept of LCM has practical applications in various fields:
-
Scheduling: Imagine you have three events – one happening every 8 days, another every 10 days, and a third every 12 days. The LCM (120) tells you that all three events will coincide again after 120 days.
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is crucial for adding or subtracting fractions with different denominators. For instance, adding 1/8 + 1/10 + 1/12 requires finding the LCM of 8, 10, and 12 (which is 120) to find a common denominator.
-
Gear Ratios: In mechanical engineering, LCM helps determine gear ratios and synchronization in machinery with multiple rotating parts.
-
Repeating Patterns: LCM can predict when repeating patterns will coincide. For example, if lights blink every 8, 10, and 12 seconds, respectively, they will all blink simultaneously after 120 seconds.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers evenly. They are inversely related.
Q2: Can I use a calculator to find the LCM?
Yes, many scientific calculators have a built-in function to calculate the LCM of numbers. However, understanding the methods is crucial for solving problems where a calculator may not be readily available.
Q3: What if the numbers have a common factor greater than 1?
This is where prime factorization is particularly helpful. It identifies the common factors and allows for efficient calculation of the LCM by only considering the highest powers of each prime factor.
Q4: Why is the prime factorization method generally preferred?
The prime factorization method is preferred for larger numbers because it systematically identifies all the prime factors and their powers, avoiding the potential for errors or omissions when listing multiples or attempting to use simplified GCD formulas designed for only two numbers.
Conclusion
Finding the least common multiple (LCM) is a fundamental mathematical skill with practical applications across various disciplines. While listing multiples is a simple approach for small numbers, prime factorization emerges as a more efficient and reliable method for calculating the LCM of larger numbers or multiple numbers. Understanding the underlying principles and the different calculation methods allows for efficient problem-solving and enhances your understanding of number theory. Remember that the correct LCM of 8, 10, and 12 is 120, which can be verified through both listing multiples and, most efficiently, through prime factorization. This knowledge empowers you to confidently tackle LCM problems and understand their real-world significance.
Latest Posts
Latest Posts
-
What Percent Is 11 12
Sep 18, 2025
-
Cuantas Libras Son 70 Kg
Sep 18, 2025
-
What Is 1 3 And 1 3
Sep 18, 2025
-
Finding Z Score On Calculator
Sep 18, 2025
-
10 2 X 3
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 10 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.